Shotgun Pi
May 5, 2014
I've had an interest in the
mathematical constant,
pi, since I first learned of it in
elementary school. Since I've published a book about pi this year, it's apparent that this interest still holds. Although just a few digits of pi are required in any
scientific or practical
calculation, pi has been calculated to ten trillion (10
13) digits. I reviewed some simple
analytical and
physical methods of
estimating the value of pi in a
previous article (Another Piece of Pi, July 28, 2010).
The
observable universe is a
sphere with a
diameter of about 9 x 10
26 meters. This means that only 27 digits of pi are needed to calculate its
circumference to better than a meter. Since the size of a
hydrogen atom is about 100
picometer (10
-10 meter), only 37 digits of pi are needed to calculate the circumference of the universe to the size of an
atom.
The
fraction, 22/7, is a close
approximation to the value of pi, as
Archimedes discovered by
circumscribing polygons around a
circle, noting their
perimeter P, and taking a
ratio to the diameter
D of the circle to get π ≈ P/D. Archimedes obtained his estimate of 22/7 (3.142857...) for pi using a circumscribed 96-sided polygon.
Ptolemy improved Archimedes' estimate with a 360-sided polygon, obtaining 3,141666..., a value that's correct to three decimal places.

Sculpture of Archimedes by Gerhard Thieme, Güstrow, Germany, 1977-1978.
(2012 photograph by "Niteshift," via Wikimedia Commons.)
Certain
species of
millet have small, 2 mm diameter
seeds that approximate a
physical point. While the
mustard seed takes
center stage when talking about something small, the millet seed figured into a
paradox of the
Greek philosopher,
Zeno. The paradox, which has been interpreted in various ways, involves the fact that a single millet seed doesn't appear to make a sound when it falls, but a
bushel of millet seed does.
Somewhere in my reading of the
history of mathematics, I remember that millet seeds were employed as a method for estimating the value of pi. Alas, a previous article of mine is the only source for this that
Google finds. The method is easy, as the figure shows. You toss a handful of millet seed onto a drawing a circle inscribed in a square, then you count how many seeds have landed on the circle, and how many there are in total. The ratio of these numbers is an estimate of the ratio of the
area of the circle to the area of square, from which pi may be calculated.
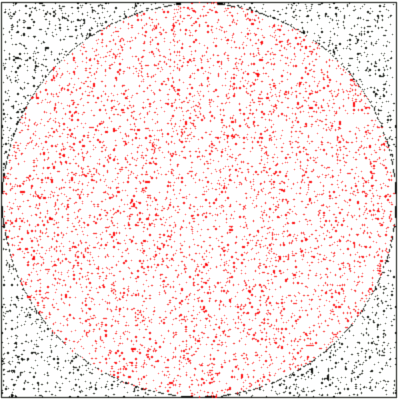
A square and an inscribed circle populated with random points to estimate pi.
I programmed this using Visual Basic more than twenty years ago)
The figure above was constructed using a
Visual Basic program. If a
graphical interface is not required, the
C programming language, or many other languages, will give better estimates, since you can "throw" many thousands of seeds many thousands of times. You can review my C
source code for this calculation,
here. As shown by the
histogram of results, 10,000 trials of 100,000 points/each gives us a
mean value of 3.1415697 with a
standard deviation of 0.00517947. This means that we're
95% certain that pi is between 3.1414587 and 3.1416613.
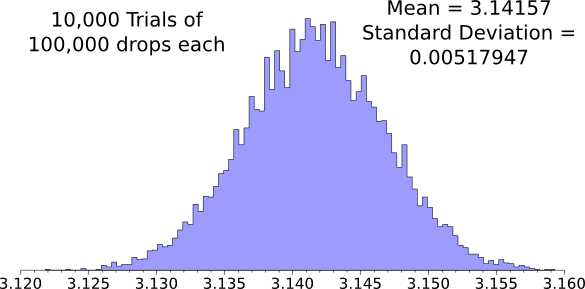
Histogram of the 'millet seed' method of estimating pi. (Graphed using Gnumeric.)
Vincent Dumoulin of the
Département d'informatique et de recherche opérationnelle of the
Université de Montréal and Félix Thouin of the
Département de physique, also of the Université de Montréal, have traded millet seeds for
shotgun pellets in a similar method for estimating pi.[1-2] Using a
Mossberg 500 pump-action shotgun, they determined an approximate value of 3.131 for pi, corresponding to a 0.33% error.
Perhaps
tongue-in-cheek, they observe that they're "...opening up new perspectives towards computing mathematical constants using everyday tools." They also write, "We feel confident that ballistic
Monte Carlo methods constitute reliable ways of computing mathematical constants should a tremendous
civilization collapse occur."
Their "calculation" involved firing the shotgun at a sheet of
aluminum foil at a twenty meter range. Careful
scientists as they are, they specify that the
shotgun cartridges had 3
dram-equivalents of
gunpowder and 32
grams of #8
lead pellets. The pellets are estimated to have an average
velocity of about 366
meters per second as they exit the gun. Firing 200 times resulted in 30,857
perforations. Multiple foils were used, and their results combined. The foils were
photographed and the hole locations were derived by
image analysis.[1-2]
Various physical factors such as the aim of the gun,
wind speed and direction, etc., will diminish the
randomness of the shot
distribution. To counter this, Dumoulin and Thouin used a random selection of the points (20,000) to
normalize the distribution, and they used the rest (10,000) to estimate pi.[1-2]
References:
- Vincent Dumoulin and Félix Thouin, "A Ballistic Monte Carlo Approximation of π," arXiv Preprint Server, April 8, 2014.
- How Mathematicians Used A Pump-Action Shotgun to Estimate Pi, The Physics arXiv Blog.
Permanent Link to this article
Linked Keywords: Mathematical constant; pi; elementary school; science; scientific; calculation; analytical; physics; physical; approximation; estimating; observable universe; sphere; diameter; meter; circumference; hydrogen atom; picometer; atom; fraction; approximation; Archimedes; tangential polygon; circumscribing; polygon; circle; perimeter; ratio; Ptolemy; Güstrow, Germany; Wikimedia Commons; species; millet; seed; physical point; mustard seed; Parable of the Mustard Seed; Zeno's paradoxes; Paradox of the Grain of Millet; paradox; Ancient Greek philosophy; Greek philosopher; Zeno of Elea; bushel; history of mathematics; Google Search; area; randomness; random; Visual Basic; gGraphical user interface; C programming language; source code; picalc.c; histogram; mean; standard deviation; confidence interval; 95% certainty; Gnumeric; Vincent Dumoulin; Département d'informatique et de recherche opérationnelle; Université de Montréal; Département de physique; shotgun shell; shotgun pellet; Mossberg 500; pump-action shotgun; tongue-in-cheek; Monte Carlo method; societal collapse; civilization collapse; aluminum foil; scientist; shotgun shell; shotgun cartridge; dram-equivalent; gunpowder; gram; lead; velocity; meters per second; perforation; digital photography; image analysis; wind speed; randomness; uniform distribution; normalization.