Disk Packing
January 29, 2024
One of my
uncles was a
Marine who
fought in World War II. After the war, he worked as a
welder and did things very interesting to my
youthful self. In the
1950s,
glass bottles were the
container of
choice for
soft drinks, and empty bottles has a small
bounty for their
return. In those days, there was no
city-wide recycling, and he would
roam the
neighborhood with an old
Radio Flyer wagon on the
night before
trash collection, finding
discarded bottles to be
exchanged for
cash.
He would also
roll his own
cigarettes, and I was fascinated by the
mechanical device that he used for that purpose. He also had a huge
glass jar of
coins that he would
sort, looking for some
rare coins that might be worth more than their
face value. I was reminded of this when I read about the discovery of a huge
cache of
ancient coins, some dating to 175
BC, at a
Japanese construction site about 70
miles outside of
Tokyo.[1] What most interested me was their arrangement in neat
stacks, quite unlike the
jumbled mass you would expect to find.

Unlike my uncle, I've never smoked. As this cartoon illustrates, smoking causes a financial burden as well as a health burden.
Governments have a financial interest in smoking cessation, since much of the expense of smoking-related health problems fall on them. One way governments discourage smoking, and also recoup health-related expenses, is through a cigarette tax.
George Harrison (1943-2001) of The Beatles had many health-related issues arising from smoking. These included throat cancer and lung cancer.
(Portion of Wellcome Trust Photo no. L0024904, Library ref., ICV No 51428, by Reginald Mount, via Wikimedia Commons. Click for larger image.)
One reason that
cigarettes are packed as twenty items is the
efficient stacking of 7, 6, and 7
cylinders.
Matchbooks also contain twenty
matches for the same reason. Another common packing is the
packing of spherical objects. The one obvious candidate for the
densest packing of identical spheres is the stacking used by
greengrocers when they stack
fruit. This
close-packing arrangement is shown in the figure.
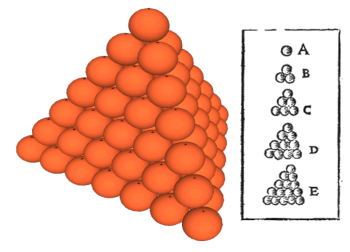
The well-known close-packing arrangement of spheres (right), along with the illustration that Johannes Kepler (1571-1630) used when making the conjecture that this is the densest possible arrangement.
(Left image by "Jvangiel," and right image from Johannes Kepler's 1611 Strena Seu de Nive Sexangula, both images via Wikimedia Commons. Click for larger image.)
Materials scientists and
crystallographers are familiar with this close packing of spheres, since this is the arrangement of
atoms in a
face-center-cubic crystal lattice, as found for such
metals as
aluminum and
copper. In this arrangement, and in all other close packings, each sphere
contacts twelve neighboring spheres. The average density in close packing is 0.74048; that is, nearly three-quarters of
space is filled.
In 1611,
Johannes Kepler (1571-1630) conjectured that this packing has the maximum possible density for all sphere packings, whether packed in a lattice, or packed in some irregular arrangement. In 1831,
Carl Friedrich Gauss (1777-1855) proved the conjecture for lattice packing, but it wasn't until 1998 that a
computer-assisted proof by
Thomas Hales (b. 1958) showed that an irregular packing couldn't do better.[2] Since this was a computer-assisted proof, verification of the proof was not easy, and it wasn't verified until 2014.[3]
Randomly packed spheres have a density of about 64%, quite a bit less than the 74% for close-packed lattice packing. In 2004,
physicist,
Paul Chaikin, and
chemist,
Salvatore Torquato, found that randomly packed
oblate spheroids have a higher density. A physical example of an oblate spheroid is an
M&M candy, and these will randomly pack at 68%, while their lattice packing is about the same.[4-5]

Monte Carlo simulation of packing of hard ellipses.
(image from the ChaikinLab Condensed Matter Physics Laboratory at New York University.)
Their
computer simulations found that a random stacking of
ellipsoids, which are closer in
shape to a sphere than the
lenticular M&Ms, has a larger density than the close-packed lattice packing of spheres. Further work by Torquato and
colleagues showed that the densest packings of
tetrahedra,
icosahedra,
dodecahedra, and
octahedra were 0.823, 0.836, 0.904, and 0.947, respectively.[6-13] This is an interesting result, since the dodecahedra and icosahedra approximate a sphere to a high degree but pack much better.

Because of inflation, the old saying, "a penny for your thoughts," should be updated to offering a quarter, instead.
This pile of US quarter dollar coins illustrates another type of packing, that of disk-shaped objects.
(Photo by the author)
A
disk is another type of simple
geometric object, and the random stacking behavior of disks has been studies by a
researchers from the
East China Normal University (Shanghai, China).[14-15] Their
experiments with small, coin-sized,
plastic disks have revealed the formation of randomly oriented stacks in their packing.[15] Just as the random packing of other shapes has important consequences in the
mechanics of
materials, disk packing applies to the
flow and
optical properties of
technological materials, such as
liquid crystals, and also the mechanical properties of
clays.[15] The
frictional forces acting between
flat flakes in clays stabilize this material against
temperature.[15]
Their experiments used
hollow disks about 30
millimeters in
diameter and 5 millimeters in
thickness.[15] The disks were hollow so they could be filled with a
gel that was strongly visible in
magnetic resonance imaging (MRI) to allow the disk
positions to be
measured.[15] Twelve hundred disks were
poured into a
rectangular container and lightly
shaken by repeated dropping to a hard
surface several times from a
height of one
centimeter; but, to avoid
boundary effects, only about 500 disks at the center were
analyzed.[15]
When first loaded, many of the disks lay flat in a random arrangement, but shaking leads to a
compacted state with some disks forming short stacks that are randomly aligned with each other.[15] As the density increases, the alignment decreases, and this
correlation has been observed in a prior experimental and
theoretical study of packings in clays.[15] The researchers speculate that more intense shaking might lead to a globally aligned
columnar state.[15] As for potential applications, study
coauthor,
Chengjie Xia, states that the porosity of
concrete could be adjusted by addition of disk-like particles.[15]

Ancient Greek clayware, circa 800 BC, at the National Hellenic Museum.
(Wikimedia Commons image by "GreekDude1." Click for larger image.)
References:
- David Pescovitz, "Stash of 100,00 ancient coins found at construction site," BoingBoing, November 15, 2023.
- Thomas C. Hales, "An overview of the Kepler conjecture," arXiv, May 20, 2002, https://doi.org/10.48550/arXiv.math/9811071.
- Thomas C. Hales, "A proof of the Kepler conjecture, Annals of Mathematics, vol. 162, no. 3 (2005), pp. 1065-1185, https://doi.org/10.4007/annals.2005.162.1065.
- Steven Schultz, "Sweet science: Common candies yield physics discovery," Princeton University Press Release, February 12, 2004.
- Aleksandar Donev, Ibrahim Cisse, David Sachs, Evan A. Variano, Frank H. Stillinger, Robert Connelly, Salvatore Torquato and P. M. Chaikin, "Improving the Density of Jammed Disordered Packings Using Ellipsoids," Science, vol. 303, no. 5660 (February 13, 2004), pp. 990-993.
- Aleksandar Donev, Frank H. Stillinger, P. M. Chaikin and Salvatore Torquato, "Superdense Crystal Packings of Ellipsoids," arXiv, March 10, 2004. Also at Physical Review Letters.
- S. Torquato, "Reformulation of the Covering and Quantizer Problems as Ground States of Interacting Particles," arXiv, September 8, 2010. Also at Physical Review E.
- Salvatore Torquato and Frank H. Stillinger, "Jammed Hard-Particle Packings: From Kepler to Bernal and Beyond," arXiv, August 17, 2010. Also at Reviews of Modern Physics.
- S. Torquato and Y. Jiao, "Exact Constructions of a Family of Dense Periodic Packings of Tetrahedra," arXiv, April 30, 2010. Also at Physical Review E.
- Y. Jiao, F. H. Stillinger and S. Torquato, "Novel Features Arising in the Maximally Random Jammed Packings of Superballs," arXiv, January 4, 2010. Also at Physical Review E.
- S. Torquato and Y. Jiao, "Dense Packings of Polyhedra: Platonic and Archimedean Solids," arXiv, September 9, 2009. Also at Physical Review E.
- S. Torquato and Y. Jiao, "Dense Packings of the Platonic and Archimedean Solids," arXiv, August 27, 2009. Also at Nature.
- S. Torquato, T. M. Truskett and P. G. Debenedetti, "Is Random Close Packing of Spheres Well Defined?," arXiv, March 25, 2000. Also at Physical Review Letters.
- Yunhao Ding, Jing Yang, Chenyang Wang, Zhichao Wang, Jianqi Li, Bingwen Hu, and Chengjie Xia, "Structural Transformation between a Nematic Loose Packing and a Randomly Stacked Close Packing of Granular Disks, " Physical Review Letters, vol. 131, no. 9 (September 1, 2023), Article no. 098202, https://doi.org/10.1103/PhysRevLett.131.098202
- Philip Ball, "Packing Disks in a New Way," Physics, vol. 16, no. 150, September 1, 2023.
- How to stack coins? ECNU research team reveals the stack structure transformation mechanism of disk-like particles, East China University Press Release, September 9, 2023.
Linked Keywords: Uncle; United States Marine Corps; World War II; welding; welder; youth; youthful; 1950s; glass bottle; container; choice; soft drink; bounty (reward); recycling; return; city; wandering; roam; neighborhood; Radio Flyer wagon; night; waste management; trash collection; discard">discarded; exchange; cash; roll-your-own cigarette; machine; mechanical device; glass; jar; coin; sort; numismatics; rare coin; face value; hoard; cache; ancient history; ancient; Common Era; BC; Japan; Japanese; construction; mile; Tokyo; stack; jumbled mass; financial cost of cigarette smoking (cartoon); smoking; finance; financial; burden; health; government; smoking cessation; expense; disease; health problem; recoup; cigarette taxes in the United States; George Harrison (1943-2001); The Beatles; throat cancer; lung cancer; Wellcome Trust; Wikimedia Commons; cigarette pack; relative density; efficient stacking; cylinder (geometry); matchbook; match; sphere packing; packing of spherical objects; density; dense; packing of identical spheres; greengrocer; fruit; close-packing of equal spheres; close-packing arrangement; Johannes Kepler (1571-1630); conjecture; Strena Seu de Nive Sexangula; materials scientist; crystallographer; atom; cubic crystal system; face-center-cubic; crystal structure; crystal lattice; metal; aluminum; copper; coordination number; twelve neighboring spheres; three-dimensional space; Kepler conjecture; Carl Friedrich Gauss (1777-1855); mathematical proof; prove; computer-assisted proof; Thomas Hales (b. 1958); randomness; randomly; physicist; Paul Chaikin; chemist; Salvatore Torquato; oblate spheroid; M&M candy; Monte Carlo method; Monte Carlo simulation; hardness; hard; ellipse; ChaikinLab Condensed Matter Physics Laboratory; New York University; computer simulation; ellipsoid; geometry; shape; lenticular; colleague; tetrahedron; tetrahedra; icosahedron; icosahedra; dodecahedron; dodecahedra; octahedron; octahedra; inflation; saying; a penny for your thoughts; US quarter dollar coin; disk (mathematics); geometric; research; researchers; East China Normal University (Shanghai, China); experiment; plastic; classical mechanics; material; fluid dynamics; flow; optics; optical; technology; technological; liquid crystal; clay; friction; frictional; force; flatness (mathematics); flat; flake; temperature; hollow; millimeter; diameter; thickness; gel; magnetic resonance imaging (MRI); position (vector); measurement; measure; pour; cuboid; rectangular; vibration; shake; surface; altitude; height; centimeter; boundary (topology); analysis; analyze; compaction; compacted; correlation; theory; theoretical; cylinder (geometry); columnar; author; coauthor; Chengjie Xia; concrete; Ancient Greek clayware circa 800 BC; National Hellenic Museum.