| Tikalon Blog is now in archive mode.
An easily printed and saved version of this article, and a link
to a directory of all articles, can be found below: |
|
This article |
| Directory of all articles |
Another Piece of Pi
July 28, 2010
Last week we celebrated "
Pi Approximation Day," July 22, or 22/7 when written in a day/month format. This fraction is a close approximation to the value of pi, a fact discovered by
Archimedes. Archimedes estimated the value of pi using polygons inscribed in, and circumscribed around, a circle. It's a simple matter to get the perimeters of the polygons and ratio them to the radius of the circle to get π ≈ P/(2R), where P is the perimeter and R is the radius of the circle. As shown in the figure, it's possible to find the length of one side of any circumscribed polygon by using the tangent function. Archimedes didn't have trig tables, or a calculator with trig functions, so his analysis was limited to particular triangles, but the idea is the same. Archimedes obtained his estimate of 22/7 for pi using a circumscribed 96-sided polygon. This is the value of pi I learned in elementary school, and it's great for homework problems at that age level, when only integer arithmetic is known.
Ptolomey decided to best Archimedes with a 360-sided polygon, from which he obtained 3,141666..., a value that's correct to three decimal places.
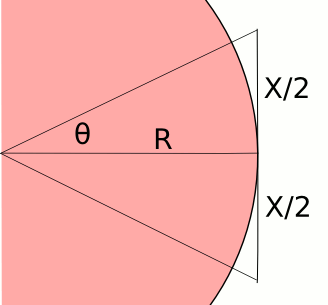
Circumscribed polygon
Computer techniques have now allowed a calculation of pi to 2,699,999,990,000 decimal digits[1]. Our present estimate of the
diameter of the universe is 93 billion light-years (8.8 x 10
26 meters), so we only need twenty-seven digits of pi to calculate the circumference of the universe to better than a meter, and thirty-eight digits to get a value of the circumference closer than the
size of an atom.
In a
previous article (Buffon's Needle, July 19, 2010), I showed a physical method, devised by
Georges-Louis Leclerc, Comte de Buffon, for obtaining a value of pi by dropping needles on floor boards and counting the fraction of needles that crossed the cracks between boards. Today, I'll present a different method to estimate pi that depends also on randomness. I was reminded of this method while reading an article[2] by
David Patterson, a well known computer scientist, in this month's
IEEE Spectrum. Patterson was addressing the question of how useful
multi-core processors really are, and he gave some examples of problems that can be solved by parallel programming methods, including estimation of pi
"You could, for instance, determine the value of pi. Just compute what happens when you throw darts at a square board. If the darts hit random points on the square, what fraction of them fall within the largest circle you can draw on the board? Calculate that number for enough darts and you'll know the area of the circle. Dividing by the radius squared then gives you a value for pi."
I remember this same simulation involving the casting of
millet seed onto a circle inscribed in a square. This was possibly in deference to
Zeno, who had a thing with
millet seeds, but the idea is the same (see figure).
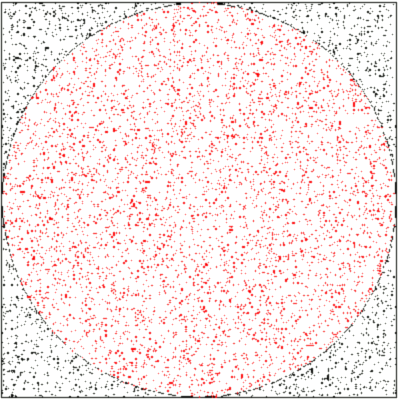
Casting millet seed
This is a
Monte Carlo method[3], and it's quite easy to program. You can review my C code,
here. As you remember, our Buffon's needle calculation made us 95% confident that the value of pi lay between 3.126605 and 3.156433. The millet seeds do a little better. For the same number of trials (10,000), and the same number of actions (100,000), we calculate a mean value of 3.141548 with a standard deviation 0f 0.005213. This means that we're 95% confident that the value of pi lies between 3.131122 and 3.151974, which is somewhat better.
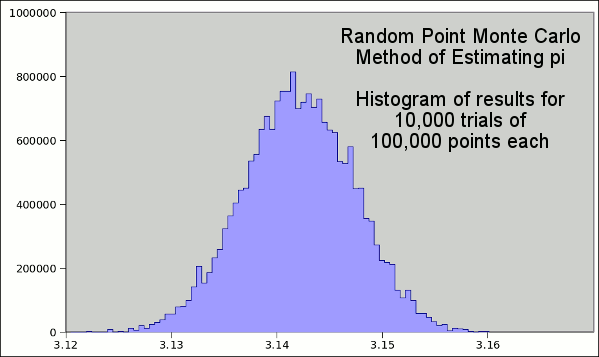
Histogram of pi estimates using the Monte Carlo method
References:
- Digits of pi on Wikipedia.
- David Patterson, "The Trouble With Multicore," IEEE Spectrum (July, 2010)
- For the history of the computational Monte Carlo method, see my previous article, Nicholas Metropolis, June 11, 2010.
Permanent Link to this article