Singing Saw
July 4, 2022
In several previous articles, I've mentioned
kitchen chemistry, the use of common
household materials in doing simple
experiments. There's also
kitchen music, well known to
pot-
banging children and their
parents, in which kitchen items are used to produce music. Aside from
percussive instruments such as
pots and pans, there's also the
glass harp in which
rubbing a
finger around the
rim of a
beverage glass results in a
tone that depends on the type of
glass and the
level of
fluid that it contains. The very
inventive Benjamin Franklin (1706-1790) created an advanced version of this in his 1761
glass harmonica.

A 1492 woodcut by Franchino Gafori depicting a glass harp in Theorica musicae (Milan, 1492).
This image appeared on page 11 of Thomas Bloch's L'harmonica de verre ou glassharmonica: données et synthèse historique, organologique, acoustique et bibliographique sur l'instrument de Benjamin Franklin et sur les instruments dérivés, Bulletin FRBNF35344835 of the Conservatoire National Supérieur de Musique de Paris, 1988-89.
(Portion of a Wikimedia Commons image.)
Just as in rubbing a
bow on a
violin string, rubbing a finger around the rim of a beverage glass will excite a
standing wave in the rubbed
medium.[1] In the case of a violin, the medium is the string, the
standing wave of the string is along its
length, and the
frequency is determined by the
linear density and
tension of the string. For the singing glass, the standing wave is in the body of the glass, extending between the rim and the
water line, and that explains why a change in the water level changes the frequency.[1] The
sound of the violin string is
amplified by the violin body, and the sound of the singing glass is amplified in the
air space inside the glass. You can also imagine affixing a singing glass to something like a violin body to produce a higher
amplitude sound.
Moving from the kitchen to the
cellar workshop leads us to the
musical saw. A musical, or
singing saw, is a
flexible steel hand saw,
bent into an
"S" shape, that's bowed on its flat edge. The musical saw is used in
folk music in the
United States and other
countries, a likely result of the ubiquity of handsaws on
farms. The
popularity of the singing saw increased with easy access to inexpensive, flexible steel in the early
19th century.
A musical saw
performance is something you might see in a
video clip of a
1950s television variety show, such as
The Ed Sullivan Show. The actress,
Marlene Dietrich (1901-1992) was a notable musical saw
artist, a consequence of her violin
training. Today's
youth have likely never heard of a musical saw,
Ed Sullivan, or Marlene Dietrich. On the other hand,
Baby Boomers would confuse
The Weeknd with the
weekend.
The key to the
acoustics of the musical saw is its "S" shape, created by holding the saw
handle between the
knees and bending it into shape with one
hand.
vibration is
damped in the
curved parts of the saw
blade, but the center of the S-curve is relatively flat, creating a
sweet spot for tone production (see figure). Bowing produces standing waves across the blade width; and, as a result, forming this
area in a wider section of blade leads to lower frequency sound. Since a width
difference of 2:1 is needed to produce an
octave's range of frequency, there are saws
designed specifically for music production. Adjusting the S-curve allows control of the position of the flat section and the frequency produced.
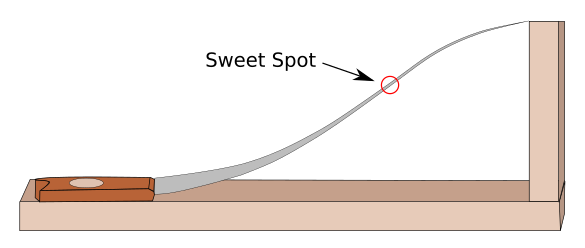
Schematic diagram of a singing saw clamped into an 'S' shape on a test jig. The center of the flat area, called the "sweet spot," is the place at which bowing produces the best sound. The sweet spot is what physicists would call an area of localized vibrational modes, a confined area which resonates without losing energy at the edges. (Created using Inkscape. Click for larger image.)
There have been
scientific studies of the acoustics of the singing saw,[1-3] the most recent of which, by
scientists at
Harvard University (Boston, Massachusetts), has appeared as an open access article in the
Proceedings of the National Academy of Sciences.[3] Musical instruments, such as the aforementioned glass harp, need to produce sustained
notes.[3] This quality is a part of the
design of
musical instruments from
tubas to
tablas, but a saw is not designed to incorporate an
acoustic resonator as would a musical instrument.[3-4]
The resonant area for a singing saw is localized at the
inflection point between the two
bends of its "S" shape.[3] Says
Petur Bryde, a
co-first author of the
paper describing this study,
"How the singing saw sings is based on a surprising effect... When you strike a flat elastic sheet, such as a sheet of metal, the entire structure vibrates. The energy is quickly lost through the boundary where it is held, resulting in a dull sound that dissipates quickly. The same result is observed if you curve it into a J-shape. But, if you bend the sheet into an S-shape, you can make it vibrate in a very small area, which produces a clear, long-lasting tone."[4]
In their
experiments, the
research team clamped a saw in two configurations - a "J" shape and an "S" shape. The "S" shape has an inflection point (the sweet spot), while the "J" shape doesn't.[4] It was found that only the "S" shape will
sing, and the details of its shape are unimportant.[4] The "S" could have a big curve at the top and a small curve at the bottom, or visa versa.[4] The existence of the inflection point is all that matters.[4]
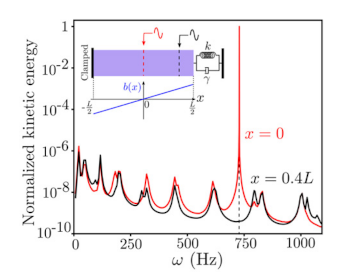
Sweet spot resonance for a singing saw.
These are resonance curves for a shell with curvature as shown, periodically driven at the inflection point (x = 0, the red line) and away from it (x = 0.4, the black line) for varying frequency, with ω = 740 Hz being the first localized mode.[3]
(Fig. 3a of ref. 3, licensed under the Creative Commons Attribution-NonCommercial-NoDerivatives License 4.0.[3])
Variation in the saw blade curvature along its length controls the localization of trapped acoustic states, and this makes a singing saw the
high-quality geometrically tunable
oscillator that it is.[3] This has an
analogy to the edge states in
topological insulators.[3] Topological insulators are
electrical insulators that have the surprising property that they will
conduct electricity in their
surface or edges, but nowhere in their
bulk.[4] The opposite curves in a saw produce what are in effect internal
edges.[4] The
physics behind the singing saw may allow the design of high quality resonators for
sensors,
nanoelectronics, and
photonics.[4] The team plans to expand their research by investigating doubly curved structures, such as
bells.[4] This research was
funded by the
National Science Foundation.[4]
While on the topic of physics as applied to music, I'll mention an interesting study presented at a recent
conference and available on
arXiv.[6] The study is about
rickrolling in the
academic literature.[6] Rickrolling is giving a
link to an expected topic that's actually a link to the
YouTube video of Rick Astley's, "Never Gonna Give You Up."[7] Possibly because of this, the video has more than 1.2 billion views.[7] I was confused the first time I was rickrolled more than a
decade ago, but I've come to enjoy both the
song and the video. The
comment in the arXiv
abstract for the study is a rickroll. As of March, 2022, there are 23 academic documents intentionally rickrolling the reader. This is not a huge number, but another indication that scientists and academics are
playful people.[7]
References:
- Reuben Leatherman, Justin C. Dunlap, and Ralf Widenhorn, "The Fourier Spectrum of a Singing Wine Glass," American Journal of Physics, vol. 87, no. 10 (September 18, 2019), pp. 829-835, doi: 10.1119/1.5124230. A PDF file of this paper appears here.
- Randy Worland, "Vibroacoustics of the Musical Saw: Experimental Measurements of Trapped Mode Shapes and Frequencies vs. Blade Curvature," The International Institute of Acoustics and Vibration, ICSV26 (Montreal, Canada, July 7-11, 2019), PDF File.
- Suraj Shankara, Petur Brydeb, and L. Mahadevana, "Geometric control of topological dynamics in a singing saw," Proc. Natl. Acad. Sci, vol. 119, no. 17 (April 21, 2022), Article no.e2117241119, https://doi.org/10.1073/pnas.2117241119. This is an open access publication with a PDF file here.
- Leah Burrows, "The physics of a singing saw," Harvard University School of Engineering and Applied Sciences Press Release, April 21, 2022.
- Austin Blackburn plays 'Ave Maria' on musical saw, YouTube Video by msawman, June 10, 2008.
- Benoit Baudry and Martin Monperrus, "Exhaustive Survey of Rickrolling in Academic Literature," arXiv, April 14, 2022. Part of the 2022 SIGBOVIK conference. SIGBOVIK is an annual multidisciplinary conference specializing in lesser-known areas of academic research. The 2022 conference proceedings can be found as a PDF file here.
- Rick Astley, "Never Gonna Give You Up (Official Music Video), YouTube, October 25, 2009.
Linked Keywords: Amateur chemistry; kitchen chemistry; household; material; experiment; kitchen; music; cookware and bakeware; pot; percussion instrument; banging; child; children; parent; pots and pans; glass harp; rub; rubbing; finger; rim; drinkware; beverage glass; musical note; tone; glass; height; level; fluid; invention; inventive; Benjamin Franklin (1706-1790); glass harmonica; woodcut; Conservatoire de Paris; Conservatoire National Supérieur de Musique de Paris; Wikimedia Commons; bow (music); violin; string (music); standing wave; medium; string vibration; standing wave of a string; length; frequency; linear density; tension (physics); water; sound; amplitude; amplify; volume; air space; basement; cellar; workshop; musical saw; stiffness; flexible; steel; hand saw; bending; bent; sigmoid function; "S" shape; folk music; United States; country; farm; popularity; 19th century; performance; video clip; 1950s; television program; variety show; The Ed Sullivan Show; Marlene Dietrich (1901-1992); artist; training; youth; Ed Sullivan; Baby Boomer; The Weeknd; weekend; acoustics; handle; knee; hand; vibration; damping; damped; curve; curved parts; blade; area; ratio; difference; octave; design; Schematic of a singing saw; schematic diagram; musical saw; singing saw; clamp (tool); clamped; jig (tool); test jig; sound; physicist; vibration; vibrational; normal mode; mode; resonance; resonate; energy; edge (geometry); Inkscape; science; scientific; scientist; Harvard University (Boston, Massachusetts); Proceedings of the National Academy of Sciences; note; musical instrument; tuba; tabla; acoustic resonance; acoustic resonator; inflection point; Petur Bryde; author; scientific literature; paper; surprise (emotion); surprising; impulse (physics); strike; elasticity (physics); elastic; plane (geometry); sheet; metal; boundary (topology); dissipation; dissipate; shell (structure); curvature; periodic function; periodically; hertz; Hz; Creative Commons Attribution-NonCommercial-NoDerivatives License 4.0; Q factor; high-quality; geometry; geometrical; harmonic oscillator; analogy; topological insulator; electrical insulator; electrical conductor; surface; bulk; physics; sensor; nanoelectronics; photonics; bell; funding of science; funded; National Science Foundation; academic conference; arXiv; rickrolling; academic publishing; academic literature; hyperlink; link; YouTube video; decade; song; note (typography); comment; abstract (summary); play (activity); playful.