| Tikalon Blog is now in archive mode.
An easily printed and saved version of this article, and a link
to a directory of all articles, can be found below: |
|
This article |
| Directory of all articles |
Chaotic Cavities
May 15, 2013
Resonators can store
energy. An obvious
mechanical example is a
pendulum. As an
electrical example, we have the
quartz crystal, which will be set into resonance if we ping it with a
voltage pulse. The crystal's resonance decays according to the well-known
function
A(t) = Ao e-λt cos(t)
where
A(t) is the amplitude as a function of time,
Ao is the initial amplitude, and lambda (
λ), called the
log decrement, sets the rate of decay. I wrote about such
damped harmonic oscillators in a
previous article (Graphene Resonators, June 24, 2011). In a quartz crystal oscillator, the degree of decay, or
damping, is related to the crystal's
Q-factor; viz., Q = 2π(Energy Stored/Energy Lost per cycle).
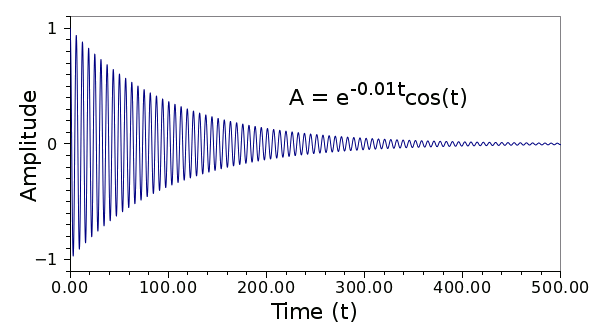
Amplitude of a damped harmonic oscillator. In this case, the log decrement is 0.01, giving the equation shown on the plot. (Graph rendered with Gnumeric.)
Harmonic oscillators are extremely useful, and there must be dozens of
electronic oscillators in your house right now, clocking
microprocessors in things such as
cellphones and
television remotes. There's another type of oscillator that's not as useful, but much more interesting. This is the
chaotic oscillator, the most common example of which is
Chua's circuit,[1-2] named after its inventor,
Leon Chua, a
professor of
Electrical Engineering.
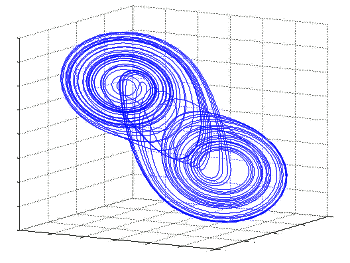
One representation of the chaos implicit in the Chua oscillator.
This graph of its double scroll attractor is produced by plotting three different voltages in a simulation of the circuit.
(Via Wikimedia Commons.)[3)]
Chaotic oscillators would have been just a curiosity of
physics without an application were it not for a discovery made by
scientists at the
US Naval Research Laboratory in 1990, one of whom was a classmate of mine in
graduate school. They discovered that it's possible to
synchronize chaotic oscillators remotely.[4] Their report on this research was named a
Physical Review Letters Milestone for 1990.
How useful are two coupled chaotic oscillators? The voltage output of a chaotic oscillator is very dependent on the values of its components and its initial state. Small changes in any of these for a chaotic oscillator lead to large changes in the time series of its voltage values.
This means that you can conveniently generate the same
sequence of random numbers simultaneously at two different places, and even you won't know what number follows another in the sequence. Such a
physical random number generator can be used to send
coded messages using the unbreakable
cryptographic technique known as the
one-time pad. Aside from this application, chaos has been mostly descriptive and rarely proscriptive.[5]
An international team of scientists and
engineers from the
King Abdullah University of Science and Technology (
Saudi Arabia), the
University of St Andrews (
UK),
University of Bologna (
Italy) and the
University of York (UK) have found another practical use for chaos. They've demonstrated that imposition of chaos causes a six-fold increase of the stored
energy in a resonant
optical cavity as compared to its
classical counterpart of the same
volume.[6-7]
This discovery goes against the idea that chaos always diminishes the performance of devices.[7] The
research involved
ab initio simulations and
experiments on
photonic-crystal resonators which store light energy by bouncing it between
mirrors. In the chaotic case, the mirrors were deformed to disrupt the normal path of the
light rays. The demonstrated principle is that increasing the number of
degrees of freedom of a system allows more energy storage in the
equipartition of energy among the states.[6-7]
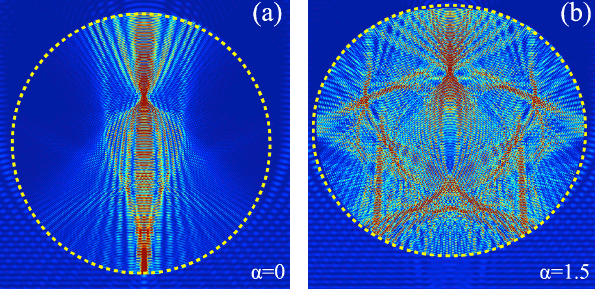
Patterns of light distribution in a normal cavity resonator (left) and a chaotic cavity resonator (right). The extra resonant modes for the chaotic cavity are apparent.(York University image, Fratalocchi et al./Nature Photonics, used with permission.)[7)]
Even simple cavities, such as
glass microspheres and
polystyrene microspheres, showed more stored energy when they were deformed.[6-7] Says Thomas F. Krauss, a professor of physics at York University and a coauthor of the study,
"Besides the obvious implications at the fundamental level, where we demonstrate the existence of a fundamental principle of thermodynamics in the framework of Photonics, our results also have real-world practical implications."[7]
One practical application would be to increase the interaction time of
solar radiation in
photovoltaic cells to increase the
energy conversion efficiency. York university is already pursuing a program relating to commercial devices.[7-8]
References:
- Bertie Genade, "The Chua chaotic oscillator".
- A Tamaševicius, G Mykolaitis, V Pyragas and K Pyragas, "A simple chaotic oscillator for educational purposes," European Journal Of Physics, vol. 26 (November 3, 2004), pp. 61-63.
- Chua Circuits Web Site by V. Siderskiy.
- Louis M. Pecora and Thomas L. Carroll, "Synchronization in chaotic systems," Phys. Rev. Lett., vol. 64, no. 8 (February 19, 1990) pp. 821-824. A PDF copy is available here.
- Jaroslav Stark and Kate Hardy, "Chaos: Useful at Last?" Science, vol. 301, no. 5637 (August 29, 2003) pp. 1192-1193.
- C. Liu, A. Di Falco, D. Molinari, Y. Khan, B. S. Ooi, T. F. Krauss and A. Fratalocchi, "Enhanced energy storage in chaotic optical resonators," Nature Photonics, Advance Online Publication, May 5, 2013, doi:10.1038/nphoton.2013.108.
- Chaos proves superior to order, University of York Press Release, May 7, 2013.
- PrimaLight Research Web Site.
Permanent Link to this article
Linked Keywords: Resonator; energy; mechanics; mechanical; pendulum; electronics; electrical; quartz crystal; voltage; pulse; function; log decrement; damped harmonic oscillator; damping; Q-factor; amplitude; equation; Gnumeric; electronic oscillator; microprocessor; cellphone; television remote; chaos theory; chaotic; Chua's circuit; Leon Chua; professor; Electrical Engineering; Chua oscillator; double scroll attractor; simulation; Wikimedia Commons; physics; scientist; United States Naval Research Laboratory; graduate school; synchronization of chaos; synchronize chaotic oscillators; Physical Review Letters Milestone; random sequence; sequence of random numbers; physical random number generator; code; cryptography; cryptographic; one-time pad; engineer; King Abdullah University of Science and Technology; Saudi Arabia; University of St Andrews; United Kingdom; UK; University of Bologna; Italy; University of York; energy; optical cavity; classical physics; volume; research; first principles; ab initio; experiment; photonic-crystal; mirror; light ray; degrees of freedom; equipartition theorem; equipartition of energy; glass; microsphere; polystyrene; sunlight; solar radiation; solar cell; photovoltaic cell; energy conversion efficiency; Louis M. Pecora and Thomas L. Carroll, "Synchronization in chaotic systems," Phys. Rev. Lett., vol. 64, no. 8 (February 19, 1990) pp. 821-824.