Graphene Mass Standard
February 16, 2012
Mass is of fundamental importance in
physics. Our system of units, now called the
International System of Units (SI, for Système international d'unités), was called the MKS system, for
meter,
kilogram,
second. The primary mission of
CERN's very expensive
Large Hadron Collider (LHC) is the search for the
Higgs boson, the particle that's conjectured to give all other
elementary particles their mass.
For all the importance of mass, the method for standardizing mass is a relic of a
classical physics period long passed. The present mass standard is a physical object, a cylinder of a 90%
platinum - 10%
iridium (by weight)
alloy, the
international prototype kilogram. This object, maintained at the
Bureau International des Poids et Mesures (International Bureau of Weights and Measures), is lovingly compared with copies that are distributed to international weights and measures organizations for comparison against their own physical mass standards.
As you can imagine, all the care in the world, and even the use of such a
durable and
non-tarnishing alloy, can't eliminate all
errors. In fact, the
catalytic action of platinum might be responsible for reactions with
polluted air that add a little more mass to this object, year after year. However, the change has been small, less than 100
parts per billion (ppb), as can be seen in the graph that shows the upwards increase in mass of eleven transfer mass standards.
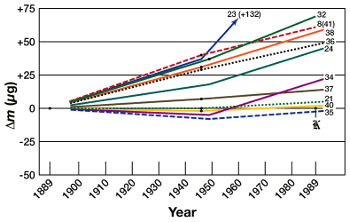
Upwards drift of eleven international mass standards.
(Via Wikimedia Commons).
There have been recent efforts to replace the international prototype kilogram with a mass standard that is linked to fundamental
physical constants. Aside from a possible advantage in this approach of improved future accuracy, such a standard would not be linked to a specific object in a specific location. Every national standards body could have its own very precise mass reference. I outlined two approaches to a mass standard in previous articles (
Mass Standard, November 1, 2010 and
Standard Kilogram, June 28, 2007.
The
Avogadro project is an international collaboration to replace the international prototype kilogram with an equivalent object made from
isotopically pure silicon-28 (
28Si). Natural
silicon is composed of the isotopes,
28Si, 92.23%,
29Si, 4.67%, and
30Si, 3.1%, so the
isotope separation is an important step. After that, perfect
crystals of
28Si are made and formed into perfect
spheres. These spheres would contain an
Avogadro number of atoms, as determined by the
volume. These spheres would have a reproducible weight of
very nearly 28 grams, and they could be made in multiply exact copies at any place at any time.
A more fundamental technique is the
watt balance, which would link the kilogram to
Planck's constant. The equipment required to realize such a measurement is quite complicated, but it is a more accessible measurement, since silicon isotope separation is not required. The technique is called a watt balance, since the weight of a test mass is balanced against the product of an
electric current and a
voltage, the units of which are related only to Planck's constant and the
speed of light. The
US National Institute of Standards and Technology (NIST) has achieved an error for this measurement of 36 ppb. It's agreed that when the errors are at the 10 ppb level, this will be a viable standard.
Then there's
graphene, our present wonder material.
Phil Fraundorf of the
Department of Physics and Astronomy and the
Center for NanoScience, the University of Missouri (St. Louis, MO), has just posted a paper on
arXiv in which he proposes a crystal of
carbon (
12C) formed from graphene sheets as a mass standard that contains a
mole of carbon
atoms. Fraundorf writes that
"Graphite is constructed from graphene sheets whose controlled synthesis at the atomic-scale is likely to see great progress by nanotechnologists in the years ahead. If any macroscopic object will be possible to assemble from a chosen number of atoms in the decades ahead, this may be it."
Fraundorf examines the growth of graphite from a
seed plane of twenty four carbon atoms, as shown in the figure. Lateral growth is accomplished by adding units to the periphery, and it can be seen that at every hexagonal edge of the ensemble there are two added atoms m for every added cell element n.
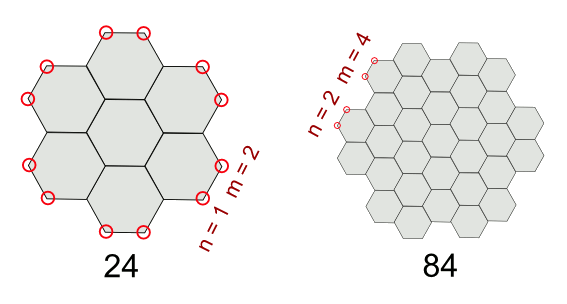
Counting atoms in graphene sheets. (Illustration by author, rendered with Inkscape).
When building an
hexagonal prism of graphene sheets of m layers, the number of atoms N is given by the equation,
N = 3 m2 + (9/2) m3
It's possible to build a structure that comes extremely close to having an
Avogadro's number of atoms, as shown in the table.
| n | m | N |
| 0 | 0 | 0 |
| 1 | 2 | 48 |
| 2 | 4 | 336 |
| 3 | 6 | 1080 |
| 4 | 8 | 2496 |
| 5 | 10 | 4800 |
| 6 | 12 | 8208 |
| 7 | 14 | 12936 |
| 8 | 16 | 19200 |
| 9 | 18 | 27216 |
| 10 | 20 | 37200 |
| 25,575,030 | 51,150,060 | 6.02214 x 1023 |
Such a graphite crystal would be about 1.71
cm high. A
circumscribed cylinder around this crystal would have a diameter of about 1.45 cm. Of course, it would weigh twelve
grams.
Reference:
- P. Fraundorf, "A multiple of 12 for Avogadro," arXiv Preprint Server, January 25, 2012.
Permanent Link to this article
Linked Keywords: Mass; physics; International System of Units; meter; kilogram; second; CERN; Large Hadron Collider; Higgs boson; elementary particle; classical physics; platinum; iridium; alloy; international prototype kilogram; Bureau International des Poids et Mesures; durable; non-tarnishing; errors and residuals in statistics; catalysis; pollution; polluted air; parts per billion; Wikimedia Commons; physical constant; Avogadro project; isotopically pure; silicon-28; silicon; isotope separation; crystal; sphere; Avogadro number; volume; nuclear binding energy; mass defect; watt balance; Planck's constant; electric current; voltage; speed of light; US National Institute of Standards and Technology; graphene; Phil Fraundorf; Department of Physics and Astronomy; Center for NanoScience; arXiv; carbon; mole; atom; seed plane; Inkscape; hexagonal prism; Avogadro's number; centimeter; cm; circumscribe; cylinder; gram.