| Tikalon Blog is now in archive mode.
An easily printed and saved version of this article, and a link
to a directory of all articles, can be found below: |
|
This article |
| Directory of all articles |
Mass Standard
November 1, 2010
Standards are an important part of science, technology and commerce. The
fundamental standards for mass (m), length (l) and time (t) affect our lives every day. Your electronic equipment operates properly because of a frequency standard (frequency = 1/t). Filling your fuel tank? That's a length standard (volume ∼ l
3). Then there's the 48 ounce box of corn flakes (m).
Time can be measured very precisely, since a
second is defined as "the duration of 9,192,631,770 periods of the radiation corresponding to the transition between the two
hyperfine levels of the ground state of the
caesium 133 atom." Having a time standard then allows an easy
definition of length based on the
speed of light. Because of these standards, length and time can be measured with high accuracy.
In contrast, we can measure mass only by comparison with a physical object, the
standard kilogram, maintained at the
Bureau International des Poids et Mesures (International Bureau of Weights and Measures) outside
Paris. This mass standard, known as the "kilogram prototype," is a cylinder of
platinum-
iridium alloy. This is used as a reference mass that allows transfer of a mass standard to other locations where further derivative transfers to other standards laboratories are done. Mass isn't important just for weight. Mass is part of the definitions of the
Ampere,
mole and
candela. The candela is defined as a
power, so its mass dependence is indirect through either the Ampere or force.
Unfortunately, this primary mass standard may have lost or gained nearly 100 micrograms over the century of its existence, which converts to a 100 parts per billion error. This may sound like a small error (10
-7), but the length and time standards are known to at least one part in 10
-10. In short, our standard for mass is a thousand times worse than our other standards. In an interesting example of
self-reference, although the standard kilogram may have changed weight, it
still weighs a kilogram, since it
is a kilogram. For this reason, metrologists have been searching for a replacement for the mass standard, and there are two current approaches to the problem.
One approach attempts to define mass in terms of fundamental constants of nature, much like the length standard is derived from the speed of light and the hyperfine transition in
133Cs. Such an approach is championed by the
US National Bureau of Standards and Technology (NIST) in an apparatus called the
Watt balance. A Watt balance essentially equalizes the force exerted on a mass due to
gravitational acceleration g with a force created by the flow of current
I in a wire (usually wound as a coil) in a
magnetic field. The Watt balance eliminates the need to know the precise geometry of the coil and the magnitude of the magnetic field, since it calibrates itself using
Faraday's law of induction by moving the coil through the field at a known velocity
v and measuring the induced voltage
E.[1] In the end, mass is given by a simple equation,
m = (E I)/(g v)
One important feature of this definition of mass is that electrical current and voltage are defined by fundamental constants, such as
Planck's constant and the speed of light.[2] The Watt balance will transition the definition of mass to a fundamental level. Of course, the devil is in the details, such as magnetic field homogeneity, and that's why the NIST Watt balance looks like the photograph below. Aside from NIST, the Watt balance approach is being pursued at national standards laboratories in
England,
Switzerland and
France; but NIST holds the precision record with a relative uncertainty of 3.6 x 10
-8.[3]

NIST Watt Balance (Steiner/NIST)
The other approach to a mass standard is similar to the present platinum-iridium cylinder. It's a technological
tour de force, but in my mind it's less satisfying than relating mass to the fundamental constants. What it involves is counting atoms in a kilogram-sized object composed of a single atom type. This goal is not as outlandish as it sounds. The growth of perfect crystals of
silicon for
integrated circuits is an extremely well developed industrial process. Huge silicon crystals of extreme perfection can be made, and the atoms in these crystals are arranged in a very regular lattice structure known as
diamond cubic; so, in principle, the number of atoms in a geometrical object can be can be "counted," and the object can be used as a mass standard.[4-8]
One difficulty with this approach is that the silicon must be extremely pure. Exclusion of elements other than silicon is easily done by a method called
zone-refining, but there's another problem. Silicon exists as more than one stable isotope, and the natural abundance of these isotopes is approximately (
28Si, 92.23%), (
29Si, 4.67%) and (
30Si, 3.1%). If crystals of
28Si containing an
Avogadro number of atoms were prepared, they would have a reproducible weight of
almost exactly 28 grams.
This is the approach pursued by an international collaboration called the
Avogadro Project. Isotopically-pure silicon-28 was obtained by
gas centrifuge of SiF
4 gas at the Central Design Bureau of Machine Building,
St. Petersburg, Russia. The isotopically-pure gas was made into elemental silicon at the Institute of Chemistry of High-Purity Substances of the
Russian Academy of Sciences,
Nizhny Novgorod, Russia. A five kilogram
single crystal boule of
28Si was grown at the
Institute for Crystal Growth (Leibniz-Institut für Kristallzüchtung) in
Berlin in 2007.
The crystal was 99.994% pure silicon-28 and
dislocation-free. Impurities are always present in materials, so the impurities were measured using
infrared spectroscopy and
positron lifetime spectroscopy to reveal the following concentrations (units of 10
15 cm
-3):
Carbon, 0.99;
Oxygen, 0.36;
Boron, 0.005;
vacancies, 0.33. An Australian team fabricated two 93.6 mm diameter, one kilogram spheres, referenced to the Australian copy of the standard kilogram, from this crystal. The spheres were machined to incredible smoothness, as shown in the figure.[8]
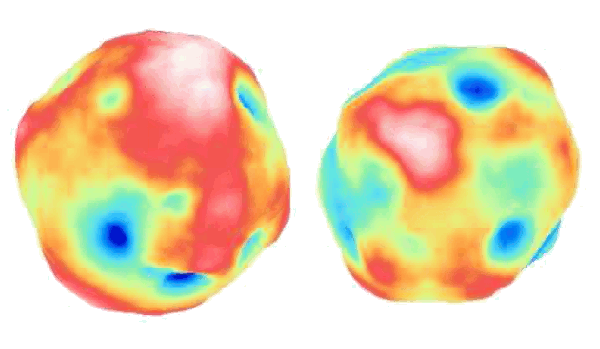
No, these are not the moons of Mars. These are diameter topographs of silicon spheres. The scale is from -63 nm (blue) to 37 nm (red). Peak-to-valley distances are less than 100 nm in each case. (Fig. 3 from Ref. [4], via arXiv).[4]
After an analysis of the actual isotopic concentration of silicon, and laser
interferometry by research groups in
Belgium,
Italy and
Japan to obtain the precise volume of the spheres, the team obtained the following value for Avogadro's constant [4]
6.02214084(18) x 1023 mol-1
The relative uncertainty of of this value is 3.0 x 10
-8. Richard Davis, who heads the mass department of the
International Bureau of Weights and Measures, is quoted in Nature as saying that the relative uncertainty must fall below 2.0 x 10
-8 before these silicon spheres could supplant the current standard.[5] The figure below shows how the silicon spheres compare with other measurements.
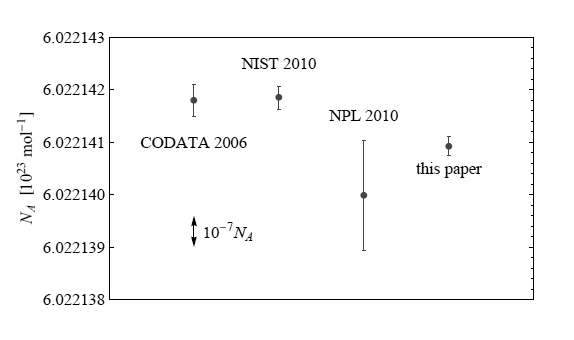
Comparison of Avogadro Number metrology. (Fig. 5 from Ref. [4], "this paper" on graph," via arXiv).[4]
References:
- We used a similar approach at one laboratory at which I worked to measure magnets by moving them at a known speed through a coil. This sounds easy to do, but the measurements were done at only four degrees above absolute zero.
- Ben Stein, "'Sí' on the New SI: NIST Backs Proposal for a Revamped System of Measurement Units," NIST Press Release, October 26, 2010.
- R.L. Steiner, E.R. Williams, R. Liu and D.B. Newell, "Uncertainty Improvements of the NIST Electronic Kilogram," IEEE Transactions on Instrumentation and Measurement, vol. 56, no. 2 (April 2007), pp. 592-596.
- B. Andreas, Y. Azuma, G. Bartl, P. Becker, H. Bettin, M. Borys, I. Busch, M. Gray, P. Fuchs, K. Fujii, H. Fujimoto, E. Kessler, M. Krumrey, U. Kuetgens, N. Kuramoto, G. Mana, P. Manson, E. Massa, S. Mizushima, A. Nicolaus, A. Picard, A. Pramann, O. Rienitz, D. Schiel, S. Valkiers and A. Waseda, "An accurate determination of the Avogadro constant by counting the atoms in a 28Si crystal," arXiv Preprint (October 12, 2010).
- Geoff Brumfiel, "Elemental shift for kilo," Nature, vol. 467 (October 19, 2010), p. 892.
- Ronald F. Fox and Theodore P. Hill, "An Exact Value for Avogadro's Number," American Scientist, vol. 95, no. 2 (March-April 2007).
- Nicola Jones, "Silicon crystal cooked to perfection," Nature Online (29 May 2007).
- Devin Powell, "Roundest objects in the world created" (New Scientist Online, July 1, 2008).
- Standard Kilogram, This Blog, June 28, 2007.
- The Quantity of Matter, This Blog, July 24, 2008.
- Kilogram page on Wikipedia.
Permanent Link to this article
Linked Keywords: International System of Units; SI; time; hyperfine levels; caesium 133; meter; speed of light; Kilogram Prototype; standard kilogram; Bureau International des Poids et Mesures; Paris; platinum; iridium; Ampere; mole; candela; power; self-reference; US National Bureau of Standards and Technology; NIST; Watt balance; gravitational acceleration; magnetic field; Faraday's law of induction; Planck constant; England; Switzerland; France; NIST Watt Balance; tour de force; silicon; integrated circuits; diamond cubic; zone-refining; Avogadro number; nuclear binding energy; mass defect; Avogadro Project; gas centrifuge; St. Petersburg, Russia; Russian Academy of Sciences; Nizhny Novgorod, Russia; single crystal boule; Institute for Crystal Growth; Berlin; dislocation; infrared spectroscopy; positron lifetime spectroscopy; Carbon; Oxygen; Boron; vacancies; interferometry; Belgium; Italy; Japan; International Bureau of Weights and Measures.