Experimental Mathematics
November 2, 2011
Mathematics has a tradition that's based on the importance of
proof. If mathematicians had formal
battle colors, they would be emblazoned with the letters, QED. QED is the abbreviation for the Latin,
Quod Erat Demonstrandum,
that which was to be demonstrated, a phrase that was traditionally placed at the end of mathematical proofs.

Mathematics Battle Flag.
Based on the Bedford Battle Flag, used in the Battle of Concord (April 19, 1775), and thought to be the first flag of the American Revolution.
(Via Wikimedia Commons))
The ubiquity of
electronic computers has begun to change this philosophy, somewhat, but with push-back from the traditionalists. The problem, of course, is the
fallibility of computer code. Although there have been efforts to
prove the correctness of computer codes, this is difficult to do in practice, so most computer programs are presumed to function correctly because they seem to give the right answers. I'm certain this is how most
scientists verify the operation their own programs. They feed them known datasets and are comfortable when they get the "right" answers.
The first "proof" of the
Four Color Conjecture was done by computer. The conjecture, that four colors will suffice to color any planar map such that adjoining colored regions never have the same color, was shown to be correct by
Kenneth Appel and
Wolfgang Haken in 1976. Appel and Haken used a computer to analyze every conceivable map and demonstrated that the conjecture was true. Since some people were still not convinced, Appel and Haken published a more detailed description of their methods in 1986.[1]
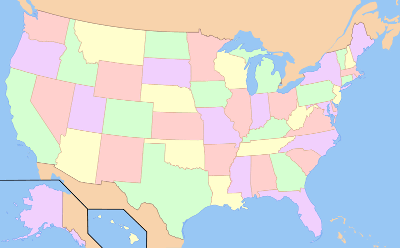
One example of a four color map. Note the famous Four Corners point at the boundaries of Arizona, Colorado, New Mexico and Utah.
Graph by Dbenbenn via (Via Wikimedia Commons))
Appel and Haken's method can only be realized with a computer, since the computational workload is too much for mere humans, but simpler problems were solved this way without a computer. As I wrote in a
previous article (A Place for Mathematics, December 17, 2010), this was the technique used by none other than
Euler to show that the
Königsberg Bridge Problem had no solution. Wrote Euler,
"The particular problem of the seven bridges of Königsberg could be solved by carefully tabulating all possible paths, thereby ascertaining by inspection which of them, if any, met the requirement. This method of solution, however, is too tedious and too difficult because of the large number of possible combinations, and in other problems where many more bridges are involved it could not be used at all."[2].
The computer-assisted proof of the Four Color Conjecture was a romp in the park compared with the proof of the
Kepler Conjecture that I mentioned in a
earlier article (Packing, November 30, 2010).
Johannes Kepler was the first to conjecture that a
face-centered-cubic lattice was the
optimal packing of
spheres. This is merely the arrangement of spherical fruit that
greengrocers have used for centuries.
The Kepler Conjecture was
proved by
Thomas Hales and his student,
Sam Ferguson, in 1998. The proof was not published in full until 2006, since it was difficult to confirm its validity.
Hales is working on a project, called
Flyspeck to produce a
formal proof of the Kepler Conjecture. A formal proof is different from a traditional mathematical proof, since all the intermediate logical steps are included from start to finish. In that case, logical errors are far less likely, although the proof is lengthy and harder to follow.
What I consider a significant landmark in the application of computers to mathematics is the
Bailey–Borwein–Plouffe formula, created by
Simon Plouffe, and published by Plouffe,
David H. Bailey and
Peter Borwein. This formula gives you the n-th digit of
pi without the necessity of computing the previous (n-1) digits. You can retrieve the source code of a C program that calculates hex digits of pi using this formula,
here.
There's an interesting
anecdote about the computation of pi.
Roger Penrose, in his 1989 book "
The Emperor's New Mind," conjectured that we might never know whether pi contains ten sequential sevens in its digital expansion. This was reasonable at the time, since statistically (assuming that the digits of pi are random - Still no proof of that!) you would need to examine about 10
10 digits of pi; that is, ten billion. Yasumasa Kanada found that this sequence occurs starting at the 22,869,046,249th digit.[3] We shouldn't be surprised, since 2.7 trillion digits of pi are known at the writing of this article.[4]
Just like scientists, mathematicians get their inspiration from various sources, but mostly prior work. Now that we have fast computers, computers can indicate areas of mathematics that are worthy of study. That's the point of an article by pi formula collaborators, David H. Bailey and Jonathan M. Borwein, in the current issue of the
Notices of the American Mathematical Society.[3,5] Says Bailey,
"By computing mathematical expressions to very high precision, the computer can discover completely unexpected relationships and formulas."[3]
In particular, by expressing the results of calculations using
data visualization techniques, computers can assist mathematicians in what they do in practice, finding
patterns. Computation is a great tool to falsify conjectures, eliminating work by finding counterexamples.[3]
As an example, Bailey and Borwein offer some explorations of
Giuga's Conjecture, a conjecture dating from 1950 that seems to be inaccessible to proof by conventional mathematical methods. Although not proving the conjecture, they were able to find strong evidence that it's true, perhaps inspiring a renewed effort for a proof.[3]
Such computer explorations of fundamental mathematics are part of a new field called "
experimental mathematics." There's a journal,
Experimental Mathematics, published quarterly by
Taylor & Francis.
Many years ago, I published an article in a general interest magazine in which I asked the following question:
Does Mathematical Truth really exist, or will most of mathematics become a tentative consensus of Mathematical Reality mediated by computers?[6]
The proponents of experimental mathematics don't go that far in their philosophy, but it makes you wonder about the mathematical landscape fifty years hence.
References:
- Kenneth Appel and Wolfgang Haken, "Every Planar Map is Four-Colorable," (American Mathematical Society, Providence, RI), 1989.
- L. Euler, "Solutio problematis ad geometrian situs pertinentis," Comm. Acad. Sci. Imper. Petropol.," vol. 8, pp. 128-140, 1736 (as cited in Ole Peters, "The time resolution of the St. Petersburg paradox," arXiv Preprint, November 19, 2010).
- Mike Breen and Annette Emerson, "Experimental Mathematics," American Mathematical Society Press Release, October 13, 2011.
- The Joy of Pi - Pi Facts.
- David H. Bailey and Jonathan M. Borwein, "Exploratory Experimentation and Computation," Notices of the American Mathematical Society, vol. 58, no. 10 (November, 2011), pp. 1410-1419.
- D.M. Gualtieri, "Proof and Truth in Mathematics," Phi Kappa Phi Forum, vol. 83, no. 4 ((Fall 2003)), pp. 6-7. A PDF copy can be found here.
Permanent Link to this article
Linked Keywords: Mathematics; proof; battle colors; Q.E.D.; Quod Erat Demonstrandum; Wikimedia Commons; electronic computer; Verification and Validation; fallibility of computer code; formal verification; correctness of computer code; scientist; Four Color Conjecture; Kenneth Appel; Wolfgang Haken; Four Corners; Arizona; Colorado; New Mexico; Utah; Euler; Königsberg Bridge Problem; Kepler Conjecture; Johannes Kepler; face-centered-cubic lattice; optimal packing; sphere; greengrocer; Thomas Hales; Sam Ferguson; Flyspeck; formal proof; Bailey–Borwein–Plouffe formula; Simon Plouffe; David H. Bailey; Peter Borwein; pi; anecdote; Roger Penrose; The Emperor's New Mind; Notices of the American Mathematical Society; data visualization; pattern; Agoh–Giuga conjecture; Giuga's Conjecture; experimental mathematics; Experimental Mathematics; Taylor & Francis.