A Place for Mathematics
December 17, 2010
Nearly every important
mathematical theorem or law of
physics is named for its originator. This tradition goes back at least as far as
Pythagoras and the
Pythagorean theorem at a time about 500 B.C. There are, however, some mathematics that bears a place name. The most famous is probably the
Königsberg Bridge Problem, which is also called The Seven Bridges of Königsberg.
Königsberg, a
Prussian city that is now a part of
Russia and is known as
Kaliningrad, was bisected by the
Pregel River. This river has two large islands joined to each other and the rest of the city by seven bridges (see figure). The problem is to find a path crossing each bridge exactly once and returning to your arbitrary starting point in the city.
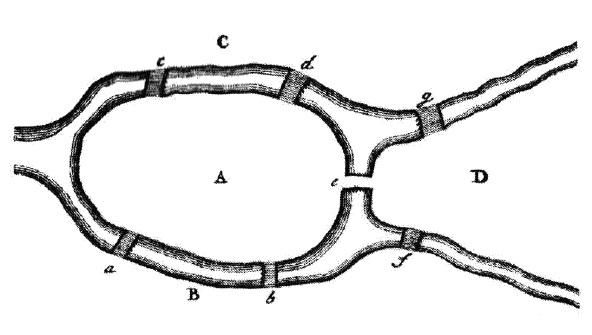
The Seven Bridges of Königsberg, from Euler's publication. Fig. 3 of Ref. 1, via arXiv.[1]
The problem was "solved" by
Euler, who showed that there was no solution. Euler realized that he could condense the problem into a
graph in which the land masses were
vertices and the connections between them (the bridges) are represented by connecting lines. Thus, choosing a vertex as the starting point, the only important action was the sequence in which the bridges are traversed. In this time before computers, Euler realized that an
exhaustive search was possible, although difficult. This would be very similar to the computer proof of the
Four Color Conjecture. Wrote Euler,
"The particular problem of the seven bridges of Königsberg could be solved by carefully tabulating all possible paths, thereby ascertaining by inspection which of them, if any, met the requirement. This method of solution, however, is too tedious and too difficult because of the large number of possible combinations, and in other problems where many more bridges are involved it could not be used at all." [1].
So, Euler decided to think about the problem, instead. This points out one difference between Euler and me. I would have jumped to my keyboard and started writing a program, since I find thinking to be very difficult. His first observation was that every time you reach a vertex by a bridge, you need to exit the vertex by another bridge. After a little thought, you realize that the number of connections to each vertex must be even if no bridge is traversed twice. You see that there are four land masses (four vertices), one of which has five connections, and the other three have three connections. So, Euler's 1736 resolution of this problem is that such a path (now called an
Eulerian circuit) does not exist. In
contemporary mathspeak,
A connected graph G = (V,E) contains an Eulerian circuit if and only if the degree of every vertex v ∈ V is even.[2]
where the graph G is specified by its
set of vertices (V) and set of edges (E), and each vertex v is a member of V
There's another piece of mathematics, called the
St. Petersburg paradox, that has as much to do with
economics and
psychology as it does with math. The
paradox was named by
Daniel Bernoulli, who published it and his solution in 1738; but he had heard it many years earlier from a cousin,
Nicolas Bernoulli. Anyone in math or physics knows that there were many important Bernoullis, and they're interchangeable in most discussions, since no one can keep track of who is who. The paradox relates to a particular
lottery and how much you would be willing to pay for a ticket. This lottery is quite different from the usual games of chance, so the
odds calculation is, to say the least, unusual. Here's the way the lottery is played.
1) at each stage of game play, a fair coin is tossed.
2) On heads, the lottery pays $1, and the game ends. On tails, the coin is tossed again.
3) On heads, the lottery pays $2, and the game ends. On tails, the coin is tossed again.
...
n) On heads, the lottery pays $2(n-1), and the game ends. On tails, the coin is tossed again.
At first glance, I might be willing to pay two dollars for a lottery ticket, since it seems as if this process is a little better than a simple coin toss with 50:50 odds when taken to the second step; that is, I could loss a dollar, but I might win two dollars. Bernoulli showed how wrong my approximation of the odds can be. The
expected value of the payout is easy to calculate by multiplying the winnings by the probability of winning at each stage and summing; viz.,
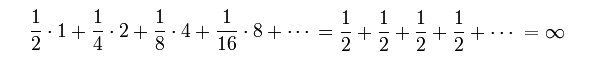
In short, this is a lottery you can't lose if you play an
infinite number of rounds; but what if you're not that patient, or don't have a lot of money? Does it still make sense to play?
As would any computer person, I decided to
simulate this game with a simple program (C source code
here). The figure below shows the results of 10,000 trials of 10,000 games each. This would approximate the payout if you bought a ticket each day for twenty-seven years.
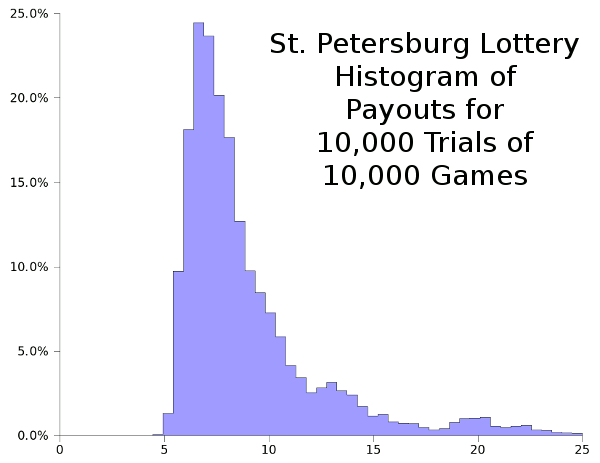
Histogram of payouts for 10,000 trials of 10,000 games of the St. Petersburg Lottery. Data analysis via Gnumeric.
If you're willing to play 10,000 games, a $5 ticket would be a good bet, since it would be a rare case that you would lose any money. Note, however, that if your payout averages $4.90 per game, you'll be out a thousand dollars in the end. However, if you are able to hit the peak of the histogram, you'll make about $20,000 with those $5 tickets, with a chance that you'll get a huge payout, perhaps $100,000, in the
long tail.
So, what lesson can be learned from this? The mathematical result of infinite winnings, although seductive, would apply only for infinite play. The mathematical prediction that the lottery is worth playing at any price is flawed. In real life, if you're interested in a sure thing, you shouldn't pay more than $5 for such a ticket. Various analyses of this paradox are iterated on
Wikipedia.[4]
References:
- L. Euler, "Solutio problematis ad geometrian situs pertinentis," Comm. Acad. Sci. Imper. Petropol.," vol. 8, pp. 128-140, 1736 (as cited in Ref. 3).
- Stephan Mertens, "Computational Complexity for Physicists," arXiv Preprint, April 7, 2002.
- Ole Peters, "The time resolution of the St. Petersburg paradox," arXiv Preprint, November 19, 2010.
- St. Petersburg Paradox Page on Wikipedia.
- Anders Martin-Löf, "An analysis of two modifications of the Petersburg game," arXiv Preprint, December 27, 2007.
Permanent Link to this article
Linked Keywords: Physics; mathematical theorem; Pythagoras; Pythagorean theorem; Königsberg Bridge Problem; Prussian; Russia; Kaliningrad; Pregel River; The Seven Bridges of Königsberg; Euler; graph; vertex; graph_theory; brute-force search; exhaustive search; Four Color Conjecture; Eulerian circuit; Newspeak; set; St. Petersburg paradox; economics; psychology; paradox; Daniel Bernoulli; Nicolas Bernoulli; lottery; odds; fair coin; expected value; infinite; simulate; Gnumeric; long tail; Wikipedia; arXiv.