| Tikalon Blog is now in archive mode.
An easily printed and saved version of this article, and a link
to a directory of all articles, can be found below: |
|
This article |
| Directory of all articles |
General Relativity Test
October 7, 2010
One of the more interesting consequences of
Einstein's theory of
special relativity is the
Twin Paradox. Although this effect is commonly known as a "paradox," Einstein considered it to be just a natural consequence of his theory. The bland, physics explanation of the theory has our
synchronizing clocks. We then send one on a long trip that returns it to the other clock, and when we recheck the clocks, the time on the traveling clock will lag that of the stationary clock. The amount of lag will depend on how fast the clock had moved and for how long. This has been proven by many experiments, some of which have used
radioactive decay as the clock. Because of such experiments, we're all fairly confident that this "theory" is a "fact," at least in the
common sense understanding of the word.
In 1911, shortly after publication of the theory,
Paul Langevin made the clock effect more interesting by giving it a human face. Humans are
chemical factories, and
chemical reaction rates will respond to relativity just like everything else. Langevin did not mention twins, but he did have a traveler make a two year trip at nearly the speed of light. Two years, that is, on his clock. Two hundred years had passed on Earth when he returned. For a thorough explanation of the paradox, along with many equations, I refer you to the Wikipedia entry.[1]
As I mentioned, special relativity has been proven experimentally many times over in many diverse experiments.
One of these, in 1972, involved flying four
atomic clocks on commercial jetliners around the world, some eastward and some westward, and then comparing their times with a stationary clock.[2-3] Theory predicted that the eastward clocks should have lost 40±23 nanoseconds, and the westward clocks should have gained 275±21 nanoseconds. The experimental results were 59±10 nanoseconds and 273±7 nanoseconds. Needless to say, even with the
frequent flyer miles, this was an expensive experiment; but relativity is one of those things that's hard to believe without proof. The
Global Positioning System was operational a year after this experiment, and it's interesting to note that the GPS satellite clocks
need to correct for special relativity.
An experiment reported in a recent issue of
Science brings a measurement of this type down to Earth by using extremely accurate clocks.[4-6] These clocks, which have a fractional frequency accuracy of 8.6 x 10
-18, are based on a 1.121
Petahertz (1.121 x 10
15) transition of
laser-cooled aluminum (Al
+) ions (see figure).[7] These clocks were developed by a research team at the
Time and Frequency Division of the
National Institute of Standards and Technology (NIST,
Boulder, Colorado). What does this accuracy get you when you want to test relativity? It means that you don't need to use jet airliners and wait weeks for your data. You can do a relativity experiment in a single laboratory by just having one clock a little higher than the other.
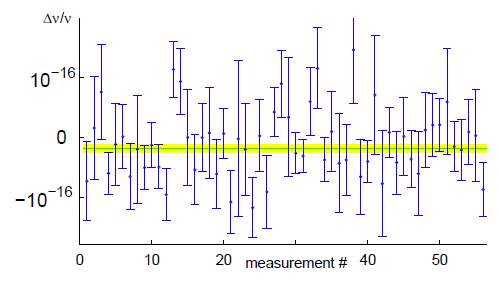
Fractional frequency difference between the two NIST Aluminum atomic clocks (via arXiv, Ref. 7). The error bars indicate a standard deviation.
Well, not exactly a single laboratory, but a pair of laboratories connected by a 75-meter
optical fiber.[4,5] In this case, the clocks are stationary, and what's being tested is not special relativity, but the larger theory of which special relativity is a subset; namely,
general relativity. General relativity predicts
time dilation effects caused by
gravitation. In the NIST experiment, the difference in altitude between the two atomic clocks was just 33 cm, but the difference in gravitational field was enough to show that clocks at lower altitude lag behind their higher altitude twins. The altitude affect is vanishingly small. As the authors state in their paper, a clock two-thirds of a mile above an identical clock on Earth's surface will speed up by only three seconds in a million years.[6] Using this estimate, and doing the math for a foot difference in altitude, gives a fractional change of 2.7 x 10
-17, which is just within the range tested by the NIST clock. This is definitely
leading edge physics.
References:
- Twin Paradox Page on Wikipedia.
- J. C. Hafele and Richard E. Keating, "Around-the-World Atomic Clocks: Predicted Relativistic Time Gains," Science, vol. 177, no. 4044 (July 14, 1972), pp. 166-168.
- J. C. Hafele and Richard E. Keating, "Around-the-World Atomic Clocks: Observed Relativistic Time Gains," Science, vol. 177, no. 4044 (July 14, 1972), pp. 168-170
- C. W. Chou, D. B. Hume, T. Rosenband, D. J. Wineland, "Optical Clocks and Relativity," Science, vol. 329, no. 5999 (September 22, 2010), pp. 1630-1633.
- Laura Ost, "NIST Pair of Aluminum Atomic Clocks Reveal Einstein's Relativity at a Personal Scale," NIST Press Release (September 23, 2010).
- Eryn Brown, "Ultraprecise clock helps cut relativity down to size," Los Angeles Times, September 25, 2010.
- C.-W. Chou, D. B. Hume, J. C. J. Koelemeij, D. J. Wineland and T. Rosenband, "Frequency Comparison of Two High-Accuracy Al+ Optical Clocks," ArXiv Preprint (February 2, 2010.
Permanent Link to this article
Linked Keywords: Einstein; special relativity; Twin Paradox; synchronization; radioactive decay; common sense; Paul Langevin; chemical factories; chemical reaction rates; Hafele-Keating experiment; atomic clocks; frequent flyer miles; Global Positioning System; gravitational time dilation; Science; Petahertz; laser-cooled; aluminum; Time and Frequency Division; National Institute of Standards and Technology; Boulder, Colorado; optical fiber; general relativity; time dilation; gravitation; leading edge.