| Tikalon Blog is now in archive mode.
An easily printed and saved version of this article, and a link
to a directory of all articles, can be found below: |
|
This article |
| Directory of all articles |
Math Counts
December 1, 2010
MATHCOUNTS is an organization that promotes mathematics for students in the
middle school grades (6-8). It was founded in 1984 by the
National Society of Professional Engineers, the
National Council of Teachers of Mathematics and the
CNA Foundation, and it receives financial support from donations by corporations, foundations and individuals. It sponsors mathematics competitions and has more than half a million registered students. One of the more interesting places on its web site, at least for students, is the
Problem of the Week. These are word problems that are crafted to be interesting; and during holiday seasons, the problems have a holiday theme.
In the early years of MATCHCOUNTS, I contributed a few problems of the week. This was so early in its history that they are not included in their web site archive. and they cannot be found via an internet search. I've posted three of them here, one of which relates to the upcoming year-end holidays. Try these on your precocious children/grandchildren/nieces/nephews. The answers are found below.
Trash Pickup
My township reduced its trash pickup from five days a week to four days a week, eliminating Friday pickup. Instead of just allocating a quarter of Friday's customers to each of the other four week days, they kept the same pickup circuit and shifted customers earlier in the week, as required. The first scheme of shifting Friday customers to other days would have just changed the pickup day for 20% of the people. What percentage of people will have their pickup day changed in the second scheme in which the order of pickups remains the same?
Holiday Baking
Marianne is baking a holiday bread, and the recipe calls for melting a stick of butter in a saucepan of milk. This seems to be taking a long time. Her older brother, Michael, tells her that if she had cut the butter into smaller pieces, it would melt faster, since more surface area is in contact with the warm milk. A stick of butter has dimensions 1" x 1" x 4-1/2" and it can be cut across the long edge into eight tablespoon-sized portions. What would be the increased surface area when a butter stick is cut into eight tablespoon-sized portions?
Ancestors
I have two parents, who also had two parents (my four grandparents), who also had two parents (my eight great-grandparents), etc. Civilization existed at least as far back as the Egyptian pyramids (4500 years before I was born), and a human generation is about 20 years. How many ancestors did I have at that time?
Now, the answers.
Answer: Trash Pickup

Trash schedule problem)
With reference to the figure, you can see that the number of customers on Monday-Friday must be increased by 25% to compress five days into four. When we shift customers around the circuit, 1/4 of Tuesday's original customers are bumped to Monday; half of Wednesday's original customers are bumped to Tuesday; three-quarters of Thursday's original customers are bumped to Wednesday, and all of Friday's original customers are bumped to Thursday. Adding things up, we find that half of all customers have trash pickup on a different day.
(1/4 x 1/5) + (1/2 x 1/5) + (3/4 x 1/5) + (1 x 1/5) =
(1/5)(2½) = 1/2, or 50%
Answer: Holiday Baking
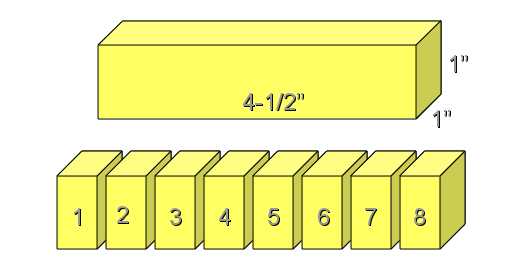
Butter problem. Each slice adds two square inches of area.
An uncut stick of butter has the following area
(1 x 4½) + (1 x 4½)+ (1 x 4½)+ (1 x 4½) + (1 x 1) + (1 x 1) = 20 sq. in.
Each cut exposes two extra square inches of area, and seven cuts are needed to slice the stick into eight pats of butter. Calculating the percentage increase yields
( (20 + (2 x 7))/20) = (34/20) = 1.70 = 170%, or a 70% increase.
Answer: Ancestors
This is a simple exponential sequence (think of the
wheat and chessboard problem, or its many variants). Dividing 4500 by twenty gives us 225 generations. The first generation back is, of course, 2
1, or my two parents. The next generation back is 2
2, or my four grandparents. Two hundred and twenty-five generations back is
2225 = 5 x 1067
This huge number indicates that there were many more people alive in the past than today. How can you explain that?
References:
- MATHCOUNTS Page on Wikipedia.
- This Blog, "Exponential Vampires," October 30, 2006.
Permanent Link to this article
Linked Keywords: MATHCOUNTS; middle school; grades (6-8); National Society of Professional Engineers; National Council of Teachers of Mathematics; CNA Foundation; Problem of the Week; wheat and chessboard problem.