| Tikalon Blog is now in archive mode.
An easily printed and saved version of this article, and a link
to a directory of all articles, can be found below: |
|
This article |
| Directory of all articles |
Fine Structure Constant
September 16, 2010
In a
recent article (Radioactive Decay, August 30, 2010), I wrote about anomalies in radioactive decay that might be caused by the sun; and one possible explanation being that the Sun may produce a field that changes the value of the
fine structure constant. I wrote that any change in the fine structure constant seems unlikely, since the fine structure constant agrees with
theory to eleven decimal places. The fine structure constant is related to some rather fundamental things; namely, the
elementary charge e,
Planck's constant h, the
speed of light c and the mathematical constant
π,
α = (2 π e2)/(h c)
where
α is the
dimensionless fine structure constant. This constant, which is quite close to the reciprocal of 137 (~1/137.036), expresses the strength of the interaction of charged particles, and it's fundamental to
electromagnetism. So, if
α changes, is it because
e,
h or
c changes? As one of my
Romanian scientist acquaintances would often state, "No such way!"
Finding such a local change in the fine structure constant would be quite unusual, but there has always been speculation that the constant could have changed over cosmological times. Any change, however, can't be too large, or life would not exist in our universe. The omnipresent
Anthropic Principle can be applied to the value of the fine structure constant. If α were too far off its mark, stellar fusion would not produce any carbon, and I wouldn't be here to write this article. Other explanations of the value of this constant have been attempted.
Sir Arthur Eddington, who was famous for his observations of the
solar eclipse of May 29, 1919 that confirmed
Einstein's theory of
general relativity, was
fascinated by the closeness of the reciprocal to the number 137. Eddington used it in a
numerological theory to derive the number of
protons in the universe, and his research in this direction was parodied by none other than
Hans Bethe.[1]
A paper [2-4] just submitted to
Physical Review Letters by astronomers at the
University of New South Wales in
Sydney, Australia, gives some evidence that the constant may have changed over cosmological time. The researchers measured the
spectra of
quasars visible in the northern and southern hemispheres. What was measured was not the emitted light of the quasars, but the absorption lines in the intervening gas clouds that permeate the universe. The northern hemisphere measurements were done using the
Keck telescope,
Mauna Kea, Hawaii; and the southern hemisphere observations were done using the
European Southern Observatory Very Large Telescope,
Cerro Paranal, Chile. Their data showed a smaller value of α when looking at one side of the universe ("north"); and a larger value of α when looking at the opposite side of the universe ("south"). The claimed validity of their data is 4.1 sigma, and they even give a vector of the "alpha dipole;" namely,
right ascension 17.3 +/- 0.6 hours,
declination -61 +/- 9 degrees.
Temporal evolution of the universe (NASA).
The 4.1 sigma of their data is impressive, since it indicates only a 0.6% chance that the result is random. As an added measure of confidence, six quasars were observable with both telescopes.[2,3] Nonetheless, their measured α at an age of the universe 9 billion years ago was only 0.0006% smaller.[2,4] There are naysayers. Astronomers at the
University of California, San Diego, submitted a paper to
The Astrophysical Journal[5] in which they claim that the Keck spectrometer has too much drift to yield the precision the Australian team claims. As usual, only time will tell. I'm one who prefers that constants remain constant, but I was never very good with change.
A recent article by Giuseppe Dattoli, posted on the arXiv preprint server,[6] introduced me to the following "calculation" of the fine structure constant.[7]
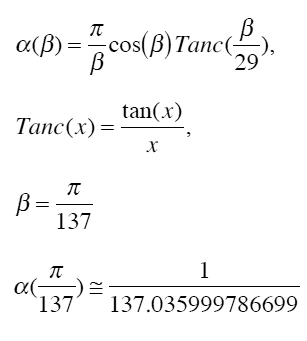
This value agrees quite closely with the accepted CODATA 2007 value of 1/137.035 999 679.[8]
References:
- G. Beck, H. Bethe, and W. Riezler, "Remarks on the quantum theory of the absolute zero of temperature," (in German), Die Naturwissenschaften, vol. 2 (1931), pp.38-9. (referenced as volume 19 in another source.)
- The Fine-Structure Constant and the Nature of the Universe, The Economist, August 31, 2010.
- Ron Cowen, "Changing one of nature's constants," Science News, September 3, 2010.
- J. K. Webb, J. A. King, M. T. Murphy, V. V. Flambaum, R. F. Carswell and M. B. Bainbridge, "Evidence For Spatial Variation of the Fine Structure Constant," arXiv, August 23, 2010.
- Jonathan B. Whitmore, Michael T. Murphy, Kim Griest, "Wavelength Calibration of the VLT-UVES Spectrograph," arXiv, April 20, 2010.
- Giuseppe Dattoli, "The fine structure constant and numerical alchemy," arXiv (September 9, 2010).
- James G. Gilson, "The Case for the Fine Structure Constant Approximation," October 14, 2003.
- Peter J. Mohr, Barry N. Taylor and David B. Newell, "CODATA Recommended Values of the Fundamental Physical Constants: 2006," arXiv (December 29, 2007).
Permanent Link to this article
Linked Keywords: Radioactive decay; fine structure constant; quantum electrodynamics; elementary charge; Planck's constant; speed of light; pi; dimensionless; electromagnetism; Romanian; Anthropic Principle; Sir Arthur Eddington; solar eclipse of May 29, 1919; Einstein; general relativity; Eddington number; numerological; protons; Hans Bethe; Physical Review Letters; University of New South Wales; Sydney, Australia; astronomical spectroscopy; quasars; Keck telescope; Mauna Kea, Hawaii; European Southern Observatory; Very Large Telescope; Cerro Paranal, Chile; right ascension; declination; University of California, San Diego; The Astrophysical Journal.