| Tikalon Blog is now in archive mode.
An easily printed and saved version of this article, and a link
to a directory of all articles, can be found below: |
|
This article |
| Directory of all articles |
Fat Protons
July 12, 2010
Many years ago, the American Physical Society had a Physics Limerick Contest. Among the entries I submitted was this [1]
Hadrons, leptons, bosons, too,
Are members of our little zoo.
Though in their stalls
As little balls,
They're really clouds of quantum goo.
This limerick highlights the fact that the elementary particles that we visualize as perfect spheres are nothing of the sort. Since they are localized in space for some reason, we give them an arbitrary radius called the root-mean-squared charge radius, a compromise which takes into account that not all the charge is contained in a tidy sphere. The acknowledged best value for the proton radius[2] is 0.8768 x 10
15 meter with an uncertainty of about 0.78%. We may need to revise this number downwards to 0.84184 x 10
15 meter as a result of a recent experiment.[3-7] If confirmed, this revised measure of the proton size might require modification of the so-called
Standard Model of particle physics. What's especially interesting is that this new value of the proton radius will increase the charge density of protons by about thirteen percent.
A cover story in the recent issue of
Nature derives this new value from pulsed laser
spectroscopy of the
Lamb shift of electron energy levels in muonic hydrogen (a proton orbited by a negative
muon). Muonic hydrogen provides a better testbed than hydrogen. This is because the muon "travels"[8] nearer to the proton than an
electron, since it has about 200 times the mass. The significance of this paper is attested not only by its cover status, but also by the number of authors - thirty-three!
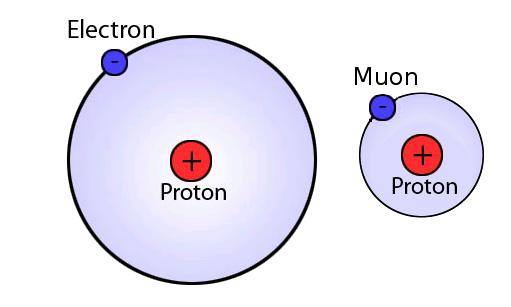
Bohr models of normal and muonic hydrogen.
Hydrogen is the most abundant element in the universe, and since hydrogen is composed of just a single proton with an electron, that makes the proton the most abundant
hadron in the universe. Why the proton has its particular charge radius and its particular magnetic moment is unknown. Because of the simplicity of the hydrogen atom, most quantum mechanical calculations are done using hydrogen. This includes
Quantum Electrodynamics (QED), a theory that's been found to agree with experiment to 10 parts per billion. The standard model, which attempts to predict all properties of matter except gravitational attraction, was constructed using hydrogen as a reference.[4]
The muonium experiment is based on a property of hydrogen called the
Lamb shift. The Lamb shift is the small difference in energy between two electron, or muon, orbitals that should have the same energy. They don't because the electrons and muons interact with
vacuum states. It's possible to calculate the proton radius using the measured Lamb shift, and the group that did the muonium measurement used intense laser radiation to do that. The research was conducted by a huge international team led by Randolf Pohl of the
Max-Planck Institute for Quantum Optics, near
Munich, Germany. The major problem Pohl's team overcame was that muons exist for just two milliseconds, so they needed to create muonium and measure it immediately.[4] The research team was able to create a few hundred muons each second, and just a few replaced the electrons in a background of hydrogen gas and interacted with the laser before they decomposed.[5] One interesting thing was that the physicists had tuned their apparatus to detect a proton radius close to the established value, and they got no signal. Only by broadening their experimental parameters did they get a result.[7]
Jeff Flowers, a physicist at the
National Physical Laboratory,
Teddington, England, writes in the same issue of Nature[8] that there are three possible interpretations of the Max-Planck result[4]:
1. There is some mistake in the experiment. One internet commentary says that replacing electrons with muons might not be strictly equivalent, and it may be a faulty assumption.
2. The calculations that derive the proton radius from the Lamb shift might be incorrect. For example, there's an error in the Rydberg constant, which is used in the equation.[6]
3. The Standard Model is not accurate.
Are protons getting thinner? Until this experiment is replicated, and the issues that Flowers lists are resolved, we won't know. Several years will pass before a consensus emerges. The answer may lead to some new physics.
References:
- Physics Limericks-Devlin Gualtieri
- NIST, "CODATA Value: proton rms charge radius".
- Randolf Pohl, et al., "The size of the proton," Nature, vol. 466, no. 7303 (July 8, 2010), pp. 213-216.
- Thomas H. Maugh II, "Physics: Proton radius smaller than believed, European scientists say," Los Angeles Times Online, July 7, 2010.
- Lisa Grossman, "'Horrendously Intense' Laser Shrinks the Proton," Wired, July 7, 2010.
- Rachel Ehrenberg, "The incredible shrinking proton," Science News Online, July 7, 2010.
- Kate Ravilious, "Proton Smaller Than Thought-May Rewrite Laws of Physics," National Geographic Online, July 7, 2010.
- Once again, we succumb to a simple model. The muon is everywhere around the proton. It does not travel in an actual orbit, although it has a higher probability of being nearer than an electron to the proton.
- Jeff Flowers, "Quantum electrodynamics: A chink in the armour?" Nature, vol. 466, no. 7303 (July 8, 2010), p. 195.
Permanent Link to this article