| Tikalon Blog is now in archive mode.
An easily printed and saved version of this article, and a link
to a directory of all articles, can be found below: |
|
This article |
| Directory of all articles |
Buffon's Needle
July 19, 2010
I've had a lifelong fascination with the constant, pi. Pi is not only an important part of mathematics, it's an important part of physical reality, since many equations of physics involve pi. For example, the
Einstein field equations of
general relativity contain the constant (8πG/c
4).
In a
previous article (Infinite Series Expressions, August 14, 2008), I listed these series for calculating pi:
π/4 = 1 - (1/3) + (1/5) - (1/7) + (1/9) - (1/11) ...
π
2/6 = 1 + (1/4) + (1/9) + (1/16) + (1/25) + (1/36) ...
Although pi can be computed from these series, it converges rather slowly, so it takes a long time to get a good value for pi.
Another series, developed by the brothers,
David Chudnovsky and
Gregory Chudnovsky, delivers three digits of pi per calculated term,
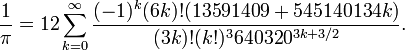
The Chudnovsky algorithm is a variation of one discovered by the mathematics prodigy, Srinivasa Ramanujan.
Georges-Louis Leclerc, Comte de Buffon, was a polymath who contributed to many scientific disciplines in the eighteenth century, including physics and biology. He also devised a physical method of estimating the value of pi that didn't involve a measurement, such as unwinding a circle and ratioing it against its diameter. Buffon's method merely involved dropping a needle repeatedly onto a floor. Not just any floor, but a floor with slats that are the same width (d) as the length of the needle (l) (see figure). All an observer needs to do is to count how many times the needle crosses a crack between the floor slats. The needle either falls across a crack (case "a"), or doesn't (case "b").
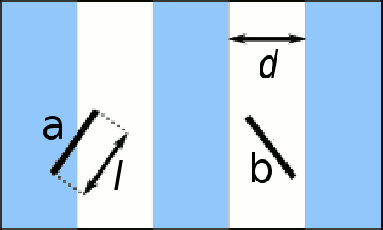
Buffon's Needle
Pi is calculated as twice the ratio of total needle drops to the number of times the needle bridges a crack. So, can we get a good value of pi using Buffon's method? I'm not ambitious enough to drop a needle thousands of times and record the results, so I had two choices. I could build a machine to do that for me, or I could write a computer simulation. The first choice is an interesting project, and I may try that some day, but the second choice was very easy. You can examine my C-language program,
here. I used the program to run 10,000 trials of 100,000 needle drops each. The results followed a normal distribution (see figure), giving a mean of 3.1415190247, and a standard deviation of 0.00745718421118. Although the mean appears very close, statistically, this result means that we can be 95% confident that the value of pi lies between 3.126604656 and 3.156433393. Not very good at all.
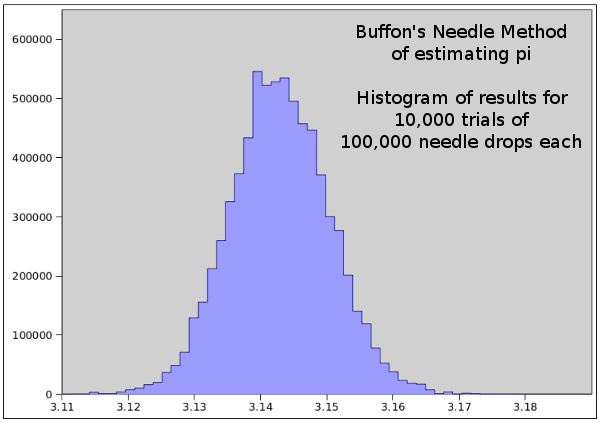
Histogram of results for 10,000 trials of 100,000 Buffon Needle drops.
References:
- Buffon's needle on Wikipedia.
- Numerical Approximations of Pi.
- The Joy of Pi.
- Pi Formulas on Mathworld.
- Animation of Buffon's Needle.
- Buffon's Needle Simulation.
Permanent Link to this article