Drawing Lots
January 9, 2023
Julius (Groucho) Marx (1890-1977) famously stated, "
I don’t care to belong to any club that will have me as a member."
Nobel Physics Laureate,
Richard Feynman (1918-1988), had a different
motive for his resignation from the
US National Academy of Sciences. Feynman was by his nature against
elitist organizations, and he resigned "because there was another organization most of whose time was spent in choosing who's illustrious enough to be allowed to join us..."[1]
Long before
paper ballots and
hanging chads,
voting was accomplished in
ancient Greece through the use of readily available
pebbles.
Greeks were a
seafaring people, as
Homer's Iliad and
Odyssey document, so there must have been an abundance of
polished stones along the
sea coast. Votes were cast by
actually casting a pebble into an
urn, a white pebble signifying a
yes vote, and a black pebble signifying a
no vote.

"Yea," or "nay." Polished white and black quartz pebbles.
Pebbles polished by flowing water, as in rivers and along coastlines, are not polished by the water, itself, but by sediments in the water. minerals of a certain Mohs hardness will be polished by minerals with the same or greater hardness.
(Portions of a Wikimedia Commons image by Mauro Cateb.)
Starting in the
19th century, some
social organizations used a variant of this same pebble process. In a
technological advance over pebbles, white and black
marbles were used, and
majority voting for admission of a new member was replaced by a process called
blackballing. If just a single member objected, his solitary black marble was cause enough to reject an applicant.
This introduction brings us to the
mathematics of drawing marbles at
random from an urn containing an equal number of white and black marbles. In such a process, what's the
probability of obtaining a
streak of drawing
n black marbles before a white marble is drawn? It's easily seen that the probability of getting a black marble at the first draw is 1/2, two black marbles in two draws is 1/4, etc., giving a simple
geometric series. To get a true geometric series, a marble must be replaced after it's drawn. Alternatively, having a large number of marbles in the urn will give a good
approximation if the drawn marbles are not replaced. The
computer simulation of this is quite simple, and I give a
C language program here with results shown in the figure.
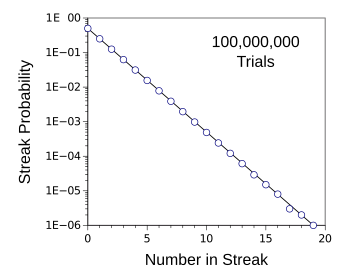
Plot showing the probability of getting a streak of n black marbles pulled from an urn before a white marble is drawn.
This exponentially decaying function is best displayed on a semilog plot, as shown, since the probabilities descend quite rapidly.
These are data for a hundred million trials simulated with my C language program.
(Created using Gnumeric. Click for larger image.)
Semilog plots, such as the one above, are familiar to
chemists, since they are used in the
analysis of
reaction rate constants. The
Arrhenius rate equation, another exponential function, is
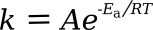
in which
k is the
rate constant,
A is a
pre-exponential factor,
Ea is the
activation energy,
R is the
gas constant, and
T is the
absolute temperature. Plotting the
natural logarithm of the rate constant against the
reciprocal of the absolute temperature (1/T) gives a
straight line whose
slope is
Ea/R and the
intercept at
1/T = 0 is the natural log of
A.
Svante Arrhenius (1859-1927) was
awarded the 1903
Nobel Prize for Chemistry for the
theory of
chemical equilibrium behind this simple
equation.
The
complement of exponential decay is
exponential growth in which each successive term is
proportionately greater. A common example of this is the
wheat and chessboard problem in which one
grain of
wheat is placed on the first
square, two on the second, four on the third, and so on. The total number of grains of wheat thus placed is
264 - 1, which is somewhat greater than 18
quintillion (US quintillion). This is sequence
A000079 in the
On-Line Encyclopedia of Integer Sequences.
While exponentially decaying function drop quite
precipitously, there's another type of function with a large
range on both plotted
axes. This is the
power law, given as
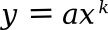
in which
a and
k are both
constants. Just as an exponential function is distinguished as a straight line in a semilog plot, a power law appears as a straight line in a
log-log plot. Examples of a power law are the
Stefan-Boltzmann law and the
inverse-square laws of
gravitational force and
electrostatic force.
An interesting example of a power law is
Zipf's law, named after
American linguist,
George Zipf (1902-1950). Zipf was the
popularizer of the law, not its
discoverer. Several
wrote about it before him, including
German physicist,
Felix Auerbach (1856-1933). Zipf's law states that in any
language the
frequency of use of any
word is
inversely proportional to its
rank in the list of word frequencies. In this power law, the probability of a word's occurrence is proportional to
(1/n); thus, the most frequent word will occur about twice as often as the second most frequent word, three times as often as the third most frequent word, and so on. The power law
exponent k for Zipf's law is
-1.
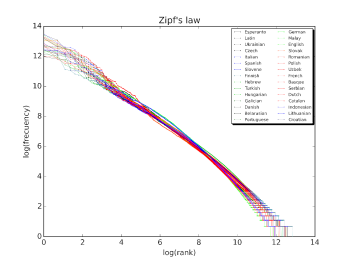
Zipf's law for Wikipedia.
This is a plot of the rank versus frequency for the first 10 million words for 30 language versions of Wikipedia on October, 2015.
The straight line on this log-log plot shows power law behavior.
(Wikimedia Commons image by Sergio Jimenez. Click for larger image.)
Another example of power law behavior is
company size, as
indicated by the number of
employees. This has an exponent of 1.06. The number of
shares traded in a
stock exchange per
unit of time is a power law with and exponent of 1.5. The
distribution of
surnames in the
United States, as shown in the following plot, also follows a power law.[2]
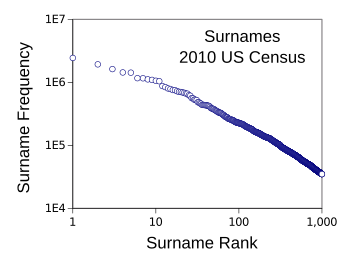
A plot of frequency vs rank for the first thousand surnames on the 2010 United States census showing power law behavior.[2]
The ten names of highest rank, in rank order, are Smith, Johnson, Williams, Brown, Jones, Garcia, Miller, Davis, Rodriguez, and Martinez. The three Hispanic names are an indication of the shifting demographics of the United States.
(Created using Gnumeric. Also uploaded to Wikimedia Commons. Click for larger image.)
Sabin Roman of the
Centre for the Study of Existential Risk of the
University of Cambridge (Cambridge, United Kingdom) and the
Odyssean Institute (London, United Kingdom), along with
Francesco Bertolotti of the
Carlo Cattaneo University (LIUC, Castellanza, Italy) have just
published a
paper on
arXiv in which they present an
algorithm for power law generation for drawing marbles from an urn.[3] The
trick is to add a large number of black marbles after every draw, thereby extending the
tail of the distribution.[3]
Their algorithm is as follows:[3]
• Select a constant K. In the authors' example, K = 1.5. Then select the number of white W and black B marbles. In my demonstration program these are each 1000.
• The number of black marbles is increased by W/K after each draw, and the draws continue until a white marble is drawn. Black marbles are replaced after they are drawn.
• When a white marble is drawn, W and B are reset to their original values.
The computer simulation of this is as simple as that for drawing marbles at random from an urn, as presented earlier. I give a C language program
here with results shown in the figure.
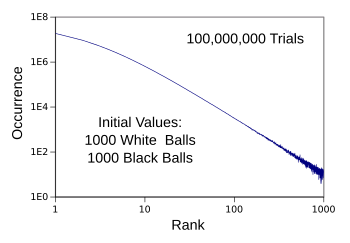
Computer simulation results for the power law algorithm of ref. 3.[3]
These are data for a hundred million trials simulated with my C language program.
(Created using Gnumeric. Click for larger image.)
References:
- Why Richard Feynman resigned from the National Academy of Sciences, Clip sourced from BBC "The Pleasure of Finding Things Out" (1981-1982), YouTube Video by Endless Analysis, Oct 30, 2022.
- Frequently Occurring Surnames from the 2010 Census, United States Census Bureau Website.
- Sabin Roman and Francesco Bertolotti, "A Master Equation for Power Laws," arXiv, October 13, 2022, https://doi.org/10.48550/arXiv.2210.09046.
Linked Keywords: Julius (Groucho) Marx (1890-1977); I don’t care to belong to any club that will have me as a member; Nobel Physics Laureate; Richard Feynman (1918-1988); motivation; motive; US National Academy of Sciences; elite; elitist; professional association; paper ballot; hanging chad; voting; ancient Greece; pebble; Greeks; seamanship; seafaring; population; people; Homer; Iliad; Odyssey; polishing; polished; rock (geology); stone; sea coast; cast; casting; urn; quartz; fluid dynamics; flow; flowing; water; river; coast; coastline; sediment; mineral; Mohs scale of mineral hardness; Mohs hardness; Wikimedia Commons; Mauro Cateb; 19th century; social; technology; technological; marble (toy); majority rule; majority voting; blackballing; mathematics; randomness; random; probability; winning streak; geometric series; approximation; computer simulation; C language program; drawing lots.c; plot (graphics); probability; exponential decay; exponentially decaying; function (mathematics); semilog plot; data; Gnumeric; chemist; analysis; chemical reaction; reaction rate constant; Arrhenius rate equation; rate constant; pre-exponential factor; activation energy; gas constant; thermodynamic temperature; absolute temperature; natural logarithm; multiplicative inverse; reciprocal; line (geometry); straight line; slope; y-intercept; Svante Arrhenius (1859-1927); award; awarded; Nobel Prize for Chemistry; scientific theory; chemical equilibrium<; equation; complement; exponential growth; proportionality (mathematics); proportionately; wheat and chessboard problem; food grain; wheat; square (geometry); names of large numbers; quintillion; A000079; On-Line Encyclopedia of Integer Sequences; precipitously; interval (mathematics); range<; Cartesian coordinate system; axis; axes; power law; constant (mathematics); log-log plot; Stefan-Boltzmann law; inverse-square law; gravitation; gravitational force; Coulomb's law; electrostatic force; Zipf's law; America; American; linguistics; linguist; George Zipf (1902-1950); popular science; popularizer; discovery (observation); discoverer; author; Germany; German; physicist; Felix Auerbach (1856-1933); language; statistical frequency; word; multiplicative inverse; inversely; ranking in statistics; rank; exponentiation; exponent; Wikipedia; plot (graphics); company; economic indicator; indicated<; employee; share (finance); stock trader; traded; stock exchange; unit of time; probability distribution; surname; United States; plot of frequency vs rank for the first thousand surnames on the 2010 United States census showing power law behavior; Hispanic; demographics of the United States; Gnumeric; Sabin Roman; Centre for the Study of Existential Risk; University of Cambridge (Cambridge, United Kingdom); Odyssean Institute (London, United Kingdom); Francesco Bertolotti; Carlo Cattaneo University (LIUC, Castellanza, Italy); scientific literature; publish; paper; arXiv; algorithm; methodology; trick; tail of the distribution; power law.c.