Thales' Measure of the Sun
June 26, 2023
Just one glance at the
periodic table or at one of the many
books on my
bookshelves reminds me that
science progresses by building upon prior
scientific discoveries. This
idea was expressed in the
metaphor written in a 1675
letter of
Isaac Newton (1642-1727) to
Robert Hooke (1635-1703),
"If I have seen further it is by standing on the sholders of Giants."
As you can see from the
word, "sholders," in the
quotation,
spelling was quite fluid in
Newton's time. This metaphor was used several
decades before Newton, when
Blaise Pascal (1623-1662), in his c. 1647
Preface to the Treatise on Vacuum, wrote about the knowledge we have gained from the
ancients:
"...Because having risen to a certain degree where they carried us, the slightest effort makes us rise higher, and with less pain and less glory we find ourselves above them."[1]
Scientists and
mathematicians of the past are sometimes
honored by the
naming of their notable discoveries after them. In recent
history, we have the
Planck constant, named after
German theoretical physicist,
Max Planck (1858-1947). Throughout history there have been many such
eponymous constants of nature, as detailed on
this Wikipedia Page, and there is also a
list of physical laws names after scientists.
One of the earliest examples of this in
mathematics is the
Pythagorean theorem, named after
Pythagoras of Samos (c.570-c.495 BC). Prior to that, however, is
Thales's theorem, named after
Thales of Miletus (c.625-c.546 BC). This
theorem, which is perhaps the first mathematical discovery, states that any
triangle inscribed in a
semicircle with one side as the
diameter is a
right triangle.

Thales, left, and Pythagoras. (Left image, an 1875 engraving of Thales by Wilhelm Meyer (1844–1944), based on a 4th century bust. Right image of Pythagoras from Wellcome Images, Library reference, ICV No 5031, Photo number, V0004825. Both from Wikimedia Commons. Of course, both are fanciful representations. Click for larger image.)
The most
distinguishing aspect of Thales is that he was the first of the
ancient Greek philosophers to embrace the idea that things happen, not through the
whims of
anthropomorphic gods, but according to
natural laws. In his quest for
first principles without the
knowledge of the world as we have it now, Thales believed that
water was the ultimate
building block of matter. Thales further thought that the Earth
floated in a vast body of water, an idea with variations throughout many
cultures, including one in which
the Earth is supported on the back of a giant turtle.
Thales measured the
heights of the
Egyptian pyramids using a technique involving
similar triangles by what's now called the
intercept theorem. He used the
shadow of the pyramid caused by the
Sun and the shadow of a
pole of a known height to get the
ratio of the pyramid height to that of the pole. He used the same method to find the distance from
shore to
ships at
sea.
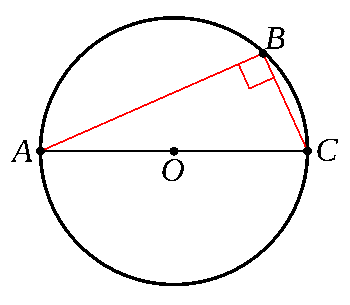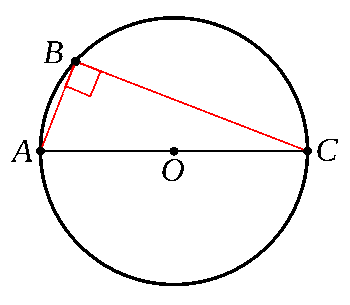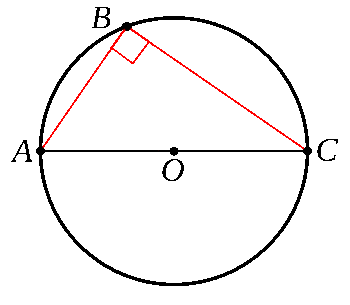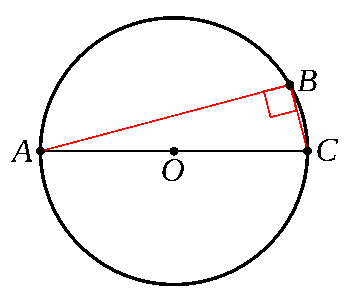
Thales's theorem that any triangle inscribed in a semicircle with one side as the diameter is a right triangle.
I was delighted when I first learned this in high school geometry.
(Created using Inkscape and GIMP.)
Thales was also
awarded the equivalent of the
Nobel Prize of his time. Bathycles, an
Arcadian sculptor and
architect, directed in his
will that a
gold tripod or
bowl should be given to him who had done most good by his wisdom. This item was passed among Thales and his fellow Greek
sages. Thales initially passed it along, but it was eventually agreed that it should go to Thales. He sent it to the
temple of Apollo at Didyma with the
dedication,
Thales the Milesian, son of Examyas [dedicates this] to Delphinian Apollo after twice winning the prize from all the Greeks.
A recent
paper by
Jorge Cuadra of the
Universidad Adolfo Ibáñez (Viña del Mar, Chile) at the
Publications of the Astronomical Society of Japan,[2] and also at
arXiv,[3] examines another of Thales' observations; namely the angular size of the Sun. As reported in 2nd and 3rd Century AD manuscripts. albeit far removed from his time, Thales was the first to measure the angular size of the Sun.[2-3]
Cleomedes (c. 2nd Century AD), described how to do this measurement by timing the duration of
sunrise, and it's suggested that Thales used the same method.[2-3] Cleomedes gives a size of 0.48°, just 10% smaller than the actual value of 0.5242-0.5422°.[2-3] Thales is reported by
Diogenes Laertius (c. 3rd century AD) to have obtained a value of
one seven hundred and twentieth part of the solar circle, which is 0.5°. Cuadra argues that uncorrected
error arising from the the variation of sunrise duration at different
latitudes and at different times of the
year is so large as to have prevented Thales from obtaining his roughly
accurate value.[2-3]
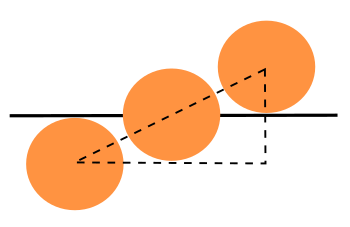
Illustration of sunrise with solar declination.
The maximum angle of declination, 23°26', occurs at the solstices. It's only at equinox that it's zero, and the Sun moves directly up from the horizon.
(Adapted from fig. 1 of ref. 3.[3] Click for larger image.)
One problem that Thales would have needed to surmount for a sunrise duration measurement was accurate
timekeeping. The only
clocks available to him were
water clocks. I addressed one source of inaccuracy of such clocks in a
previous article (Torricelli's law, January 23, 2017). Timekeeping problems aside, Cuadra argues that Thales did not have the ability to make the necessary
corrections to sunrise duration for latitude and declination to give his nearly flawless value. Corrections are required if the measurement is not done at the
equator during an equinox.
equation 4 of his paper illustrates this.[3]
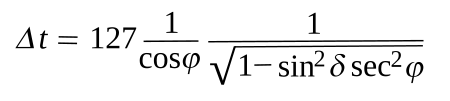
in which Δt is the duration of sunrise in
seconds, δ is the solar declination, and φ is the latitude. The range of sunrise duration for
Alexandria, where Thales visited, and
Miletus, his supposed home, is illustrated in the following
graph.
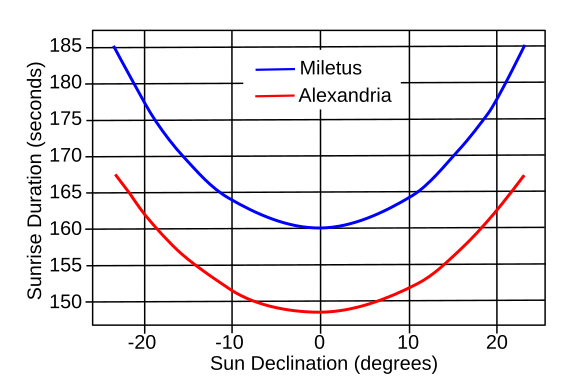
Duration of sunrise, Δt, in seconds, for the latitudes of Miletus (φ = 37.5°), and Alexandria (φ = 31.2°, as a function of solar declination. (Created using Inkscape from data in ref. 3.[3] Click for larger image.)
Thales would have had no idea of the concept of latitude; so, such a correction would be beyond his capability.[3] However, Cleomedes, living seven centuries after Thales, could have applied such a correction.[3] Either Thales used a method different from the duration of sunrise, or his value was corrected before it was mentioned in the 3rd century AD texts.[3]
References:
- A better translation from the French than that on Wikisource.
- Jorge Cuadra, "The asymmetric sunrise effect on Thales' alleged measurement of the Sun angular size," Publications of the Astronomical Society of Japan, vol. psad026 (April 20, 2023), https://doi.org/10.1093/pasj/psad026.
- Jorge Cuadra, "The Asymmetric Sunrise Effect on Thales' Alleged Measurement of the Sun Angular Size," arXiv, Apr 21, 2023, https://doi.org/10.48550/arXiv.2305.06149.
Linked Keywords: Periodic table; book; bookcase; bookshelf; science; scientific discovery; idea; standing on the shoulders of giants; metaphor; letter (message); Isaac Newton (1642-1727); Robert Hooke (1635-1703); word; quotation; spelling; 17th century; Newton's time; decade; Blaise Pascal (1623-1662); Preface to the Treatise on Vacuum; Ancient Greece; ancients; scientist; mathematicians; honor; honored; eponym; naming of their notable discoveries after them; history; Planck constant; Germany; German; theoretical physics; theoretical physicist; Max Planck (1858-1947); eponymous; physical constant; constants of nature; list of scientific constants named after people; Wikipedia; list of physical laws names after scientists; mathematics; Pythagorean theorem; Pythagoras of Samos (c.570-c.495 BC); Thales's theorem; Thales of Miletus (c.625-c.546 BC); theorem; triangle; inscribed figure; semicircle; diameter; right triangle; engraving; Wilhelm Meyer (1844–1944); 4th century; bust (sculpture); Wellcome Images; Wikimedia Commons; fanciful; distinguish; distinguishing aspect; ancient Greek philosophy; ancient Greek philosophers; whim; anthropomorphism; anthropomorphic; Greek mythology; god; physical lawvnatural law; first principle; knowledge; water; water (classical element); building block of matter; buoyancy; float; culture; World Turtle; Earth is supported on the back of a giant turtle; height; Egyptian pyramids; similar triangles; intercept theorem; shadow; Sun; column; pole; ratio; shore; ship; sea; high school; geometry; Inkscape; GIMP; award; awarded; Nobel Prize; Arcadia (region); Arcadian; sculpture; sculptor; architect; will and testament; gold; tripod; bowl; wisdom; sage (philosophy); temple of Apollo at Didyma; dedication (art); Delphinian Apollo; scientific literature; paper; Jorge Cuadra; Universidad Adolfo Ibáñez (Viña del Mar, Chile); Publications of the Astronomical Society of Japan; arXiv; Cleomedes (c. 2nd Century AD); sunrise; Diogenes Laertius (c. 3rd century AD); error; latitude; year; accuracy and precision; accurate; solar declination; solstice; equinox; horizon; timekeeping; clock; water clock; correction; equator; equation; seconds; Alexandria; Miletus; Cartesian coordinate system; graph; Duration of sunrise at Miletus and Alexandria as a function of solar declination.