Strength of Materials
May 11, 2020
At a very early age,
children discover than some things, like
eggs, are very
fragile, while things such as
rocks are more likely to break things than to be broken themselves. Knowledge of the
strength of materials becomes useful in life when you're doing such things as deciding which objects you can stand on
safely to
replace a light bulb. Some people find that the topic of
material strength is so interesting that they become
mechanical engineers and
materials scientists.
I pondered the strength of materials in my
youth when my
bicycle hand brake (which I now
surmise as having been
die cast from
zinc)
fractured; but, I was more interested in
physics, and that's what I studied as an
undergraduate. Lack of physics
funding for
graduate students in the early
1970s forced me to explore options other than physics. At the suggestion of one of my physics
professors, I
pivoted into a materials science
Ph.D. program. As I like to
joke, a
physicist is the type of
scientist who tries to find
steel in the
periodic table. Some of the
course topics were quite foreign to me, but I began to acclimate. Eventually, there were quite a few things that captured my interest, such as
chemical thermodynamics.
After some
post-doctoral research, I accepted a position in
industrial research under the
directorship of one of the country's most prominent materials scientists,
J. J. (Jack) Gilman (1925-2009). Gilman started as a mechanical engineer, but received a Ph.D. in
physical metallurgy from
Columbia University (New York, New York). After spending time in various industrial research organizations, he became a professor of
engineering at
Brown University (Providence, Rhode Island) in 1960, and then a professor of physics and
metallurgy at the
University of Illinois in 1963.[1]
Gilman became director of the
Allied Chemical Materials Research Center in 1968, and he remained at Allied for somewhat more than a
decade.[1] At Allied, he promoted
research and development of the
solid state laser material,
Alexandrite (
chromium-
doped Chrysoberyl), and
metallic glasses for use as
core materials for
power transformers, and as
magnetic shielding. In his later career, Gilman served as director of the
Center for Advanced Materials at the
Lawrence Berkeley Laboratory and a member of the
Department of Materials Science and Engineering at
UCLA.[1]

J. J. (Jack) Gilman (right), and his office at the Allied Chemical Materials Research Center (left), circa 1975. Note the ashtrays on the desk, since many people were still smokers in the 1970s. It was in this office in 1977 that Jack and I had a gentleman scientists' disagreement about the existence of short-range order in metallic glasses.
Gilman published four books, more than 250 scientific papers, and 73 articles on industrial management.[1] His publications included a theory of ball lightning.[2] He was a fellow of the American Physical Society and the American Society for Metals in 1971, and a member of the National Academy of Engineering.[1]
(Photographs from Allied Chemical promotional materials. Click for larger image.)
Material strength is related to
scratch resistance. Testing a
diamond by scratching
glass is a
plot point in many old
detective novels and
B-movies, the
idea being that
glass jewelry won't scratch glass, but diamond will. This scratch test is useless, for more reason than the present complications of
cubic zirconia (yttria-stabilized zirconia, YSZ) being used in
jewelry that
simulates diamonds, and the presumed inferiority of
synthetic diamonds over natural diamonds. Many glasses, however, have always been able to scratch other glasses, and there are many other materials that will scratch glass.
Window glass has a
hardness of about 5.5, but there are other glasses with hardness up to 6.6, YSZ has a hardness of 8.0, and
YAG (yttrium aluminum garnet) has a hardness of 8.5.
The idea that harder materials will scratch softer materials was mentioned in
antiquity by
Theophrastus in his
treatise,
On Stones, and
Pliny the Elder in his
Naturalis Historia (77 AD), both of which have been mentioned in this
blog. The scratch test of
mineral hardness was placed on a
scientific basis in 1812 by
German mineralogist,
Friedrich Mohs (1773-1839), who created what's now called the
Mohs scale of mineral hardness. The Mohs scale is an
ordinal scale of minerals in which members of higher rank will scratch members of lower rank (see figure).
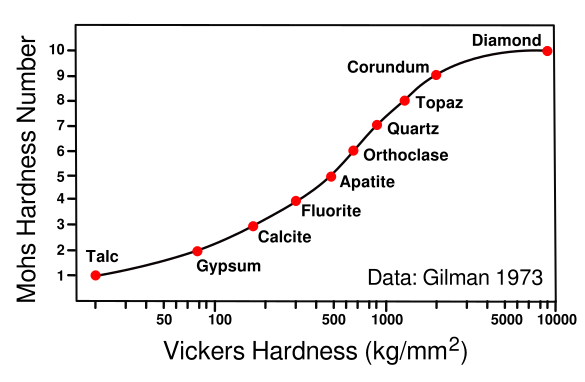
Relating hardness scales. The Vickers hardness test produces a material hardness number by pressing a pyrimidal indenter into the surface and measuring the dimensions of the indentation.
This graph relates Mohs hardness and Vickers hardness for the ten Mohs minerals, Talc, Mg3Si4O10(OH)2; Gypsum, CaSO4·2H2O; Calcite, CaCO3; Fluorite, CaF2; Apatite, Ca5(PO4)3(OH-,Cl-,F-); Orthoclase, KAlSi3O8; Quartz, SiO2; Topaz, Al2SiO4(OH-,F-)2; Corundum, Al2O3; and Diamond, C.
(Data from Gilman,[3] graphed using Inkscape. Click for larger image.)
At the most fundamental level, a material's strength arises from the
bonding energy that hold its
atoms together. In 1918, shortly after the
lattice structure of crystals was confirmed, German physicist,
Erwin Madelung (1881-1972),
calculated the
electrostatic forces that hold
ionic crystals together. The
calculation of this
lattice energy, which is -786
kJ/
mol for
NaCl, gives a
theoretical yield strength that's much larger than that observed. The theoretical yield strength, generally given in terms of
shear strength G (see figure), is
G/30, where G is the
shear modulus. The
experimental yield
stress of NaCl crystals can be as low as 1
MPa, while the theoretical value is 1000 MPa.[4]

Pull and tug - Visualization of tension (left) and shear (right) stress acting on a body. (Created using Inkscape)
The fact that actual materials are not ideal crystals is the reason behind this diminished strength. Crystals are imperfect at the atomic level, and this imperfection is manifested as
dislocations that allow easy glide across
crystal planes.
Polycrystalline materials and glass will have surface cracks that promote
fracture, and these might be as small as a scratch. In 1921,
aeronautical engineer,
Alan Arnold Griffith (1893-1963), conducted
experiments on
freshly-drawn glass fibers in which he added a controlled flaw, a
notch at the surface of the fibers.[5]
Griffith's data led to what's now called
Griffith's criterion, that for
brittle materials the
product of the stress at fracture and the
square root of the notch
length is nearly a
constant; that is,
σf√a ≈ C
where
σf is the stress at fracture,
a is the notch length, and
C is a constant that depends on the
energy required to create two new surfaces at each side of the fracture.
While
Diamond is at the top of the hardness scales, with a Mohs hardness of 10 and a Vickers hardness up to 150 GPa, materials scientists are on a quest for other
superhard materials that might be useful for
cutting tools and
wear-resistant coatings. Some limitations of diamond, aside from its high
cost, is that it
oxidizes at
temperatures above 800
°C and it's
inefficient in cutting
ferrous alloys since diamond
dissolves in
iron to form
iron carbides at high temperatures. Since the strength of diamond arises from its short, directional
covalent bonds between
carbon atoms, there's hope that similarly bonded compounds of low
atomic number elements like
boron, carbon,
nitrogen, and
oxygen will yield high hardness.
C
3N
4 and B-C-N
ternary compounds were the first of these materials to be investigated, followed by some
transition metal borides, such as ReB
2, OsB
2, and WB
4. In
theory,
beta-carbon nitride (β-C3N4) may be harder, but it has not been
synthesized.
Cubic boron nitride (β-BN) is nearly as hard as diamond; in fact, it will scratch diamond.
rhenium diboride (ReB2) is another material that scratches diamond.
Rhenium diboride is an excellent candidate for a superhard material, since the
electronegativities of
rhenium (1.9) and boron (2.04) are quite close, so their bonds have a mostly covalent character. The superhard properties of this material, which is synthesized at
ambient pressures, were discovered in 2007.[6]
Microindentation hardness tests showed an average hardness of 48 GPa, and
X-ray diffraction analysis gave a
bulk modulus of 360 GPa, which is not that much lower than that of diamond (445 GPa).[6-7] However, there are reasons to believe that diamond will all reign as the king of the superhards.[7]
While superhards will find application as
cutting tools, most useful high strength components are made from metal alloys, not
carbides and
borides. In an
open access paper in a recent issue of
Physical Review letters,
Michael Chandross and
Nicolas Argibay of
Sandia National Laboratories (Albuquerque, New Mexico), present a simple theory that allows prediction of the ultimate strength of pure metals and alloys.[8-10] Unlike most theories of this type, their theory does not need
fitting parameters.[10] It's based on
thermodynamics and the concept of
amorphization, and it closely predicts the ultimate strength of nearly 20 different metals (see graph).[8-10]
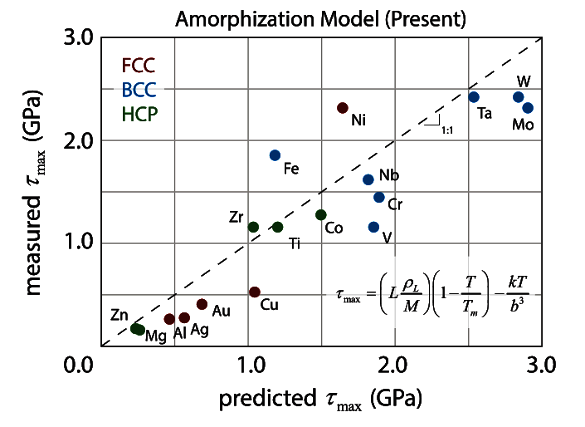
Sandia National Laboratories material shear strength model. (From fig. 3 of ref. 8, licensed under the Creative Commons Attribution 4.0 International license.[8])
Metals are
polycrystalline, being made from small crystal
grains that are bonded together at
grain boundaries that have an influence on their strength. The peak strength of a metals generally occurs for a grain size between 10-20
nm.[9] Large grains lead to
softer metals, since dislocations can more more easily. The
Hall-Petch law predicts that metal strength will increase as grain size is reduced,[11] but grains smaller than about 10 nm are associated with lower strength.[9] At about 10 nm, the grain boundaries become more important, and the conclusion is that the less
ordered nature of the grain boundary material is responsible, since
amorphous materials are softer.[9]
Chandross and Argibay developed a
model based on the
activation energy needed to cause
deformation by amorphization that predicts the peak strength of polycrystalline metals.[8] The model is based on material properties alone.[8] The model predicts the strength of the three principal crystal types,
body-centered cubic,
hexagonal close packed, and
face-centered cubicfcc, and also one alloy.[8] Chandross and Argibay make the
assumption that the energy needed to completely disorder a grain boundary is equal to the energy needed to
melt it, and this would be the activation energy for grain boundary sliding.[9] The result is an
equation for the strength of a metal in terms of its
melting point,
heat of fusion, and the
volume fraction of grain boundaries.[9]

Transformation of a crystalline metal (left) to an amorphous material (right), with an energy difference related to the heat of fusion. (Image from an American Physical Society Press Release, reformatted for clarity.[10])
Their model shows that the crystalline grains of a polycrystalline metal and its grain boundaries have equal strength near a grain size of about 10 nm, consistent with experiments.[9] These results might be extended to prediction of the
glass transition in polymers.[9] since the input parameters of the model are usually known, it should be possible to rapidly screen alloy compositions to determine the optimum grain size for maximum strength.[9]
References:
- John D. Mackenzie, "John J. Gilman 1925–2009," Memorial Tributes: Volume 14 (National Academies Press, 2011), pp.108ff..
- John Gilman, "Ball Lightning and Plasma Cohesion," arXiv, February 19, 2003.
- J. J. Gilman, "Hardness of pure alkali halides," Journal of Applied Physics, vol. 44, no. 3 (March, 1973), pp. 982ff., https://doi.org/10.1063/1.1662382.
- John J. Gilman, "Micromechanics of Shear Banding," Lawrence Berkeley Laboratory Report (August 1992), and the Proceedings of the Twenty-Ninth Annual Technical Meeting of the Society of Engineering Science (San Diego, CA, September 14, 1992), PDF file.
- A.A. Griffith, A. A. (1921), "The phenomena of rupture and flow in solids," Philosophical Transactions of the Royal Society of London, vol. A221 (1921), pp. 163–198. Available here, also.
- Hsiu-Ying Chung, Michelle B. Weinberger, Jonathan B. Levine, Abby Kavner, Jenn-Ming Yang, Sarah H. Tolbert, and Richard B. Kaner, "Synthesis of Ultra-Incompressible Superhard Rhenium Diboride at Ambient Pressure," Science, vol. 316. no. 5823 (20 April 2007), pp. 436-439.
- Vadim V. Brazhkin1,a) and Vladimir L. Solozhenko, "Myths about new ultrahard phases: Why materials that are significantly superior to diamond in elastic moduli and hardness are impossible," Journal of Applied Physics, vol. 125, no. 13 (April 3, 2019, Article no. 130901, https://doi.org/10.1063/1.5082739. Also at arXiv
- Michael Chandross and Nicolas Argibay, "Ultimate Strength of Metals," Phys. Rev. Lett., vol. 124, no. 12 (March 27, 2020), Article no. 125501, DOI:https://doi.org/10.1103/PhysRevLett.124.125501.
- Christopher A. Schuh, "Viewpoint: Deadlocked Order and Disorder in the Strongest Metals," Physics, vol 13, no. 4 (March 25, 2020)
- Ultimate strength of metals, American Physical Society Press Release, March 25, 2020.
- E O Hall, "The Deformation and Ageing of Mild Steel: III Discussion of Results," Proceedings of the Physical Society, Section B, vol. 64, no. 9 (September 1, 1951), pp. 747ff., https://doi.org/10.1088/0370-1301/64/9/303.
Linked Keywords:
Child; children; egg (food); brittleness; fragile; rock (geology); strength of materials; safety; lightbulb joke; replace a light bulb; materia; mechanical engineering; mechanical engineer; materials science; materials scientist; youth; bicycle; hand brake; surmise; die casting; die cast; zinc; fracture; fractured; physics; undergraduate education; funding of science; postgraduate education; graduate student; 1970s; professor; pivoted; Doctor of Philosophy; Ph.D.; joke; scientist; steel; periodic table; course (education); chemical thermodynamics; postdoctoral research; post-doctoral research; industrial research; director; John J. Gilman; J. J. (Jack) Gilman (1925-2009); physical metallurgy; Columbia University (New York, New York); engineering; Brown University (Providence, Rhode Island); metallurgy; University of Illinois; Allied Chemical Corporation; decade; research and development; solid state laser; Alexandrite; chromium; activator (phosphor); doped; Chrysoberyl; amorphous metal; metallic glass; transformer core; power transformer; magnetic shielding; Center for Advanced Materials; Lawrence Berkeley Laboratory; Department of Materials Science and Engineering; University of California, Los Angeles; UCLA; office; ashtray; desk; tobacco smoking; smoker; gentleman scientist; order and disorder; short-range order; academic publishing; published; book; scientific literature; scientific paper; article (publishing); industrial management; theory; ball lightning; fellow learned or professional societies; American Physical Society; ASM International (society); American Society for Metals; National Academy of Engineering; abrasion (mechanical); scratch; diamond; glass; plot point (narrative); detective fiction; detective novel; B-movie; idea; costume jewelry; glass jewelry; cubic zirconia (yttria-stabilized zirconia, YSZ); jewelry; simulacrum; simulate; synthetic diamond; soda-lime glass; window glass; hardness; YAG (yttrium aluminum garnet); antiquity; Theophrastus; treatise; On Stones; Pliny the Elder; Naturalis Historia (77 AD); blog; mineral; science; scientific; Germany; German; mineralogist; Friedrich Mohs (1773-1839); Mohs scale of mineral hardness; ordinal scale; Vickers hardness test; pyramid (geometry); pyrimidal; indenter; surface; dimension; Cartesian coordinate system; graph; mineral; Talc, Mg3Si4O10(OH)2; Gypsum, CaSO4·2H2O; Calcite, CaCO3; Fluorite, CaF2; Apatite, Ca5(PO4)3(OH-,Cl-,F-); Orthoclase, KAlSi3O8; Quartz, SiO2; Topaz, Al2SiO4(OH-,F-)2; Corundum, Al2O3; Diamond, C; Inkscape; bond energy; bonding energy; atom; lattice structure of crystals; Erwin Madelung (1881-1972); Madelung constant; calculate; electrostatic; fundamental interaction; force; ionic bond; crystal; lattice energy; kilojoule; kJ; mole (unit); mol; sodium chloride; NaCl; theoretical yield strength; shear strength; shear modulus; experiment; experimental; pascal (unit); MPa; tension (physics); stress (mechanics); dislocation; crystal structure; crystal plane; polycrystal; polycrystalline; fracture; aerospace engineering; aeronautical engineer; Alan Arnold Griffith (1893-1963); glass fiber; notch (engineering); Griffith's criterion; brittleness; brittle; product (mathematics); square root; length; constant (mathematics); energy; superhard material; cutting tool (machining); wear-resistant; coating; cost; oxide; oxidize; temperatures; celsius; °C; efficiency; inefficient; iron; ferrous; alloy; dissolution (chemistry); dissolve; cementite; iron carbide; covalent bond; carbon; atomic number; chemical element; boron; nitrogen; oxygen; ternary compound; transition metal; theory; beta-carbon nitride (β-C3N4); chemical synthesis; synthesize; cubic boron nitride (β-BN); rhenium diboride (ReB2); electronegativity; rhenium; ambient pressure; microindentation; X-ray crystallography; X-ray diffraction analysis; bulk modulus; carbide; boride; open access paper; Physical Review letters; Michael Chandross; Nicolas Argibay; Sandia National Laboratories (Albuquerque, New Mexico); nonlinear regression; fitting parameter; thermodynamics; amorphization; mathematical model; Creative Commons Attribution 4.0 International license; crystallite; grain; grain boundary; nanometer; nm; ductility; soft; grain boundary strengthening; Hall-Petch law; order and disorder (physics); activation energy<; deformation (mechanics; cubic crystal system; body-centered cubic; hexagonal crystal family; hexagonal close packed; face-centered cubic; axiom; assumption<; melting; melt; equation; melting point; enthalpy of fusion; heat of fusion; volume fraction; phase transition; transformation.