Computing Chaos
November 11, 2019
Language has a way of retaining descriptive
words after their actual relation to what was originally described is long absent. One example is using the word
film to describe a
motion picture. Motion pictures were originally displayed by shining a bright
lamp through images on long
reels of
transparent film, and that's why motion pictures were called films. Now, motion pictures are displayed more
efficiently, less
expensively, and in better
definition, though use of
digital technology.
Another example is in
integrated circuit design. When an integrated circuit design is approved for
fabrication, the design is
taped-out. Today, tape-outs take the form of a digital
data file that provides instructions for the preparation of a
photomasks using
electron-beam lithography or another lithographic process. The term, tape-out, comes from the early days of this process in which black
adhesive tape was manually applied to huge transparency sheets for photoreduction to a
die-sized photomask image.(see photograph).

Integrated circuit layout adhesive tape (c. 1965). The large squares are one inch on a side.
I purchased this reel at an electronics store that acted as a conduit for surplus from several General Electric factories and a General Electric research and development facility that fabricated components for the Apollo Program, including the Lunar Excursion Module (LEM).
(Photo by the author).
Tape-out is an important
milestone, since a lot of
money would be wasted if the design contains errors. Today, error checking is a huge task, since integrated circuits are so complex. The
transistor count of today's computer chips is, to borrow a phrase from
astronomer,
Carl Sagan,
billions and billions. The
AMD Epyc Rome microprocessor has 32 billion transistors.
32 billion transistors is many orders of magnitude larger than the 3.1-4.5 million transistors of the
Pentium microprocessors introduced in the
1990s; so, you would think that error checking before tape-out would have been easy. This computer chip included
circuitry for a
hardware floating-point processor, and this enhanced the speed of
spreadsheet calculations. Shortly after the Pentium's introduction, however, a subtle error in the floating point unit gave an incorrect result in about one out of every ten billion calculations.
This error, now known as the
Pentium FDIV bug, was discovered by
Thomas R. Nicely, a
professor at Lynchburg College (now, the
University of Lynchburg (Lynchburg, Virginia), whose
website (
www.trnicely.net/) is an enjoyable destination.[1] Nicely found that for a range of numbers, the Pentium floating point processor computed results wildly outside the supposed 19
significant digits; for example,
(824633702441.0)*(1/824633702441.0) = 0.999999996274709702
Of course, the result of the calculation should be
unity.
Intel, the
manufacturer of the Pentium, tracked the problem to errors in a
lookup table, did a
recall of all affected chips, and took a $475 million
loss in replacement of these chips. I remember doing a check for this error on my own Pentium computer at the time, and the check verified the problem.
While I've done some calculations with
arbitrary-precision arithmetic as implemented by the
GNU Multiple Precision Arithmetic Library, nearly all computation can be done using
floating-point arithmetic, generally following the
IEEE 754 standard. A
32-bit floating point number (single precision, or
float in the
C language) has a
24-bit (16,777,216)
precision, while a
64-bit floating point number (double precision, or
double in C) has a 53-bit (9,007,199,254,740,992) precision.
I ran the following simple C language on my current desktop computer as a check of the floating point implementation:
#include <stdio.h>
#include <stdlib.h>
int main(void)
{
double n;
n=824633702441.0;
printf("\nresult = %.19lf\n",(n*(1/n)));
return 0;
}
The result was
0.9999999999999998890, which was the expected precision.
Computer scientists realized from the time of the first
computer simulations that the precision of calculation was an important factor. The classic example is the 1961 discovery by
American meteorologist,
Edward Norton Lorenz (1917-2008), that a rerun of a simulation using a stored, but less precise,
snapshot of its last state gave a wildly different result.[2] As he wrote in his
paper that summarized this result and established
chaos theory as a
scientific discipline,
"Two states differing by imperceptible amounts may eventually evolve into two considerably different states ... If, then, there is any error whatever... and in any real system such errors seem inevitable - an acceptable prediction of an instantaneous state in the distant future may well be impossible."[2]
The precision of computations has improved in the half
century since Lorenz's discovery. Simulations much less involved than
weather forecasting are now done with reduced fear that their results are far different from reality, especially when a range of simulations are
averaged to
statistically deduce a general
trend. However, a study by
mathematicians and computer scientists from
Tufts University (Medford, Massachusetts),
University College London (UCL, London, UK), and the
University of Amsterdam (Amsterdam, Netherlands) has shown that simulators should not be too
complacent.[3-4] Their recent
open access paper in
Advanced Theory and Simulations shows that the statistical properties of a
chaotic dynamical system called a
generalized Bernoulli map have errors the cannot be mitigated by increasing the precision of the floating point numbers.[3]

Scientific press releases are often accompanied by interesting artwork, such as "The Great Floating Point Wave" depicted here.[4]
This is an adaptation of the famous c.1830 woodblock print entitled, "The Great Wave Off Kanagawa," by Japanese Edo Period artist, Hokusai.
(University College London image by P V Coveney, H S Martin & Charu G, also available here.)
Says
Peter Coveney, a professor at University College London,
director of the
UCL Centre for Computational Science, and an
author of the study,
"Our work shows that the behavior of the chaotic dynamical systems is richer than any digital computer can capture. Chaos is more commonplace than many people may realize and even for very simple chaotic systems, numbers used by digital computers can lead to errors that are not obvious but can have a big impact. Ultimately, computers can't simulate everything."[4]
The generalized Bernoulli map has a single free
parameter, β, and the exact properties of the map are known. It's used to represent systems that are chaotic in time such as
physical,
biological, and
chemical processes, examples being
chemical reactions and
climate change.[4] In comparing the known values of the Bernoulli map with its simulations, the research team found that some values of β give somewhat correct results (within 15%) while others are totally incorrect.[4]
Odd integer values of β give more accurate results, but the relative errors are two
orders of magnitude larger than those that can be attributed to
roundoff error.[3]
One source of error might be the fact that the
range of floating-point numbers from
positive to negative infinity are not
distributed uniformly.[4] As
Bruce Boghosian, a professor at Tufts University and first author of the paper, explains,
"The four billion single-precision floating-point numbers that digital computers use are spread unevenly, so there are as many such numbers between 0.125 and 0.25, as there are between 0.25 and 0.5, as there are between 0.5 and 1.0. It is amazing that they are able to simulate real-world chaotic events as well as they do. But even so, we are now aware that this simplification does not accurately represent the complexity of chaotic dynamical systems, and this is a problem for such simulations on all current and future digital computers."[4]
Although one might think that increasing computational precision is all that's needed to prevent error, the research team says that, for this problem, going from single to double precision doesn't help that much.[3-4] The problem is in the
discrete nature of the floating-point numbers when trying to simulate such sensitive chaotic dynamical systems.[3] The
mantissa and
exponent fields of floating-point numbers are of finite length when encoded in any
radix. The authors write that this example should act as a warning about the uncritical application of
numerical methods in studies of such processes as
turbulence and
molecular dynamics.[3]
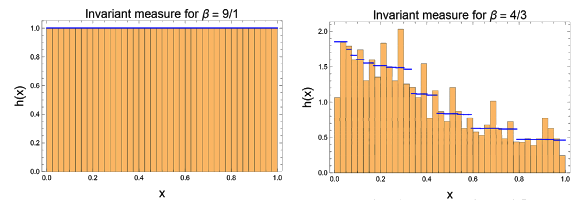
Histograms of errors in generalized Bernoulli map computations. The exact values (blue) are compared with the simulated averages obtained for an infinite length of time and an infinite ensemble size. Odd integer values of β give good agreement, while non-integer β values do not fare as well. (Portion of fig. 4 of ref. 3, distributed under a Creative Commons Attribution License).[3]
References:
- Thomas R. Nicely, Archived text of Pentium FDIV bug announcement email, October 30, 1994.
- Edward N. Lorenz, "Deterministic Nonperiodic Flow," Journal of the Atmospheric Sciences, vol. 20, no. 2 (1963), pp. 130-141, doi:10.1175/1520-0469(1963)020<0130:DNF>2.0.CO;2 (PDF File).
- Bruce M. Boghosian, Peter V. Coveney, and Hongyan Wang, "A New Pathology in the Simulation of Chaotic Dynamical Systems on Digital Computers," Adv. Theory Simul., Article no. 1900125, September 23, 2019, https://doi.org/10.1002/adts.201900125 (8 pages). This is an open access article with a PDF file here
- Numbers limit how accurately digital computers model chaos, University College London Press Release, September 23, 2019.
Linked Keywords: Language; word; film; motion picture; lamp; reel; transparency; transparent; efficiency; efficient; expense; expensive; high-definition video; digital; technology; integrated circuit; design; semiconductor device fabrication; tape-out; taped-out; data; computer file; photomask; electron-beam lithography; adhesive tape; die (integrated circuit); integrated circuit layout; ssquare; inch; reel; electronics; retail store; conduit; surplus store; General Electric; factory; research and development; electronic component; Apollo Program; Lunar Excursion Module (LEM); milestone (project management); money; transistor count; astronomer; Carl Sagan; billions and billions; Advanced Micro Devices; AMD; Epyc Rome; microprocessor; Pentium microprocessor; 1990s; hardware floating-point processor; spreadsheet; calculation; Pentium FDIV bug; Thomas R. Nicely; professor; University of Lynchburg (Lynchburg, Virginia); website; www.trnicely.net/; significant figures; significant digits; unity; Intel; manufacturing; manufacturer; lookup table; product recall; loss (income statement); arbitrary-precision arithmetic; GNU Multiple Precision Arithmetic Library; floating-point arithmetic; IEEE 754 standard; single-precision floating-point format; 32-bit floating point number; C (programming language); 24-bit; significand; precision; double-precision floating-point format; 64-bit floating point number; computer scientist; computer simulation; United States; American; meteorology; meteorologist; Edward Norton Lorenz (1917-2008); snapshot (computer storage); scientific literature; paper; chaos theory; branches of science; scientific discipline; state (computer science); program state; century; weather forecasting; average; statistics; statistical; deductive reasoning; deduce; trend estimation; mathematician; Tufts University (Medford, Massachusetts); University College London (UCL, London, UK); University of Amsterdam (Amsterdam, Netherlands); complacency; complacent; open access journal; open access paper; Advanced Theory and Simulations; chaos theory; chaotic; dynamical system; generalized Bernoulli map; science; scientific; press release; art; artwork; adaptation (arts); woodblock printing in Japan; woodblock print; The Great Wave Off Kanagawa; Japan; Japanese; Edo Period; artist; Hokusai; Peter Coveney; director; UCL Centre for Computational Science; author; parameter; physics; physical; biology; biological; chemistry; chemical; chemical reaction; climate change; parity (mathematics); odd integer; orders of magnitude; roundoff error; interval (mathematics); range; extended real number line; positive to negative infinity; discrete uniform distribution; distributed uniformly; Bruce Boghosian; discrete mathematics; mantissa (logarithm); exponentiation; exponent; radix; numerical analysis; numerical method; turbulence; molecular dynamics; histogram; computation; simulation; simulate; average; infinity; infinite; statistical ensemble (mathematical physics); Creative Commons Attribution License.