Christmas 2019
December 23, 2019
Tikalon is on a year-end
holiday. Our next article will be posted on Monday, January 6, 2020. Here are a few things to think about on that
long drive to grandma's house.
Christmas is about
nativity, so
birthdays are the theme of this article. It's interesting to note that
physicist and
mathematician,
Isaac Newton, was born on
Christmas Day, December 25, 1642.
Humans have always been oppressed by
conventions adopted from earlier times. An example of this is the number of
days in a
week. One of my
childhood speculations involved how different our lives would be if there were six, instead of seven, days in a week. Would our weeks be structured as four
school and
working days, followed by two
leisure days, thereby giving us weekends expanded by 4.7%? There's the alternative dark
scenario in which we have five working days and just one leisure day in that six day week. That might be the topic of a
dystopian novel.
Leap years cause a problem for the 0.07% of the
population born on
leap year day, February 29. In principle, they have a
birthday every four years, which would be a
tragedy for a
child seeing everyone except him/her get an
annual party and associated
gifts. This problem is solved by using a different
enumeration of
date. It's either the day after
February 28, or the day before
March 1.

Saint Nicholas of Myra (March 15, 270 - December 6, 343) anonymously donating dowry money for a penniless man's three daughters by pushing gold coins through a window.
Santa Claus is associated with Saint Nicholas in the Dutch tradition of Sinterklaas; so, Santa's birthday would be March 15, which is also the Ides of March.
(Detail from a 1437 tempera on wood painting by Fra Angelico in the Vatican collection, via Wikimedia Commons image. Click for larger image.)
Birthdays are quite
uniformly distributed, although there are some factors that lead to slightly more birthdays one
gestation period (nine months) after significant events such as
New Year's Day, or the
northeast blackout of 1965. Assuming uniformity and ignoring leap years, two people will share the same birthday with the
probability, 1/365, or about 0.27%. That's because the second person has just one chance in 365 of having the same birthday as the first.
When we consider a large number of people, such as
students in a
classroom, we can explore another aspect of birthdays called the
birthday problem. I was introduced to this problem in
high school during a series of
mathematics seminars hosted by
Colgate University (Hamilton, New York). In this case, we don't ask whether someone has a birthday on a specific day, but whether any two of those assembled share a birthday. If
N is the number of people in addition to the first, the probability
P(N) of any two having the same birthday is given as
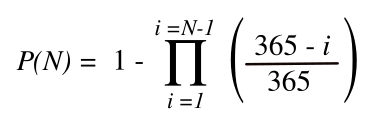
Of course, having 365 people will give a probability of one by the
pigeonhole principle. The surprising thing is that you need just 23 people to give a 50% probability. A
graph of probabilities as a
function of the number of people in a group is given below.
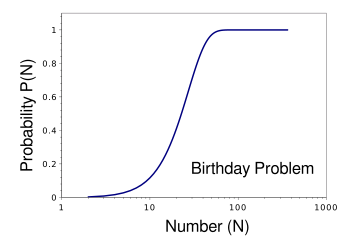
Graph of birthday problem probabilities. In this graph, N is the total number of people, not those in addition to the first person, as expressed in the equation.
Only 23 people are needed to give a 50.7% probability, or better than a 50:50 chance.
(Graphed using Gnumeric. Click for larger image.)
The birthday problem also has application to
cryptography.
Cryptographic hash functions are used for storing
passwords in
coded form and confirming that a
document has not been altered (e.g. using a hash in a
digital signature). It's difficult to generate a document having the same hash value as another, but it's much easier to generate two documents having the same hash value, an attribute called a
collision. A so-called
birthday attack produces a good chance of a collision after only 2
N/2 codes, while the complete hash space has 2
N codes. A 64-bit hash has 1.8 x 10
19 possible values, but only 5 billion attempts are needed to generate a collision in a 64-bit hash with 50% probability.
Linked Keywords: Tikalon; holiday; Over the River and Through the Wood; long drive to grandma's house; Christmas; birth; nativity; birthday; physicist; mathematician; Isaac Newton; Christmas Day; human; convention (norm); day; week; childhood; sSpeculative reason; speculation; school; wage labor; work (labor); leisure; scenario; dystopia; dystopian; novel; leap year; population; born; leap year day, February 29; tragedy; child; annual; party; gift; enumeration; calendar date; February 28; March 1; Saint Nicholas of Myra (March 15, 270 - December 6, 343); anonymity; anonymously; donation; donate; dowry money; poverty; penniless; daughter; gold coin; window; Santa Claus; Dutch people; traditional story; tradition; Sinterklaas; Ides of March; tempera; wood; painting; Fra Angelico; Vatican Museums; Vatican collection; Wikimedia Commons; discrete uniform distribution; uniformly distributed; gestation period; New Year's Day; northeast blackout of 1965; probability; student; classroom; birthday problem; high school; mathematics; seminar; Colgate University (Hamilton, New York); pigeonhole principle; Cartesian coordinate system; graph; function (mathematics); equation; Gnumeric; cryptography; cryptographic hash function; password; coded form; document; digital signature; collision (computer science); birthday attack.