Bus Stop Simulation
November 5, 2018
Humans progressed from
itinerant hunter-gatherers to
farmers living in a single place. Now, it seems that we've reverted to our hunter-gatherer roots, as we hunt for new
jobs in different places, travel on
business, hunting for new
customers, and gathering
doughnuts and
coffee on our long
morning commutes.
Transportation has become an integral part of our modern
civilization, and
automobiles are a necessity in
suburban life. In my suburb of
Northern New Jersey, every
family member of
driving age has an automobile.
As
scientists decry the build-up of
atmospheric carbon dioxide caused by all this
burning of
fossil fuel, it also inspires their
research into
clean energy alternatives. Long before we worried about
greenhouse gases, there was some interesting
mathematics inspired by a
taxicab. In 1919, the eminent
British mathematician and
number theorist,
G.H. Hardy, was visiting his
colleague,
Srinivasa Ramanujan, at a
hospital. I wrote about this encounter in an
earlier article (Special Numbers, September 21, 2011). As Hardy wrote,
I remember once going to see him when he was ill at Putney. I had ridden in taxi cab number 1729 and remarked that the number seemed to me rather a dull one, and that I hoped it was not an unfavorable omen. "No," he replied, "it is a very interesting number; it is the smallest number expressible as the sum of two cubes in two different ways."[1]
This
Hardy–Ramanujan number, known as the second "
taxicab number" (Ta(2)), can be expressed as 1
3 + 12
3 = 1729, and 9
3 + 10
3 = 1729. The first taxicab number, Ta(1) = 1, is a
trivial case, since 1
3 + 1
3 = 2. At this time, there are six known taxicab numbers, given as
sequence A011541 in the
On-Line Encyclopedia of Integer Sequences: 2, 1729, 87539319, 6963472309248, 48988659276962496, and 24153319581254312065344.

Taxicab no. 1729 of the Hardy-Ramanujan Cab Company. (Source image via Wikimedia Commons.)
Today, taxicabs are being replaced by
ride services such as
Uber, but people still drive their personal automobiles to work. In some cases,
employees living near each other and working for the same
company will form a
carpool in which the driving duties are cycled among the participants. In a five person carpool, this would require each participant to drive on a particular
weekday. This is an
equitable arrangement when all these employees travel together each day, but there are invariably
business trips,
vacations,
illness, and other circumstances, that prevent certain of them from participating on some days.
This leads to the problem of who will drive on those days when the designated
driver is away; and, how would this absent driver repay his colleagues for his lack of service on those days. Perhaps motivated by the
US energy crisis of 1979, a
mathematician and a computer scientist from
IBM published a paper on carpool
scheduling in 1983. I wrote about their
fair carpool
algorithm in an
earlier article (Fair Carpooling Algorithm, April 21, 2011).
The fair carpooling algorithm involves a
balance sheet among the participants in which driving is considered to have a
fixed cost. To keep
accounting in the
integer realm, this cost
U is a number that's the
least common multiple of the number of carpool participants. In a carpool with 4 participants,
U would be 12, a number that's divisible by 1, 2, 3, and 4. If a particular trip has
k participants, the participants who are not drivers need to "
pay" the driver
U/k units, and everyone's personal account is updated on the balance sheet. The balance sheet will always indicate which participant has the smallest amount in his/her account, and that person should be the next driver.[2]
Since
commuting to work affects the lives of many people worldwide, carpooling
optimization continues to excite a scientist's imagination. To date, the IBM paper has nearly 20,000
citations. While most carpools consist of employees living in close proximity who travel to the same workplace, the carpool scheme can extend to participants who live somewhat distant from each other and work at different places in reasonable proximity. The
Internet has facilitated formation of these carpools. A team of
Chinese researchers has examined carpool optimization for commuting in
Guangzhou, China, and they've presented their model in an
open access paper in
PLoS.[3] They found that it takes more than a single algorithm for efficient carpooling in an extended carpooling scheme.
Public transportation via
buses,
light rail, and
subway is usually the most efficient mode for commuting, so
governments are doing things to encourage ridership. While
subsidized fares are a good idea, it's also important to make the ride as pleasant as possible. Clean,
air conditioned vehicles are important, but also important is telling riders when their vehicle will arrive. Today's
GPS and
cellular networks have allowed the riders themselves to provide information as to when their bus has arrived and relay that information to project the arrival time for other riders down the line.[4]

A New York City Subway token. Subway tokens were replaced by the more manageable Metrocard on April 14, 2003.
Every time I see one of these, I think of Y Combinator.
(Wikimedia Commons image by Jessamyn West.)
When we were being taught
derivatives in
high school calculus, one of my fellow
students posed a question that seemed like a
rate problem. His question was whether he would be at his
bus stop on time if the bus was first visible to him when he was at a certain distance from the bus stop. Since we lived in a
city, the problem was that
buildings will interfere with the
line-of-sight, so the bus was only
visible when he was quite near the bus stop. The problem is best explained by the diagram, below.
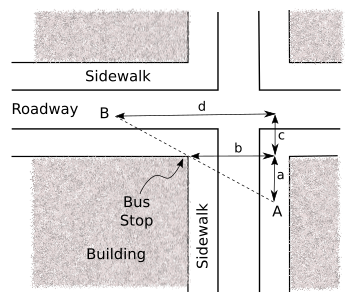
The bus stop problem.
The student is at A, and the bus is at B. The bus stop is at the corner of the building, and it's assumed that there is no traffic and no crossing signal to delay travel across the street.
The student needs to walk the distance a + b to reach the bus stop, and the bus travels the distance d - b to reach the bus stop.
We want to know the distance at which you can see the bus and travel to the bus stop before the bus gets there.
(Click for larger image.)
Since a
high school student's hormone-addled
brain needs maximal
teaching, we continued with derivatives and never solved the problem. The problem always stayed on my mind, so I decided to solve it. Simple
geometry and a
spreadsheet was all that was required. Using the
property of similar triangles, we find that
d/(c+a) = b/a
Since
b and
c are
constants with values from my own experience of
b = 80 ft. and
c = 35 ft., we can use
estimated travel rates for the student (
ra = 3
ft/sec) and the bus (
rb = 20 ft/sec) to
calculate the travel times to the bus stop for a range of
a values; viz.,
ta = (a+b)/ra
tb = (d-b)/rb
The following
graph illustrates the results of the spreadsheet calculation using
Gnumeric.
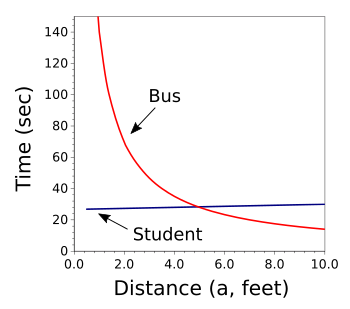
Solution of the bus stop problem as the time for the student and bus to reach the bus stop as a function of the student's distance a to the intersection.
If the student sees his bus when he's more than five feet from the intersection, there's no hope that he will reach the bus stop on time.
(Graphed using Gnumeric.)
As can be deduced from the graph, the student will miss his bus if he sees it when he's more than five
feet from the
intersection. Just after our high school
graduation, the
The Hollies released the 1966 recording,
Bus Stop.[5]
References:
- Quotations of Godfrey Harold Hardy on Wikiquote.
- Ronald Fagin and John H. Williams, "A Fair Carpool Scheduling Algorithm," IBM Journal of Research and Development, vol. 27, no 2 (March 1983), pp. 133-139, DOI: 10.1147/rd.272.0133. A PDF file of this paper is available here and here.
- Jizhe Xia, Kevin M. Curtin, Weihong Li, and Yonglong Zhao, "A New Model for a Carpool Matching Service," PLOS, vol. 10, no. 6 (June 30, 2015), article no. e0129257, https://doi.org/10.1371/journal.pone.0129257. This is an open access article with a PDF file available here.
- Ed Blazina, "'GPS for transit': More real-time transit information available in Pittsburgh," Pittsburgh Post-Gazette, Aug 27, 2018.
- Bus Stop- The Hollies - 1966, YouTube Video by 74sodapop.
Linked Keywords: Human; itinerant; hunter-gatherer; agriculture; farmer; employment; job; business; customer; doughnut; coffee; morning; commuting; commute; transportation; civilization; automobile; suburb; suburban; Northern New Jersey; family member; driving age; scientist; atmospheric carbon dioxide; combustion; burning; fossil fuel; research; sustainable energy; clean energy; greenhouse gas; mathematics; taxicab; Great Britain; British; mathematician; number theory; number theorist; G.H. Hardy; colleague; Srinivasa Ramanujan; hospital; disease; ill; Royal Hospital for Neuro-disability; Putney; number; omen; cube (algebra); Hardy–Ramanujan number; taxicab number; triviality (mathematics); trivial case; sequence A011541; On-Line Encyclopedia of Integer Sequences; Wikimedia Commons; peer-to-peer ridesharing; ride service; Uber; employee; company; carpool; weekday; equitable; business trip; vacation; illness; driver; US energy crisis of 1979; IBM; schedule; scheduling; equitable; fair; algorithm; balance sheet; fixed cost; accounting; integer realm; least common multiple; wage; pay; commuting; optimization; citation; Internet; Chinese; researchers; Guangzhou, China; open access paper; PLOS; public transportation; bus; light rail; rapid transit; subway; government; subsidy; subsidize; fare; air conditioning; air conditioned; vehicle; Global Positioning System; GPS; cellular network; New York City Subway; token; Metrocard; Y Combinator; Jessamyn West (librarian); derivative; high school; calculus; student; rate (mathematics); bus stop; city; building; sightline; line-of-sight; visibility (geometry); visible; traffic; traffic light; crossing signal; street; hormone; brain; education; teaching; geometry; spreadsheet; property of similar triangles; constant (mathematics); estimation; estimated; foot per second; ft/sec; calculation; calculate; Cartesian coordinate system; graph; Gnumeric; time; function (mathematics); intersection (road); foot (length); graduation; The Hollies; Bus Stop (song).