| Tikalon Blog is now in archive mode.
An easily printed and saved version of this article, and a link
to a directory of all articles, can be found below: |
|
This article |
| Directory of all articles |
Claude Shannon's Long Division
January 15, 2018
2016 was the
centennial of the
birth of
Claude Shannon (1916-2001), the founder of
information theory. I wrote an article about Shannon in that year (
Claude Shannon, April 28, 2016). For
Christmas, 2017, I received from my
son the well written
biography of Shannon by
Jimmy Soni and
Rob Goodman.[1] The book is intended for
general audiences, so it contains a lot of interesting, but
ancillary, information that doesn't relate directly to Shannon, which is my only complaint. My son knew exactly what I wanted for Christmas, since he's always careful to ask me beforehand. For Christmas, 2016, he gave me a
Raspberry Pi 3, a
single board computer that runs the
Linux operating system.
Claude Shannon demonstrating a maze-solving mouse, called Theseus, in 1950.[2]
Electronic computing devices were still primitive in 1950, so the necessary computation and memory operations for Theseus were done using electromechanical relays.
The mouse was named Theseus in reference to Θησευς, who escaped the Minotaur's Labyrinth.
(Still image from a YouTube video by BinarycoreMedia, April 30, 2013, modified for artistic effect.)[2]
Shannon, like many other
young scientists and
engineers,
tinkered with
technology during his
childhood. He built
mechanical and
electrical devices, including a
radio transmitter and
receiver. Since he enjoyed both
electronics and
mathematics, Shannon
graduated from the
University of Michigan in 1936 with
degrees in both
electrical engineering and math. As a
graduate student at
MIT, he wrote a
Master's thesis entitled,
A Symbolic Analysis of Relay and Switching Circuits. This thesis was on the use of
Boolean algebra for efficient
switching of telephone circuits.
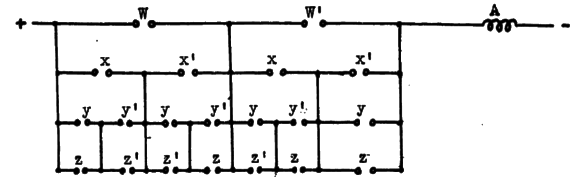
Figure 30 from Claude Shannon's 1940 Master's thesis. (Via MIT Library.)[3]
After earning his
Ph.D., Shannon became a
National Research Fellow at the
Institute for Advanced Study (Princeton, New Jersey). He then joined
Bell Labs to work on
military projects, including
cryptography, during
World War II. In his cryptographic work, Shannon proved that properly constructed
one-time pads were unbreakable.
At Bell Labs, Shannon published his most famous
paper, "
A Mathematical Theory of Communication," in 1948 in two parts in the
Bell System Technical Journal.[4-5] This paper was the foundation of information theory. In it, Shannon defined the concept of
information entropy.
Shannon joined MIT's faculty and its
Research Laboratory of Electronics in 1956. He was a faculty member at MIT until 1978. Shannon developed
Alzheimer's disease, and he died on February 24, 2001. Among his many honors, Shannon received the 1966
National Medal of Science, presented by
President Lyndon B. Johnson. Through it all, he was
modest about his accomplishments, and he worried that they were being "oversold."[6]
Early in their biography of Shannon, on page 19, Soni and Goodman write about Shannon's first
publication, accomplished at age 17.[1] This was the solution to a problem in
long division posed a few months earlier in
The American Mathematical Monthly by R.M. Sutton of
Haverford College, Pennsylvania.[7-8] This wasn't a standard long division; rather, it was a long division encoded by a
cryptographic substitution of
alphabet letters for
numbers, as shown below.
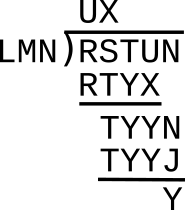
As can be
surmised, all the numbers from zero through nine have been substituted by some letter from the set, J,L,M,N,R,S,T,U,X, and Y. Not only was the solution difficult, but so was Sutton's finding a simple long division that contained all the
digits. In this age of
spreadsheets and
calculators, it's rare when a person does a long division by hand. While long division by hand seems
inelegant, a longer step from elegance was my decision to solve this problem by a
brute force computer program.
A brute force attack, also called a proof by exhaustion and a proof by cases, involves checking each possible case. One famous example of a brute force attack is the
computer-assisted proof of the
Four-Color Conjecture that you need only four colors to color a
map such that no adjacent regions have the same color. This conjecture was not easy to prove
analytically, but
Kenneth Appel and
Wolfgang Haken used a computer to analyze every conceivable map to prove the conjecture true in 1976.[9-10] They analyzed all 1,936 cases of the problem using available computers of that time, an
IBM 360-75, an
IBM 370-158, and an
IBM 370-168.[10]
The Sutton long division has ten
variables, each of which has ten possible values. This long division requires the four
equations shown below to be simultaneously true. This leads to 10
10 (ten billion) cases involving four calculations each. The
C language program that I wrote is a trivial assemblage of ten
nested loops (
source code,
here, shannon.c).
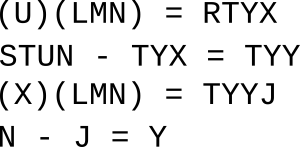
This is not the type of program you should ever admit writing, and you can wear out your
curly-brackets keys. However, all these nested loops executed on my
Ubuntu 16.04.3 LTS 64-bit four core Intel i3-4160 3.60GHz
desktop computer with 8
gigabytes of
RAM in just 17.171509 seconds, obtaining the first (and only) solution in just 2.786426 seconds. The solution is J = 1, L = 6, M = 0, N = 3, R = 5, S = 8, T = 4, U = 9, X = 7, and Y = 2.
My son, who's an actual
computer scientist, produced an improved version of the program, with source code
here, shannon2.c. His program obtains the solution in 0.605299 seconds, nearly five times faster, on my desktop computer.
References:
- Jimmy Soni and Rob Goodman , "A Mind at Play: How Claude Shannon Invented the Information Age," Simon & Schuster, July 18, 2017, ISBN-13: 978-1476766683, 384 pp. (via Amazon).
- Claude Shannon demonstrates machine learning, YouTube Video by Sean Palmer, May 17, 2014. In this video, Shannon describes himself as a mathematician.
- Claude Elwood Shannon, "A symbolic analysis of relay and switching circuits," Master's Thesis, MIT Library, 1940 (PDF File).
- Claude E. Shannon, "A Mathematical Theory of Communication", Bell System Technical Journal, vol. 27, no. 3 (July, 1948), pp. 379-423.
- Claude E. Shannon, "A Mathematical Theory of Communication", Bell System Technical Journal, vol. 27, no. 4 (October, 1948), pp. 623-656.
- G. Pascal Zachary, "Celebrating Claude Shannon," IEEE Spectrum April, 2016, p. 8.
- R. M. Sutton, Problem E58, The American Mathematical Monthly, vol. 40, no. 8 (October, 1933), p. 491f., DOI: 10.2307/2302079.
- C. E. Shannon, Problem E58 Solution, The American Mathematical Monthly, vol. 41, no. 3 (March, 1934), p. 191f., DOI: 10.2307/2302271.
- K. Appel and W. Haken, "Every planar map is four colorable. Part I: Discharging,"Illinois Journal of Mathematics, vol. 21, no. 3 (1977), pp. 429-490. A PDF file (4817 KB) can be found here.
- K. Appel, W. Haken, and J. Koch, "Every Planar Map is Four Colorable. II. Reducibility", Illinois Journal of Mathematics, vol. 21 no. 3 (1977), pp. 491-567. A PDF file (3811 KB) can be found here.
Linked Keywords: Centennial; birth; Claude Shannon (1916-2001); information theory; Christmas; son; biography; Jimmy Soni; Rob Goodman; general audiences; ancillary; Raspberry Pi 3; single board computer; Linux operating system; maze; mouse; computer; electronic computing devices; computation; computer memory; electromechanics; electromechanical; relay; Theseus; Θησευς; Minotaur; Labyrinth; YouTube video; BinarycoreMedia; youth; young; scientist; engineer; tinker; tinkered; technology; childhood; mechanical; electricity; electrical; radio transmitter; radio receiver; electronics; mathematics; graduation; graduate; University of Michigan; Bachelor of Science; degree; electrical engineering; postgraduate education; graduate student; Massachusetts Institute of Technology; MIT; Master's thesis; A Symbolic Analysis of Relay and Switching Circuits; Boolean algebra; telephone exchange; switching of telephone circuits; MIT Library; Doctor of Philosophy; Ph.D.; National Research Council United States; National Research Fellow; Institute for Advanced Study (Princeton, New Jersey); Bell Labs; military; cryptography; World War II; one-time pad; academic publishing; paper; A Mathematical Theory of Communication; Bell System Technical Journal; information entropy; Research Laboratory of Electronics at MIT; Alzheimer's disease; National Medal of Science; President of the United States; Lyndon B. Johnson; modesty; modest; publication; long division; The American Mathematical Monthly; Haverford College, Pennsylvania; substitution cipher; cryptographic substitution; alphabet; letter; natural number; surmise; numerical digit; spreadsheet; calculator; elegance; inelegant; proof by exhaustion; brute force; computer program; computer-assisted proof; four color theorem; Four-Color Conjecture; map; mathematical analysis; analytical; Kenneth Appel; Wolfgang Haken; IBM System/360 Model 75; IBM System/370 Model 158; IBM System/370 Model 168; variable; equation; C programming language; control flow; nested loops; source code; shannon.c; curly-bracket; computer keyboard; Ubuntu operating system 16.04.3 LTS; 64-bit; multi-core processor; four core; Intel i3-4160; desktop computer; gigabyte; random-access memory; RAM; computer scientist; Jimmy Soni and Rob Goodman , "A Mind at Play: How Claude Shannon Invented the Information Age," Simon & Schuster, July 18, 2017, ISBN-13: 978-1476766683, 384 pp.