| Tikalon Blog is now in archive mode.
An easily printed and saved version of this article, and a link
to a directory of all articles, can be found below: |
|
This article |
| Directory of all articles |
Random Triangles
January 26, 2017
The
triangle is the simplest
polygon, and triangles are
technologically very useful. Many
computer-generated images are
built from triangles, and the
finite element method decomposes a surface into triangular elements for
analysis of such diverse properties as
thermal conduction and
mechanical stress.
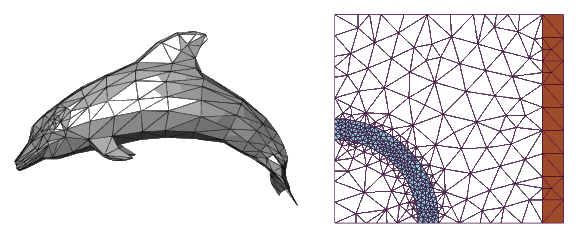
A dolphin image constructed from a triangular mesh, along with a finite element mesh for analysis of the magnetic field in a cylindrically shaped magnetic shield, shaded blue. The red element is a current-carrying wire that generates a test field. (Left, a Wikimedia Commons image by Chrschn; right, a Wikimedia Commons image by Zureks.)
Triangles were an early object of
mathematical study, as the
Pythagorean theorem demonstrates. Although named for the
Greek mathematician and
philosopher,
Pythagoras (c. 570 - c. 495 BC), this theorem may be more ancient by a thousand years. Many
proofs of the Pythagorean theorem exist (
US president James Garfield (1831-1881) gave a novel proof in 1876), a consequence of the ease of working with
right triangles. That's why I was impressed as a
high school student to learn of
Heron's formula for calculating the
area of an arbitrary triangle from the length of its sides.
Hero of Alexandria (c. 10 - 70 AD), more properly, Heron, was both a
mathematician and an early example of an
engineer, having invented quite a few devices. His
steam engine, known as an
Aeolipile, was published in his book,
Pneumatica. This steam engine, although primitive, predates
James Watt by seventeen centuries.
Hero of Alexandria
The proper transliteration of Hero's name from the Greek would be Heron, but he's known as Hero.
(Illustration from the Codex of San Gregorio de Nizance, a ninth century Greek manuscript, via Wikimedia Commons.)
Hero's simple formula for calculating the area
A of an arbitrary triangle from the length of its sides appears in his Metrica (c. 60 AD). Using
a,
b, and
c as the length of the sides, the formula is as follows:
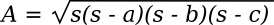
Where the
parameter, s, known as the
semiperimeter, is half the
perimeter; viz.,
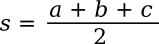
If you want to eliminate the semiperimeter from the formula, the formula can be written in terms of the sides, only, as
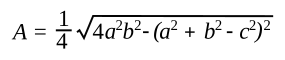
It's easy to verify this using a
3-4-5 right triangle, which will have an area of (1/2)(base)(height) = (1/2)(4)(3) = 6; viz,
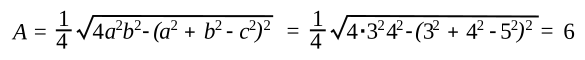Eugen J. Ionascu of the
Department of Mathematics,
Columbus State University (Columbus, Georgia), has recently
published his solution of the interesting problem of how often a fixed
point will be interior to a
random triangle when these are constrained to be drawn inside a variety of
planar regions such as
circles and regular polygons.[1] While the
equations are dense for most of these planar regions, there's a simple case of triangles drawn inside a
unit square in which
numerical estimates are given for certain points. I became interested in this problem as a means to practice my
computer simulation skills.
The primary problem of such a simulation is the method of determining whether the point is inside or outside of the random triangle. An
intuitive method is to draw
vectors from the point to each
vertex of the triangle and sum the
angles between them. If these add to 360°, then the point is inside the triangle. This method is
computationally intensive, so it's not ideal for a simulation.
Another method is to define the location of the point in terms of vectors drawn between two of the vertices using what's called a
barycentric coordinate system (see figure). A moment's reflection will reveal that defining the location of the point as a
linear combination of these two vectors gives an easy way to determine whether or not the point is interior to the triangle. In reference to the figure, this will involve limits on the parameters,
u and
v and their sum.[2]
The location of a point in the interior of a triangle referenced as a linear combination of vectors between vertices. This barycentric coordinate system is nicely explicated in ref. 2.[2]
(Drawn using Inkscape.)
While the required
algorithm to determine a point's location wouldn't be that hard to write, as usual there's someone on the
Internet who's done the necessary
coding for us.[2] That made my simulation program (
source code here) that much easier to write. I first verified the program using an example of a point at (1/3,1/3) presented by Ionascu that gives a
probability of (23/162) + (7ln(2)/243) ≈ 0.161942, and then
conjectured that a point a (1/2,1/2) would have a higher probability than this point, and both would have a higher probability than one at (1/4,1/4).
The results of my simulation appear in the table and figure below.
| | Point x and y | Probability |
| | 0.025 | 0.00065 |
| | 0.04 | 0.00174 |
| | 0.075 | 0.00662 |
| | 0.15 | 0.03038 |
| | 0.25 | 0.09264 |
| | 0.333... | 0.16194 |
| | 0.4 | 0.21360 |
| | 0.5 | 0.25000 |
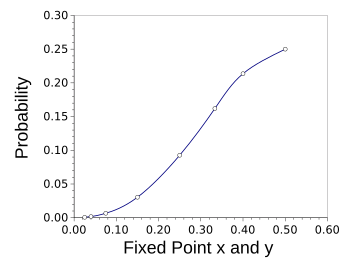
The probability that fixed points of the same x and y values will be in the interior of a random triangle drawn in a unit square.
Interestingly, a point placed in the center has a 25% probability of being inside a random triangle.
(Graphed using Gnumeric.)
When we allow the point to be placed anywhere on the square, the calculated probability is 0.07639. A
histogram of the simulated values for this condition is shown below.
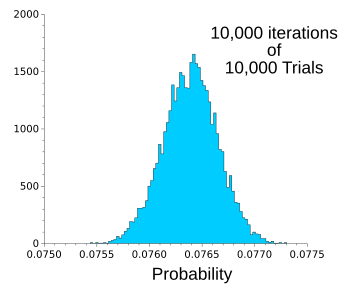
Histogram of simulated values of the probability when the point is placed at random locations on the unit square.
The mean probability is 7.64%.
(Graphed using Gnumeric.)
![]()
References:
- Eugen J. Ionascu, "Random triangles in planar regions containing a fixed point," arXiv, December 15, 2016.
- Barycentric coordinate system, Totologic Blog.
Permanent Link to this article
Linked Keywords: Triangle; polygon; technology; technological; computer-generated images; triangle mesh; finite element method; analysis; thermal conductivity; thermal conduction; mechanical stress; dolphin; magnetic field; cylinder; cylindrical; magnetic shield; electric current; wire; Wikimedia Commons; mathematical; Pythagorean theorem; Ancient Greece; Greek; mathematician; philosopher; Pythagoras (c. 570 - c. 495 BC); proof; US president; James Garfield (1831-1881); right triangle; high school student; Heron's formula; area; Hero of Alexandria (c. 10 - 70 AD); engineer; steam engine; Aeolipile; James Watt; transliteration; Greek language; ninth century; manuscript; parameter; semiperimeter; perimeter; special right triangle; 3-4-5 right triangle; Eugen J. Ionascu; Department of Mathematics; Columbus State University (Columbus, Georgia); scientific literature; publish; point; random; plane; planar; circle; equation; unit square; number; numerical; approximation; estimate; computer simulation; intuition; intuitive; vector; vertex; angle; computation; barycentric coordinate system; linear combination; Inkscape; algorithm; Internet; computer programming; coding; source code; triangle interior point.c; probability; conjecture; probability; Gnumeric; histogram; arithmetic mean.