Noise Thermometry and the Boltzmann Constant
September 11, 2017
How do we measure
temperature? In my
laboratory, I used a
panoply of
temperature-measuring instruments, each designed to accurately cover a certain temperature range. For the highest temperatures, there were
platinum-rhodium thermocouples that gave a
voltage dependent on temperature up to 1600 °C. Near
room temperature there were
platinum resistance thermometers based on the temperature-variable
resistance of platinum.
Most people have used the expressions, "red hot" and "white hot," without knowing their origin. A body will emit temperature-dependent
radiation,
infrared near room temperature, becoming
visible at higher temperatures. All this is quantified by
Planck's law that describes the
spectral density of
electromagnetic radiation that's emitted by a
black body in
thermal equilibrium at temperature T. As temperature is increased, more energy spills into visible
wavelengths (see figure).
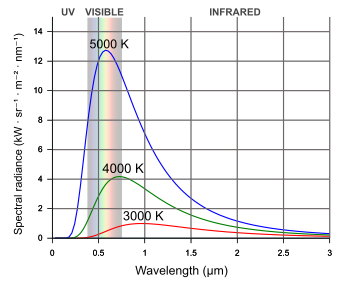
Black body curves.
(Modified Wikimedia Commons image by Darth Kule.
One interesting
thermometer I used to measure very high temperature was a
hot wire pyrometer that used the Planck radiation law as its working principle. This pyrometer was essentially a
telescope through which you could view your
crucible, and in the same
eyepiece you also saw a
metal wire internal to the pyrometer. The procedure was to increase
current through the wire until it glowed with the same
color as your crucible, read the current, and then convert to temperature. Since what was being viewed, and the metal wire, were not strictly black bodies, there were necessary corrections based on material
emissivity. All this didn't give you much confidence in your final temperature reading.
The problem with all thermometers is that they needed to be
calibrated, and that's where the fundamental definition of temperature, the
thermodynamic temperature, enters the discussion. The
gas thermometer, one manifestation of a
thermodynamic thermometer, makes use of
Charles' Law, which states that the
volume occupied by an
ideal gas at a fixed
pressure will be
proportional to the
absolute temperature.

Principle of a gas thermometer.
While atmospheric pressure is a convenient working pressure, it's not quite constant. Helium, however, functions as a good ideal gas, since it's inert, monoatomic, and it remains a gas to very low temperatures.
(Created using Inkscape.
The
physical properties of nearly everything are highly temperature-dependent, so you can build a thermometer
in many ways. Some principal methods are listed on the
website of the
US National Institute of Standards and Technology:
Acoustic thermometry (based on the
speed of sound in
argon gas),
photonic thermometry (based on the
thermal expansion of a
Bragg grating in an
optical fibers),
radiation thermometry (based on the Planck radiation law), and
Johnson noise thermometry.
Since electrical current is the movement of
electrons, it's reasonable to conclude that the thermal motion of electrons would create a current; and, since these motions are
random, the current is a
noise current. In 1928,
John B. Johnson of
Bell Labs was the first to measure this noise, often called the
Johnson-Nyquist noise.[2]
Physicist,
Harry Nyquist, also of Bell Labs, did a
theoretical study of these currents,[3] and his
equation for the
root mean square (RMS) noise voltage
vn for a resistor
R at absolute temperature
T is as follows,
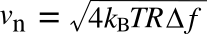
where
Δf is the
bandwidth in
hertz over which the noise is measured, and k
B is the
Boltzmann constant. The noise voltage is small. A 1
k-ohm resistor at room temperature, measured over a 10 kHz bandwidth, has an
RMS noise voltage of just 400
nanovolt. Of course, today's sensitive
electronic amplifiers make measurement of such noise voltages very easy. Johnson noise thermometers are small, easy to make, and they can be quite sensitive. The NIST web site reports that a 40 μK/K absolute uncertainty was achieved in 2010 at 505 K and 693 K.[4]
Since there are absolute standards for
resistance (via
the quantum Hall effect) and
frequency, and since temperature can be measured by other means, the Nyquist equation can be used to obtain a value for the Boltzmann constant, provided that there's a way to measure the rms noise voltage.[5-8] This is typically accomplished by comparing the noise signal with that of a
quantum voltage noise source (QVNS).
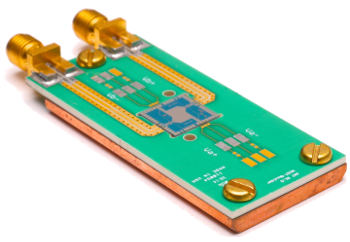
NIST quantum voltage noise source (QVNS).
The QVNS provides a noise signal that can be compared to the Johnson noise of a resistor.
(NIST photo by Dan Schmidt.
The reason for wanting a precise value of the Boltzmann constant is that this constant will be given a fixed value in 2018 in order for the unit of absolute temperature, the
kelvin, to be defined based on the Boltzmann constant. Presently, k
B is defined using acoustic gas-thermometry.[5]
In one study, the noise voltage from a Johnson noise thermometer based on a 200-Ohm resistor was compared to the voltage from a quantum voltage noise source at the
triple point of water. For a bandwidth of 550 kHz,
integrated over 33 days, a Boltzmann constant 1.380 651 4(48)x10
-23 joule/kelvin was obtained.[5] This value is offset just a few
ppm from the 2010 CODATA established value. A NIST study in 2017, also based on the Johnson noise thermometry but using a different
statistical analysis, gave a value of 1.380 641 0(81)x10
-23 joule/kelvin.[6]
NIST
scientists have collaborated with
colleagues at the
National Institute of Metrology (Beijing, China) to generate a value for the Boltzmann constant with a relative uncertainty of 2.8 parts per million.[7] The improved value was a result of better
shielding of the
experimental area from stray noise and upgrades to the electronics.[8] One other factor in the improved precision was an increase in the size of the resistor.[8] This new result has also been accepted for
publication in the
journal,
Metrologia.[6,7]
The present measurements that define the kelvin are 100 times less
accurate than those for the units of
mass and
electricity. The
kilogram, a notoriously difficult unit to measure, is known to
parts per billion, but the kelvin is known to just a part per million.[8] A redefinition the
International System of Units (SI) is expected at the end of 2018 at the
General Conference on Weights and Measures. At this redefinition, SI units will no longer rely upon physical objects, like the
international prototype kilogram, or
materials to define the measurement units. The new SI will be based strictly on
physical constants such as the
speed of light and the Boltzmann constant.[8]
The kelvin temperature unit is presently defined by the temperature of the triple point of water in a sealed glass cell. The triple point, where
ice,
water, and
water vapor exist in
equilibrium corresponds to 273.16 kelvins (0.01 degrees
Celsius or 32.0 degrees
Fahrenheit), and the kelvin is defined as 1/273.16 of the measured temperature value, since it spans the temperature domain down to absolute zero (0 K).[8]
Problems exist in this method, as in any experimental technique, from things such as
chemical impurities in the water, and even different
isotopes of
hydrogen and
oxygen from which the water
molecules are composed.[8] Says
Nathan Flowers-Jacobs, lead
author of the Metrologia paper,
"By defining the kelvin in terms of the Boltzmann constant, you don’t have to have these variations in uncertainty, and you can use quantum-mechanical effects."[8]
There are some restrictions on the Boltzmann constant measurement for it to be good enough to redefine the kelvin. There must be one experimental value with a relative uncertainty below one part per million, and there needs to be at least one measurement from a different technique that gives a relative uncertainty below three parts per million.[8] At present acoustical measurements have given the best accuracy.[8] Great confidence is given to a value when it's derived from different methods, multiple times.[8]
In 1999, NIST developed the QVNS as a voltage reference for Johnson noise thermometry. The QVNS is based on a
superconducting Josephson junction, and it provides a fundamentally accurate noise voltage signal, since it produces quantum mechanical noise. The resistor noise voltage is measured in comparison to the QVNS noise, allowing a very accurate temperature measurement, and a measurement of the Boltzmann constant when the resistor is held at a known temperature.[8]
References:
- Thermometry Web Page, NIST Web Site.
- J. Johnson, "Thermal Agitation of Electricity in Conductors", Phys. Rev. 32 (1928), pp. 97ff.
- H. Nyquist, "Thermal Agitation of Electric Charge in Conductors", Phys. Rev. vol. 32 (1928), pp. 110ff.
- Johnson Noise Thermometry, NIST Web Site.
- Jifeng Qu, Samuel P Benz, Alessio Pollarolo, Horst Rogalla, Weston L Tew, Rod White, and Kunli Zhou, "Improved electronic measurement of the Boltzmann constant by Johnson noise Thermometry," arXiv, December 31, 2014.
- J. Qu, S. Benz, K. Coakley, H. Rogalla, W. Tew, D. White, K. Zhou and Z. Zhou, "An improved electronic determination of the Boltzmann constant by Johnson noise thermometry," Metrologia, vol. 54, no. 4 (August, 2017), https://doi.org/10.1088/1681-7575/aa781e.
- N.E. Flowers-Jacobs, A. Pollarolo, K.J. Coakley, A.E. Fox, H. Rogalla, W. Tew and S. Benz, "A Boltzmann constant determination based on Johnson noise thermometry," Metrologia, vol. 54, no. 5 (October 2017).
- NIST 'Noise Thermometry' Yields Accurate New Measurements of Boltzmann Constant, NIST Press Release, June 29, 2017.
Permanent Link to this article
Linked Keywords: Temperature; laboratory; panoply; thermometer; temperature-measuring instrument; platinum-rhodium thermocouple; voltage; room temperature; platinum; resistance thermometer; electrical resistance; electromagnetic radiation; infrared; visible spectrum; Planck's law; spectral density; black body; thermal equilibrium; wavelength; Wikimedia Commons; Darth Kule; hot wire pyrometer; telescope; crucible; eyepiece; metal; wire; electric current; color; emissivity; calibration; calibrated; thermodynamic temperature; gas thermometer; thermodynamics; Charles' Law; volume; ideal gas; pressure; proportional; absolute temperature; atmospheric pressure; helium; ideal gas; inert gas; monatomic gas; Inkscape; physical property; temperature measurement; website; US National Institute of Standards and Technology; acoustic-thermometry; speed of sound; argon; photonic thermometry; thermal expansion; fiber Bragg grating; optical fiber; radiation thermometry; Johnson noise thermometry; electron; randomness; random; noise; John B. Johnson; Bell Labs; Johnson-Nyquist noise; physicist; Harry Nyquist; theory; theoretical; equation; root mean square (RMS); bandwidth; hertz; Boltzmann constant; ohm; k-ohm; nanovolt; electronic amplifier; electrical resistance; quantum Hall effect; frequency; quantum voltage noise source; NIST; Johnson noise; Dan Schmidt; kelvin; triple point of water; integral; integrated; joule; ppm; statistical analysis; scientist; collaboration; colleague; National Institute of Metrology (Beijing, China); electromagnetic shielding; experiment; experimental; scientific literature; publication; scientific journal; Metrologia; accuracy and precision; accurate; mass; electricity; kilogram; parts per billion; International System of Units; General Conference on Weights and Measures; international prototype kilogram; material; physical constant; speed of light; ice; water; water vapor; equilibrium; Celsius; Fahrenheit; chemical impurity; isotope; hydrogen; oxygen; molecule; Nathan Flowers-Jacobs; author; quantum mechanics; quantum-mechanical; superconducting; Josephson effect; Josephson junction.