Collision Avoidance
November 27, 2017
One common element of
romance novels is the first meeting of
destined lovers: "Their eyes met from across the room, and they were drawn to each other by an
irresistible force."
Gravitation behaves in a similar fashion, albeit on a lesser scale. While the far stronger
coulombic force between
charged particles can be
repulsive as well as
attractive, gravitation can only be attractive. We can suppress
electric forces, but not gravitational forces (No,
weightlessness, or
free-fall, is not a
counterexample).
Science fiction enjoys negation of conventional
physics in such things as
time travel, and
H. G. Wells decided to negate gravitational force in his 1901
novel,
The First Men in the Moon. In this novel, a
reclusive scientist invents Cavorite, a
material that acts as a gravitational shield that allows travel to the
Moon. At the Moon, they discover an
extraterrestrial civilization of
insect-like Selenites.

Inspiration for Zardoz?
This is the cover illustration of the first edition of H. G. Wells', The First Men in the Moon.
The 1964 film adaptation of this novel is notable for the stop-motion animation effects of Ray Harryhausen (1920-2013).
(Wikimedia Commons image, colorized for artistic effect.)
While lovers would enjoy
colliding in their
traverse through room space, most of the time people try to avoid other people while they are walking towards each other, as on a
sidewalk. Fortunately, there's an established
convention that approaching people will veer to the
right to avoid collision. This convention is also followed in
aircraft visual flight rules (VFR), which specify that two aircraft flying head-on will each move to their right.
You can imagine
pedestrian collision avoidance to take many forms depending on how closely a person would want to be to another. Such a simple problem inspired my attempt at a simple
computer simulation. I decided to use the same
inverse-square law that governs the force between repulsive charges, with a change in the
force constant determining how closely the approaching people interact. Such physical
modeling of pedestrians as interacting particles with repulsive forces has a long
history.[1]
In my simulation (
C language source code here), our two pedestrians start from opposite corners of a room and attempt to reach their far corner. As they approach each other, they veer to their right (actually, towards the opposite wall on their right, since it's easier to
program) with an
intensity proportional to the inverse square of the distance between them. After passing each other, since knowledge of the direct path that they would have taken is not possible (there are no
diagonals painted on the floor), they take the most direct path to their intended corner after the deviation caused by avoidance (see figure).
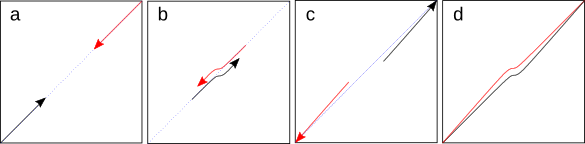
Pedestrian collision avoidance simulation. a) The two pedestrians are oblivious to each other and walk directly to their opposite corners. b) As they approach each other, their inverse-square law avoidance kicks in. c) After passing each other, they walk directly towards their intended corner. d) The complete paths taken by the two pedestrians. (Data from my C language program.)
Real pedestrians are unlikely to follow an inverse-square avoidance.
Mathematicians from the
Institut für Mathematik of the
Universität Würzburg (Würzburg, Germany) and the
Université Côte d'Azur (Nice, France) have taken a more advanced approach to this problem by utilizing a
statistical mechanics approach afforded by the
Fokker–Planck equation.[2-4] This
partial differential equation was originally used to describe the
time evolution of the
probability density of particles in
Brownian motion.
While
Max Planck (1858-1947) is known to most scientists for his discovery of
the quantum of energy,
Adriaan Fokker (1887-1972) is not as well known. Better known is his
cousin,
aeronautical engineer,
Anthony Fokker, founder of the
eponymous aircraft company,
Fokker. Adriaan Fokker had a superb physics background, obtaining his
Ph.D. in 1913 under
Hendrik Lorentz at the
University of Leiden. The Fokker–Planck equation was derived in his
thesis.
Fokker contributed to
special and
general relativity, but he later became interested in
music theory during the
Second World War. This was a reaction to the closing of the University of Leiden, where he worked, during the war. While the
equal-tempered twelve-tone scale is the foundation of
western music, Fokker took an interest in the 31-note equal-tempered scale first
researched by
Christiaan Huygens.[5] The 31-note equal-tempered scale is notable for having an
harmonic seventh. The
seventh in the twelve-tone scale differs from 15/8 by about one
cent. Fokker composed some 31-note equal-tempered music, and he built the Fokker organ, a 31-tone equal-tempered organ.

Assembly of physicists at the Kamerlingh-Onnes Laboratory, Leiden, 1926. Adriaan Fokker appears in the first row, fifth from the left, next to Hans Kramers (sixth from left), and Samuel Goudsmit (far right). Other notables are P.A.M. Dirac, second row, second from the left, J. Robert Oppenheimer (third from the left), and Paul Ehrenfest (fifth from left). (Via Wikimedia Commons)
While my model involved collision avoidance when pedestrians approached head-on, the Würzburg and Côte d'Azur mathematicians examined
intersecting paths. In the Fokker–Planck model framework that incorporates aspects of
Nash equilibrium game theory, the probability density functions of the two pedestrians are considered. A
differential game is formulated, the goal of which is to
minimize the
cost associated with collision avoidance. The research team demonstrated equilibrium solutions that compare favorably with the outcome of
experiments conducted with actual pedestrians.[2]

Collision theory can apply to more than just pedestrians.
Wikimedia Commons image by Shuets Udono (modified).
Game theory is a new approach to this long standing collision problem, and it seeks to minimize the cost of collision avoidance.[4] The cost is easily described by the idea that if one of the pedestrians chooses not to modify his course, forcing the other to do all the avoidance, the pedestrian who does all the avoidance would think he was treated unfairly.[4] A Nash equilibrium is reached when each pedestrian chooses exactly the one
strategy that gives the best possible solution for both of them. As
Alfio Borzi,
Chair of Mathematics IX (Computational Science) at the University of Würzburg, summarizes,
"When the paths of two pedestrians cross, it basically comes down to the following question: What is the optimal solution of this conflict that is satisfactory for both parties... Each player gets the best possible solution, so they are all happy."[4]
The motions of the two pedestrians are assumed to be
stochastic drifts along a path with a
control function.[2] The Fokker-Planck equation describes the
probability of possible motions of a pedestrian from a starting to finishing point.[4] It was found that the
calculated paths were strikingly similar to paths taken by actual pedestrians.[4]
Such modeling can aid in the design of
town squares, and the design of
escape routes that are effective even in the event of a
mass panic.[4] Says Borzi, "There are signs in current research that more and more fields of
biology can be described with this
theory," an example being when two
animal populations compete for one
habitat.[4]
References:
- Dirk Helbing, A mathematical model for the behavior of pedestrians, "Behav. Sci. vol. 36, no. 4 (October, 1991), pp. 298-310, doi:10.1002/bs.3830360405.
- S. Roy, A. Borzì, and A. Habbal, "Pedestrian motion modelled by Fokker–Planck Nash games," Royal Society Open Science, vol. 4, article no. 170648, September 13, 2017, DOI: 10.1098/rsos.170648. This is an open access article with a PDF file available here.
- Supplementary material for ref. 2.
- Gunnar Bartsch, "On a collision course with game theory," Universität Würzburg Press Release, September 22, 2017.
- Anton de Beer, "The Development of 31-Tone Music," Sonorum Speculum, 1965, via the Huygens-Fokker Foundation Web Site.
Linked Keywords: Romance novel; destiny; destined; love; lovers; irresistible force; Newton%27s law of universal gravitation; Coulomb's law; coulombic force; charged particle; electrostatics; repulsive; attractive; electric force; free-fall; counterexample; science fiction; physics; time travel; H. G. Wells; novel; The First Men in the Moon; recluse; reclusive; scientist; invention; invent; gravitational shielding; Cavorite; material; Moon; extraterrestrial civilization; insect; Selenite; inspiration; Zardoz; film adaptation; stop-motion animation; Ray Harryhausen (1920-2013); Wikimedia Commons; film colorization; colorize; collision; collide; translation; traverse; sidewalk; convention; relative direction-right; aircraft visual flight rules; pedestrian; computer simulation; inverse-square law; force constant; modeling; history; C programming language; source code; avoidance.c; computer programming; program; intensity; proportionality; proportional; diagonal; mathematician; Institut für Mathematik; Universität Würzburg (Würzburg, Germany); Université Côte d'Azur (Nice, France); statistical mechanics; Fokker–Planck equation; partial differential equation; time evolution; probability density function; Brownian motion; Max Planck (1858-1947); quantum mechanics; quantum of energy; Adriaan Fokker (1887-1972); cousin; aeronautical engineer; Anthony Fokker; eponymous; aircraft company; Fokker; Doctor of Philosophy; Ph.D.; Hendrik Lorentz; University of Leiden; thesis; special relativity; general relativity; music theory; World War II; Second World War; equal temperament; equal-tempered; chromatic scale; twelve-tone scale; classical music; western music; research; Christiaan Huygens; harmonic; major seventh; B (musical note); seventh; cent (music); physicist; Kamerlingh-Onnes; laboratory; Leiden; Hans Kramers; Samuel Goudsmit; P.A.M. Dirac; J. Robert Oppenheimer; Paul Ehrenfest; intersection; intersecting; Nash equilibrium game theory; differential game; mathematical optimization; minimize; opportunity cost; experiment; Shuets Udono; game theory; strategy; Alfio Borzi; Chair of Mathematics IX (Computational Science) at the University of Würzburg; stochastic; control loop; control function; probability; calculation; calculated; town square; emergency evacuation; escape routes; mass panic; biology; theory; animal; population; habitat.