Torricelli's law
January 23, 2017
Vacuum chambers are a staple of nearly every
solid state physics laboratory. I had several in my own laboratory for such purposes as
physical vapor deposition,
electron beam excitation of
phosphors, and
high voltage testing of
electrical insulators. While those systems achieved vacuums in the range of 10
-9 atmospheres, my
colleagues doing
molecular beam epitaxy had systems that achieved a vacuum several
orders of magnitude better than that.
What do such vacuum pressures mean when you're doing an
experiment? There's a
physical constant, called
Loschmidt's number, that's the number of
molecules in an
ideal gas in a
volume at
standard temperature and pressure, 0
°C (273.15 K) and 100
kPa (about one atmosphere). This is 2.687 x 10
25 per
cubic meter. This constant is named after the
Austrian physicist,
Johann Josef Loschmidt (1821-1895), who gave the first
estimate of the
size of molecules.

Commemorative plaque at the house in which Loschmidt lived from 1890-1895.
Loschmidt is famous, also, for Loschmidt's paradox that the time-reversal symmetry of particle motion in classical mechanics is at odds with our observation that entropy is always increasing.
(Photo by Wolfgang Dvorak, via Wikimedia Commons.)
An
ultra high vacuum system of the type suitable for molecular beam epitaxy, achieves a vacuum of about 10
-12 atmospheres.
Calculation using Loschmidt's number shows that even at a vacuum of 10
-12 atmospheres there are still 2.687 x 10
13 gas molecules per cubic meter in our vacuum chamber. Most vacuum chambers are just a tenth of this volume, so we're dealing with about 10
12 molecules. This still seems large, but a
square centimeter of the surface of a typical
(110) silicon wafer contains about 10
15 atoms, and not every molecule in the atmosphere will contact the surface.
In my laboratory, my
vacuum gauges didn't give the pressure in atmospheres. The typical laboratory unit of vacuum pressure is the
torr, named after the
Italian physicist,
Evangelista Torricelli (1608-1647). Torricelli invented the
mercury barometer, and his device also demonstrated why
water can't be raised more than ten
meters by a
pump. That's because the pushing force on the water column is the
differential pressure between the pump and the atmosphere, and it will attain a maximum at a perfect vacuum.
In
analogy to water pumping, Torricelli's barometer could be used as a vacuum gauge in which the height of the mercury in a column showed the strength of the vacuum; thus,
millimeters of mercury was a measure of vacuum, and this measure, now quantified as 101325/760
pascals ≈ 133.3 Pa, is known as a torr in his honor. The 760 comes from the typical height of mercury in a barometer exposed to the atmosphere, and the 101,325 is the number of pascals in an atmosphere.

Italian physicist, Evangelista Torricelli (1608-1647).
(Portrait at the Museo Galileo of Florence, via Wikimedia Commons.)
Torricelli, who apparently enjoyed explaining
hydraulics using the physics of
mechanics, is also famous for
Torricelli's law that explains how fast fluid will flow out of a hole in its container. Most readers may have discovered the fact that fluid flows more quickly through a
funnel if it's always topped-off, and this is quantified by Torricelli's law.
Torricelli found that the
speed at which a fluid exits a hole in a container is a
function of the height of the fluid above the hole, a simple consequence of
gravity. According to this law, the exit speed
v is given as
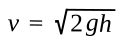
where
g is the
gravitational acceleration, about 9.8 m/sec
2 at
Earth's surface, and
h is the height of the fluid above the hole.
I've always enjoyed doing simple experiments at
home, and it was fun advising my
children when they were doing their
school science fair projects. Seeing the popular
cookbook, "
The Joy of Cooking," in our
kitchen made me think about publishing a "Joy of Experiment" book. Alas, I was preempted in 2011 by publication of the book, "The Joy of Physics," by Arthur W. Wiggins.[1] However, I was still inspired to verify Torricelli's Law using a
computer for
data acquisition. A
schematic of the experiment appears below.
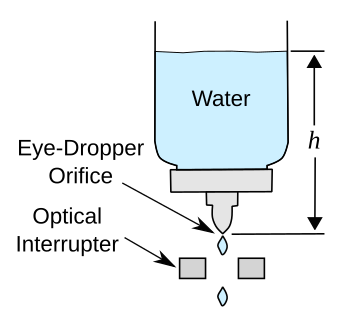
My experiment to test Torricelli's law.
The optical interrupter is connected to a computer to count droplets as they fall through the gap.
(Drawn using Inkscape.)
In this experiment, the drop rate is the equivalent of the flow rate, and the
data analysis is straightforward. The container held about three
cups of water (about 700
mL), the initial fluid level was four
inches, and it was reduced to one inch over the course of the experiment. As can be seen by the results shown in the next two
graphs, Torricelli's Law seems to be true over this small change in fluid height.
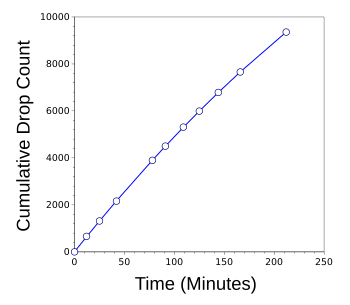
Cumulative count rate of water drops as the fluid level decreased from four inches to one inch.
Although not visually apparent from this graph, the drop rate decreased considerably.
(Graphed using Gnumeric.)
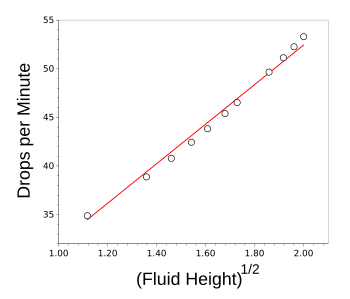
The linear fit is what would be expected from Torricelli's Law.
(Graphed using Gnumeric.)
As can be deduced from its simplicity, the equation for Torricelli's Law is the solution for an idealized case. One ignored factor is the interaction between the fluid and the
material of the container and the exit
orifice. This interaction was addressed in a recent
paper in
Physical Review Letters by physicists at the
École Normale Supérieur de Lyon (Lyon, France), who found that the
hydrophilicity of the exit orifice affects the draining rate. [2-3] They've shown that the hydophilic property of the container's surface also plays a role, explaining why identically shaped tanks will empty at different rates.[3]
One surprising result of their experiments was that the exit speed goes through a minimum as the surface property of the bottom plate of the container changes from hydrophilic to
hydrophobic.[2] Maximum slowing, about 20%, was achieved at a static
wetting angle (contact angle) of about 60°. The experiments suggest that cause of this
phenomenon is the
meniscus that forms at the exit outlet.[2] The research team was able to develop a simple
model to predict the drainage speed as a function of the static wetting angle.[2]
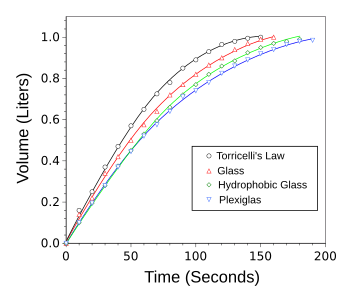
Deviation from Torricelli's Law caused by the hydrophilicity of the container bottom plate.
The initial fluid volume was 1 liter, and the initial fluid height was 10 cm.
(Graphed using Gnumeric from data in ref. 2.[2]
The presence of the meniscus causes an accelerated draining rate compared to a completely straight jet.[3] The degree of acceleration depends on the shape of the meniscus, thus the importance of the hydrophilicity.[3]
References:
- Arthur W. Wiggins, "The Joy of Physics," Illustrations by Sydney Harris, Prometheus Books, 466 pp., March 2, 2011, ISBN-13: 978-1616144531 (via Amazon). Preview at Google Books.
- J. Ferrand, L. Favreau, S. Joubaud, and E. Freyssingeas, "Wetting Effect on Torricelli's Law," Phys. Rev. Lett., vol. 117 (December 7, 2016), Article no. 248002, DOI:https://doi.org/10.1103/PhysRevLett.117.248002.
- Katherine Wright, "Synopsis: Wetting Matters When Emptying a Tank," Physics, December 7, 2016.
Permanent Link to this article
Linked Keywords: Vacuum chamber; solid state physics; laboratory; physical vapor deposition; electron beam; excited state; excitation; phosphor; high voltage; electrical insulator; atmosphere; colleague; molecular beam epitaxy; orders of magnitude; experiment; physical constant; Loschmidt constant; Loschmidt's number; molecule; ideal gas; volume; standard temperature and pressure; Celsius; °C; Pascal; kPa; cubic meter; Austria; Austrian; physicist; Johann Josef Loschmidt (1821-1895); approximation; estimate; size of molecules; commemorative plaque; Loschmidt's paradox; T-symmetry; time-reversal symmetry; classical mechanics; entropy; entropy production; Wolfgang Dvorak; Wikimedia Commons; ultra high vacuum; calculation; square centimeter; Miller index; (110); silicon wafer; atom; vacuum gauge; torr; Italy; Italian; Evangelista Torricelli (1608-1647); mercury; barometer; water; meter; pump; differential pressure; analogy; millimeter; Museo Galileo of Florence; hydraulics; mechanics; Torricelli's law; funnel; speed; function; gravitation; gravity; gravitational acceleration; lithosphere; Earth's surface; home; child; children; school science fair; cookbook; The Joy of Cooking; kitchen; computer; data acquisition; schematic; experiment; slotted optical switch; optical interrupter; Inkscape; data analysis; cup; litre; mL; inch; Cartesian coordinate system; graph; Gnumeric; data; square-root; curve fitting; linear fit; material; nozzle; orifice; scientific literature; paper; Physical Review Letters; École Normale Supérieur de Lyon (Lyon, France); hydrophile; hydrophilicity; hydrophobe; hydrophobic; wetting angle; contact angle; phenomenon; meniscus; mathematical model; Arthur W. Wiggins, "The Joy of Physics," Illustrations by Sydney Harris, Prometheus Books, 466 pp., March 2, 2011, ISBN-13: 978-1616144531.