The Square Root of Two
June 6, 2016
As an
undergraduate, I encountered quite a few interesting people from among both
students and
professors. There was the
economics professor who wore the same
necktie with a
graph paper motif every day. There was the
physics graduate student teaching assistant who began our first session by placing a
trash can on his
desk and saying, "
elephant." He explained that was his way of ensuring that he would be remembered. He was right.
One of my student acquaintances was so
comical, he should have made a
career as a
late night television host, and not as an
engineer. One of his
routines was to
mimic the
lectures of a certain professor. He would write furiously on a
blackboard, stop, tap the
chalk on a particular
equation, look towards his
audience, and exclaim, "Take
square root... Take square root!"
The
square root of two (1.4142135623..., sequence no.
A002193 in the
On-Line Encyclopedia of Integer Sequences) is an
irrational number; that is, it can't be expressed as a
ratio of
integers. The integers include the
natural numbers.
Early
mathematicians considered
negative numbers to be absurd. For that reason, all their fractions involved ratios of natural numbers, only. While the word, "
absurd," means irrational, "
surd" is actually a mathematics term relating to the roots of equations.

Thales (624-546 BC, top) and Pythagoras (570-495 BC, bottom) were among the earliest mathematicians.
Thales is known for Thales' theorem that any angle inscribed in a semicircle is a right angle. He is also reported to have measured the height of the Egyptian pyramids using the concept of 45° similar triangles.
Pythagoras is known, of course, for the Pythagorean theorem. He invented the geometrical object known as the Tetractys.
(Thales image (top), and Pythagoras image (bottom), from the Nuremberg chronicle, via Wikimedia Commons.)
Natural numbers are called that for the simple reason that they are the
counting numbers. What can be more
natural than looking out a
window and thinking, "One
tree, two trees, three trees...?" The
German mathematician
Leopold Kronecker, who is known to
scientists and
engineers for his
Kronecker delta function, and among mathematicians for giving
Georg Cantor such a hard time, once said that "
God made the integers, all else is the work of
man."[1]
Pythagoras made the discovery that
musical instrument strings having integral
fraction lengths were most
harmonious. Instruments with
Pythagorean tuning have
tones anchored at a
perfect fifth in which the
G-note string in a
C-major scale is 2/3 the length of the
C-string. The modern evolution of this concept is
just intonation, where all the notes are ratios of small natural numbers, as seen in the table.
| C |
| D |
| E |
| F |
| G |
| A |
| B |
| 1/1 |
| 9/8 |
| 5/4 |
| 4/3 |
| 3/2 |
| 5/3 |
| 15/8 |
The followers of Pythagoras, the
Pythagoreans, believed that everything in the
universe could be related to the natural numbers and their ratios; so, it came as quite a surprise when
Hippasus (c. 450 BC) showed that the length of the
hypotenuse of an
isosceles right triangle could not be expressed as a ratio of natural numbers. When the sides of such a triangle are of length one, this means that the square root of two is irrational. There's a
legend that the
gods caused Hippasus to be
drowned at
sea as
punishment for this revelation.

Hippasus of Metapontum
Not much is known about Hippasus, other than his being a Pythagorean.
The years of his birth and death are not known, although it's likely that he lived in the 5th century BC, about a century after Pythagoras.
(Engraving, circa 1820, by G. Boccanera, via Wikimedia Commons.)
The method of
proof employed by Hippasus is known as
reductio ad absurdum. In this method, a proposition is shown to have two incompatible qualities, such as a
number being both
odd and
even. This proof in the context of Hippasus's triangle is tedious, so it won't be explained here. You can
read it on Wikipedia. I'll give a proof in modern notation, which is easier to understand.
First, we suppose that the square root of two really is rational, so it can be written as the ratio of two integers,
p and
q. We suppose the fraction has been
reduced by canceling all
common factors of
p and
q.
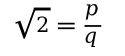
We then
square both sides of the equation.
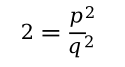
Rearranging the equation, we see that
p2 must be an even number.
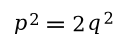
If
p2 is even, then
p is even. You can see that this is true, since having a 1, 3, 5, 7, or 9 as the last digit of
p would give 1, 9, 5, 9, or 1 as the last digit of
p2. If
p is even, then
p2 is
divisible by four, so
q2 and
q must be even.
Now comes the
reductio ad absurdum part. We showed that both
p and
q are even, which contradicts our requirement that the initial fraction was properly reduced. Since our analysis gives this false result, then our initial assumption that the square root of two is rational is also false.
The date for the Greek proof of the irrationality of the square root of two is about 450 BC. The Greeks, however, weren't the only people doing mathematics in antiquity. As I wrote in a
recent article (Mathematical Astronomy in Babylon, March 10, 2016), the
Babylonians were adept at the use of mathematics in astronomy from a very early date.
Benjamin M. Altschuler of the
The Fieldston School (Bronx, New York), and
Eric L. Altschuler of the
Lewis Katz School of Medicine at Temple University (Philadelphia, Pennsylvania), have just presented evidence that a
clay tablet from the
Old Babylonian Empire (20th - 16th centuries BC) may contain a geometrical construction leading to a proof of the irrationality of the square root of two similar to that of Hippasus.[2]
This tablet, known as BM 15285,[3] contains 41 geometrical
area problems. Problem twelve, as shown in the figure, has the following associated text: "The side of the
square is 60
rods. Inside it [I drew]16 wedges [triangles]. What are their areas?"[2] The figure does not accompany an explicit proof of the irrationality of the square root of two, but the authors explain that its essential elements are there. See the
arXiv paper for details.[2]
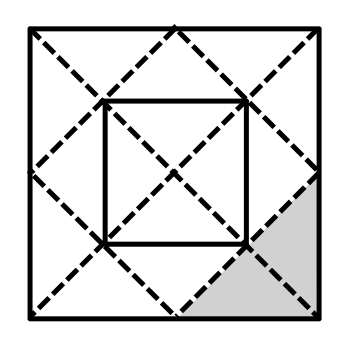
Problem xii of tablet BM15285.
The shaded area is a missing part of the tablet.
(Drawn using Inkscape.)
![]()
References:
- "Die ganzen Zahlen hat der liebe Gott gemacht, alles andere ist Menschenwerk."
- Benjamin M. Altschuler and Eric L. Altschuler, "Proof of the Irrationality of the Square Root of Two in Babylonian Geometry Problem Tablets," arXiv, March 22, 2016.
- Images of Babylonian tablet BM15285, PDF file at the University of Helsinki.
Permanent Link to this article
Linked Keywords: Undergraduate; student; professor; economics; necktie; graph paper; motif; physics; postgraduate education; graduate student; teaching assistant; waste container; trash can; desk; elephant; comedy; comical; career; late night television host; engineer; sketch comedy; routine; impressionist; mimic; lecture; blackboard; chalk; equation; audience; square root; square root of two; A002193; On-Line Encyclopedia of Integer Sequences; irrational number; ratio; integer; natural numbers; mathematician; negative number; absurd; surd; Thales; Pythagoras; Thales' theorem; angle; semicircle; right angle; Egyptian pyramids; similar triangles; Pythagorean theorem; geometry; geometrical; Tetractys; Nuremberg chronicle; Wikimedia Commons; counting numbers; nature; natural; window; tree; German; Leopold Kronecker; scientist; engineer; Kronecker delta function; Georg Cantor; God; man; musical instrument; string; fraction; harmony; harmonious; Pythagorean tuning; musical note; tone; perfect fifth; G-note string; C-major scale; just intonation; musical note C; musical note D; musical note E; musical note F; musical note G; musical note A; musical note B; Pythagoreanism; Pythagorean; universe; Hippasus (c. 450 BC); hypotenuse; isosceles triangle; right triangle; legend; deity; god; drowning; drown; sea; punishment; Metapontum; 5th century BC; century; mathematical proof; reductio ad absurdum; number; odd; even; Ancient Greece; irreducible fraction; reduce; factorization; common factors; square; divisor; divisible; Babylonia; Babylonians; The Fieldston School (Bronx, New York); Eric L. Altschuler; Lewis Katz School of Medicine at Temple University (Philadelphia, Pennsylvania); clay tablet; Old Babylonian Empire; area; square; rod; arXiv; Inkscape.