Granular Entropy
March 14, 2016
For my
dissertation, many
decades ago, I measured the high
temperature reaction of
metals forming
alloys. To do this, I teamed with a
graduate student colleague to construct a high temperature
calorimeter. Fortunately, he was good at doing
mechanical things, like wrestling with
vacuum systems, while I had a talent for
electronics, so the system performed its intended task. Eventually, I was able to build a second system to increase
throughput (see figure).

Old school calorimetry. The experiments were conducted in a vacuum system (left). The samples, sealed in quartz glass ampoules, were placed in chambers in a thermalizing block with their associated references (right), and heated with a tantalum wire heating coil (center). The power supply to the heater was 50 amps at 115 volts, or more than 5 kilowatts. (Photos by author. Click for larger image.)
In explaining one of his results, my colleague invoked
entropy. As we talked about this, I realized that I didn't know the relative importance of entropy in
thermodynamics. Sure, I knew all the
textbook equations from several
statistical mechanics and thermodynamics courses, but I had no idea whether entropy had a small or large affect on things such as the
heat of formation (a.k.a.,
enthalpy of formation) of a
compound.
The assess the importance of enthalpy, let's look at a simple process, the
evaporation of a
material such as
aluminum. Since
boiling is an
equilibrium phase transformation in which the
liquid and
gas phases coexist, the
Gibbs free energy change
ΔG of the transformation is zero,
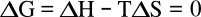
where
ΔH is the
enthalpy of vaporization, and
ΔS is the
vaporization entropy. We can see that entropy is just as important as enthalpy, at least in this example of boiling, since the terms are equal.
Entropy is a strange property of matter that arises from the principle that objects can be arranged in different ways.
Students of
physics and
chemistry are familiar with
Boltzmann's entropy formula,

in which
S is the
entropy,
KB is the
Boltzmann constant (1.38062 x 10
-23 joule/
kelvin), and
Ω is the number of states accessible to a system.

Ludwig Boltzmann, as depicted on a 1981 Austrian stamp.
Boltzmann apparently suffered from an untreated bipolar disorder, as confirmed by his student, Lise Meitner. His death was a suicide.
(Via Wikimedia Commons))
The Boltzmann entropy formula is actually a simplification of the
Boltzmann-Gibbs entropy when every state has the same
probability pi; viz.,

Both of these equations define a maximum entropy, a consequence of the equal probability of stuffing an
atom or
molecule into any accessible state.
While we usually think of entropy in terms of atoms and molecules where their huge numbers give large entropy values, we can apply the entropy concept, also, to smaller assemblages of larger particles constrained in a
volume. Granular materials have become an important
research area in physics, so the question arises as to what entropy value a handful of such
macroscopic scale particles might have. That's a question answered in a recent study by
chemists at the
University of Cambridge (Cambridge, United Kingdom).[1-2]
The press release for this research figuratively asks, "How many ways can you arrange 128
tennis balls (in a fixed volume)?" and the answer is the huge number 10
250. This number greatly exceeds the total number of
atoms in the
universe, which is
estimated to be 1080. The
packing is reminiscent of the
random packing of
oblate spheroids I discussed in an
earlier article (Packing, November 30, 2010).

A simple cubic lattice of tennis balls.
The arrangement of particles in the granular entropy study is disordered, and not like this regular array.
(Created from a basis image of Horia Varlan on Wikimedia Commons.)
The physics of granular materials has application to the understanding of the behavior of such materials as
soil,
sand, and
snow. Granular materials will only change their configuration after application of an external
force, and an understanding of their entropy could enable prediction of things such as
avalanches.[2] Says study
coauthor Stefano Martiniani of
St. John's College, Cambridge, "Granular materials themselves are the second most processed kind of material in the world after
water, and even the shape of the
surface of the Earth is defined by how they behave."[2]
Calculation of the configurational entropy of a granular system is so complex that it was never attempted for a system of more than about twenty particles.[2] The Cambridge team was able to increase this limit to 128 by building upon previous work.[3-4] An exhaustive
enumeration of particle states is not computationally tractable. Instead, the research team selected a small sample of configurations and calculated the
probability of their occurrence.[2] With this information, they were able to
estimate the total configurational entropy (see figure).
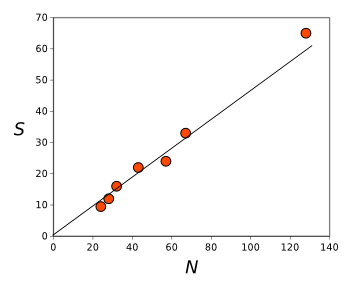
See a trend?
Configurational entropy as a function of system size N for three-dimensional jammed sphere packings.
The line is a linear fit of the data.
(Graphed using Gnumeric from data in ref. 1.[1]
This technique can be applied to other areas, including
machine learning, where it's useful to know all the different ways you can connect a system to process information.[2] As the authors state in the abstract of their paper, the technique "should be applicable to a wide range of other enumeration problems in
statistical physics,
string theory,
cosmology, and machine learning..."[1] Says Martiniani,
"Because our indirect approach relies on the observation of a small sample of all possible configurations, the answers it finds are only ever approximate, but the estimate is a very good one... By answering the problem we are opening up uncharted territory. This methodology could be used anywhere that people are trying to work out how many possible solutions to a problem you can find."[2]
References:
- Stefano Martiniani, K. Julian Schrenk, Jacob D. Stevenson, David J. Wales, and Daan Frenkel, "Turning intractable counting into sampling: Computing the configurational entropy of three-dimensional jammed packings," Phys. Rev. E, vol. 93, no. 1 (January, 2016), Document no. 012906, DOI:http://dx.doi.org/10.1103/PhysRevE.93.012906.
- How many ways can you arrange 128 tennis balls? Researchers solve an apparently impossible problem, St. John's College, Cambridge, Press Release, January 27, 2016.
- Ning Xu, Daan Frenkel, and Andrea J. Liu, "Direct Determination of the Size of Basins of Attraction of Jammed Solids," Phys. Rev. Lett., vol. 106, no. 24 (June 17, 2011), Document no. 245502.
- Daniel Asenjo, Fabien Paillusson, and Daan Frenkel, "Numerical Calculation of Granular Entropy," Phys. Rev. Lett., vol. 112, no. 9 (March 7, 2014), Document no. 098002.
Permanent Link to this article
Linked Keywords: Thesis; dissertation; decade; temperature; chemical reaction; metal; alloy; postgraduate education; graduate student; colleague; calorimeter; mechanical; vacuum chamber; vacuum system; electronics; throughput; calorimetry; experiment; sample; fused quartz; quartz glass; ampoule; thermalisation; thermalize; reference; tantalum; wire; power supply; ampere; amps; volt; kilowatt; entropy; thermodynamics; textbook; equation; statistical mechanics; standard enthalpy of formation; heat of formation; enthalpy; chemical compound; evaporation; material; aluminum; boiling; thermodynamic equilibrium; phase transition; phase transformation; liquid; gas; phase; Gibbs free energy; enthalpy of vaporization; vaporization; student; physics; chemistry; Boltzmann's entropy formula; Boltzmann constant; joule; kelvin; Ludwig Boltzmann; Austria; Austrian; bipolar disorder; Lise Meitner; suicide; Wikimedia Commons; Boltzmann-Gibbs entropy; probability; atom; molecule; volume; granular material; research; >macroscopic scale; chemist; University of Cambridge (Cambridge, United Kingdom; tennis ball; universe; relative density; packing; randomness; random; oblate spheroid; simple cubic lattice; Horia Varlan; soil; sand; snow; force; avalanche; author; St. John's College, Cambridge; water; lithosphere; surface of the Earth; calculation; enumeration; probability; estimate; Gnumeric; machine learning; statistical physics; string theory; cosmology.