Measuring the Gravitational Constant
November 14, 2014
The
geek motif is not a recent
phenomenon.
Henry Cavendish (1731-1810), the prominent
British scientist who lived more than two
centuries ago, could rightly be counted among the geeks.
Technically competent, as are geeks of the present day, he was also exceptionally
shy. He was especially shy around
women, so much so that he communicated with his
female servants only by notes; and, according to
Wikipedia, he is said to have had a back door added to his
house so that he could leave without seeing the
housekeeper.

(Illustration by George Wilson, from "The Life of the Hon. Henry Cavendish," 1851, via Wikimedia Commons.)
Cavendish is credited with the discovery of
hydrogen, which he made by
dissolving metals in
acid; for example,
Fe + 2
HCl →
FeCl2 +
H2. He also reacted
carbonates with acid to get
carbon dioxide, which was called "fixed air" at that time. He concluded that
air was a 1:4 mixture of
oxygen ("dephlogisticated air") and
nitrogen ("phlogisticated air"). In his
experiments, Cavendish found a gas that wasn't oxygen or nitrogen existing at about the 1% level in air. This was later found by
William Ramsay and
Lord Rayleigh to be
argon.
Jumping from
chemistry to
physics, Cavendish did experiments on
electricity, discovering electrical principles that were later credited to others since he rarely
published. Our knowledge of these experiments have come through
James Clerk Maxwell, who was named the first
Cavendish Professor of Physics at
Cambridge University in 1871. Maxwell collected, edited, and published the
research papers of Cavendish in 1879.
Of special interest to physics is the
Cavendish experiment in which he determined the
density of the
Earth; and, indirectly, the value of the
gravitational constant G in
Newton's law of universal gravitation,
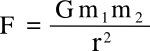
where
F is the gravitational
force between two
masses,
m1 and
m1, and
r is the distance between them. Although Cavendish calculated only the
density of the Earth, and not
G, the constant could be calculated from his
data. The present
CODATA value of
G is 6.67384 x 10
-11 m3 kg-1 s-2.
Cavendish obtained the
apparatus to do this experiment through a
serendipitous chain of events, as he detailed in the first paragraph of his paper on the measurement (see figure). Cavendish improved the apparatus to lessen the affects of
temperature and
air currents.

(Henry Cavendish, Esq. F. R. S. and A. S., "Experiments to Determine the Density of the Earth," Phil. Trans. R. Soc. Lond., vol. 88 (January 1, 1798), pp. 469-526, via Wikimedia Commons.)
I wrote about the Cavendish experiment in an
earlier article (Big G, October 12, 2010). A
schematic diagram of the experiment is shown in the figure. The larger
spheres,
cast from
lead, were each 350
pounds, while the smaller spheres, also of lead, were each 1.61 pounds. Such large masses notwithstanding, the force acting on the
torsion wire was just a ten millionth of a
newton. The torsion constant was obtained by measuring the
resonant frequency of the torsion assembly. The Cavendish value of
G was within a percent of the presently accepted value.
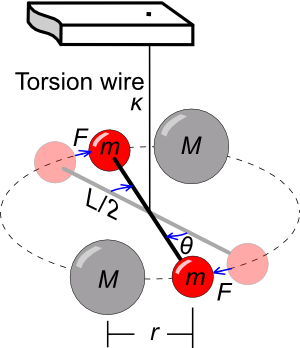
Schematic of the torsion balance used in the 1798 Cavendish experiment.
The larger masses (M) are stationary lead balls, and the smaller balls (m) are also made of lead.
Gravitational force causes the masses to twist the wire with torsion coefficient κ, which allows a force measurement.
(Diagram by Chris Burks, via Wikimedia Commons.)
Since gravitational force is so weak, the gravitational constant is the
fundamental constant known to the least
precision. There have been many attempts to improve on the Cavendish experiment, one recent example of which is given in the references.[1-2] As the figure shows, the experimental values for
G are consistent to just a few hundred
parts per million.
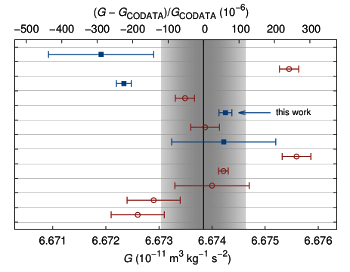
Measurement of G using torsion balances (circles) and other methods (squares). The shaded area is the one-sigma confidence interval of the 2010 CODATA value. Marked is the value of the University of Zürich experiment described below.
(Fig. 5 of ref. 3, modified, via arXiv.[3]
A
G experiment designed without a torsion balance was done by a team of seven
scientists at the
University of Zürich. This experiment, concluded in 2006, was a
decade in the making, and a summary of the experiment has been posted on
arXiv.[3] The original motivation for the experiment was the detection of a possible "
fifth force."[4] A fifth force has not been found, but the apparatus, shown conceptually in the figure, produced a new measurement of the gravitational constant.
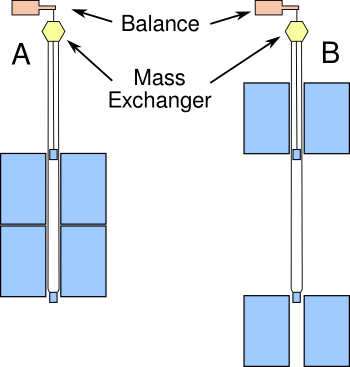
Schematic diagram of the University of Zürich gravitational constant measurement apparatus.
In configuration A, the weight of the top mass is increased, and the weight of the bottom mass is reduced, by the gravitational attraction of the large masses, while the reverse happens in B.
(Simplified version of fig. 5 of ref. 3, via arXiv.[3]
Attention to detail is important in a measurement like this. The large masses were 500
liter stainless steel vessels each filled with 6,760
kilograms of
liquid mercury. Liquid mercury was used, since
homogeneity of the masses could be assured, and mercury has a relatively high
density (13.54
g/cc). The smaller masses were
gold-plated oxygen-free, high-
conductivity (
OFHC)
copper about 1100 grams in mass. Copper was chosen to avoid any
magnetic forces.[3]
The gravitational signal in this experiment was large, with the differential force being about 7.7 μN. The value of
G obtained was 6.674 252 x 10
−11 m
3 kg
−1 s
−2 with a
relative standard uncertainty of 18 x 10
−6.[3]
References:
- Harold V. Parks, James E. Faller, "A Simple Pendulum Determination of the Gravitational Constant," arXiv Preprint (September 7, 2010).
- Eugenie Samuel Reich, "G-whizzes disagree over gravity," Nature, vol. 466, no. 7310 (August 26, 2010), p.1030.
- S. Schlamminger, R.E. Pixley, F. Nolting, J. Schurr, and U. Straumann, "Reflections on a Measurement of the Gravitational Constant Using a Beam Balance and 13 Tons of Mercury," arXiv Preprint Server, July, 19, 2014.
- Ephraim Fischbach, Daniel Sudarsky, Aaron Szafer, Carrick Talmadge, and S. H. Aronson, "Reanalysis of the Eötvös experiment," Phys. Rev. Lett., vol. 56, no. no. 1 (January 6, 1986), pp.3-6.
Permanent Link to this article
Linked Keywords: Geek; motif; phenomenon; Henry Cavendish (1731-1810); British; scientist; century; technology; technical; shyness; shy; woman; women; female; domestic worker; servant; Wikipedia; house; housekeeper; Wikimedia Commons; hydrogen; dissolution; dissolve; metal; acid; iron; Fe; hydrogen chloride; HCl; iron chloride; FeCl2; hydrogen; H2; carbonate; carbon dioxide; atmosphere of Earth; air; oxygen; nitrogen; experiment; William Ramsay; John William Strutt, 3rd Baron Rayleigh; Lord Rayleigh; argon; chemistry; physics; electricity; scientific literature; publish; James Clerk Maxwell; Cavendish Professor of Physics; University of Cambridge; Cambridge University; research; Cavendish experiment; density; Earth; gravitational constant; Isaac Newton; law of universal gravitation; force; mass; data; CODATA; meter; kilogram; second; laboratory equipment; apparatus; serendipity; serendipitous; temperature; convection; air current; schematic diagram; sphere; casting; cast; lead; pound mass; torsion; wire; newton; mechanical resonance; resonant frequency; torsion balance; torsion coefficient; physical constant; fundamental constant; precision; parts per million; one-sigma; confidence interval; Committee on Data for Science and Technology; University of Zürich; arXiv; scientist; decade; fifth force; liter; stainless steel; kilogram; liquid; mercury; homogeneity; g/cc; gold plating; gold-plated; electrical conductivity; oxygen-free copper; OFHC; copper; magnetic field; magnetic; measurement uncertainty; relative standard uncertainty.