| Tikalon Blog is now in archive mode.
An easily printed and saved version of this article, and a link
to a directory of all articles, can be found below: |
|
This article |
| Directory of all articles |
Modeling Cities
July 26, 2013
One of the most interesting things about
mathematical modeling is that it can be applied not just to
gas molecules in a container, but to most
systems. This includes
biological systems, such as the
predator-prey interaction modeled by the
Lotka–Volterra equation; and it also includes the behavior of
human populations. Its influence goes beyond the
"hard" sciences into the
social science disciplines of
economics, which is perhaps just semi-soft,
sociology,
psychology and
political science.
One current example in the political science area comes from the
2012 US presidential election, in which
incumbent president,
Barack Obama defeated his
Republican opponent,
Mitt Romney. It's reported that Obama's re-election team relied heavily on computer modeling as a means to
allocate resources.[1-2]
In the weeks prior to the November, 2012, election, Obama analysts used polling data to run 66,000
simulated elections every day.[1-2] This is what I often do, myself, in
Monte Carlo simulations, and I suspect that the actual number was
65,535, which is the limiting value of an
unsigned integer in most
computer languages.
Such simulations were required because of the quirky nature of the US election process. The winner is determined not by the
national popular vote, but by the popular vote in each
state,
weighted by a factor roughly equivalent to the state's population (its number of
Representatives in the
House of Representatives), plus a constant (two
Senators from each state). The full story can be found by looking at the composition of the
US Electoral College.
Urban planning is one area in which mathematical modeling has become important, since the world's populations have been steadily leaving the
countryside to participate in
industries located in larger
cities. The figure below, created from data collected by the
United Nations, shows that in 2005 more than half of the world's population lived in urban areas, as defined by their respective
countries.[3]
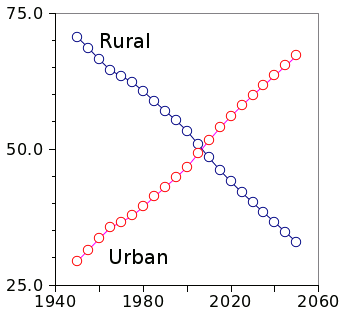
The lure of the big city.
Percentage of people living worldwide in urban and rural areas between 1950 and 2050 (projected).
Unless there are advances in farming technique, and hydroponic factories within cities, we may be headed for a food crisis.[4]
(United Nations Data.)[3]
Six years ago I wrote an article summarizing a study, published in the
Proceedings of the National Academy of Sciences,[5] on
quality of life issues relating to increased
urbanization (
Speed Dating, May 30, 2007). This study found that some
metrics of urban life, such as
wealth and
R&D jobs, increase
exponentially with population. However, most
infrastructure metrics, such as
fuel consumption and
road surface area, have an exponential
decline, which might reflect
economies of scale.
Here's a list of some of the exponents from that study.[5] All items, except the last two from
Germany, are from US
statistics. Hopefully, the
AIDS exponent has decreased in the last six years.
Two recent papers on
arXiv have used
mathematics to model the
population dynamics of cities.[6-7] One of these looks at the difference between urban
mobility and the known trends for long distance travel. Just as in the example that many qualities of city life are exponentially related to population, it was found that that trip length is exponentially distributed.[6]
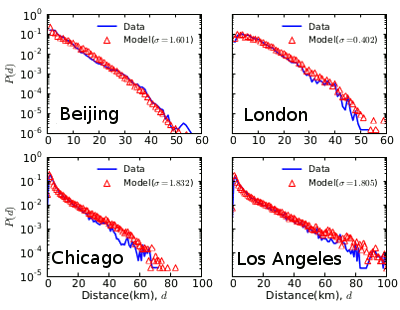
Distribution of trip distance for four major cities.
Data are in blue, and the model is shown in red.
(Fig. 3 of ref. 6, modified for clarity, via arXiv.)[6]
The reason for this is quite understandable. People will go to another place only if there's "something there," be it a unique
store or another
family member.
Population density around cities tends to taper as an exponential of distance from the city center, and trip length and the population density have the same exponential decay rate.[6]
The second paper looks at the
time evolution of
urban sprawl using a 111
year dataset of 45 million people distributed among 8,000 population centers in
Spain.[7] In a process much like
Ostwald ripening, larger cities grow at the expense of smaller cities. In this case, there's an
inertial factor of about fifteen years (no one really likes to move), and a characteristic distance of 70
kilometers. Proximity is the main factor linking the fates of city populations, correlating at 60%.[7]
Evolution of a thousand cities after a hundred years..
These virtual cities, placed randomly in a 500 kilometer square, had the same initial population. The size of the circle indicates the population after 100 years.
(Fig. 3a of ref. 7, via arXiv.)[7]
![]()
References:
- Michael Scherer, "Inside the Secret World of the Data Crunchers Who Helped Obama Win," Time, November 7, 2012.
- Sam Biddle, "Obama's Campaign Ran Millions of Virtual Elections to Predict the Future," Gizmodo, November 7, 2012.
- Population Division of the Department of Economic and Social Affairs of the United Nations Secretariat, World Population Prospects: The 2010 Revision and World Urbanization Prospects: The 2011 Revision.
- Special Report: The Age of Plenty, IEEE Spectrum, 2013.
- Lués M. A. Bettencourt, José Lobo, Dirk Helbing, Christian Kühnert, and Geoffrey B. West, "Growth, innovation, scaling, and the pace of life in cities," Proc. Natl. Acad. Sci. vol. 104, no. 17 (April 24, 2007), pp. 7301-7306.
- Xiao Liang, Jichang Zhao, Li Dong and Ke Xu, "Unraveling the origin of exponential law in intra-urban human mobility," arXiv Preprint Server, May 28, 2013.
- A. Hernando, R. Hernando and A. Plastino, "Space-time correlations in urban sprawl," arXiv Preprint Server, June 16, 2013.
Permanent Link to this article
Linked Keywords: Mathematical model; mathematical modeling; gas; molecule; system; biology; biological; predator-prey; Lotka–Volterra equation; world population; human population; hard science; social science; economics; sociology; psychology; political science; 2012 US presidential election; incumbent; president; Barack Obama; Republican; Mitt Romney; resource allocation; simulation; simulated; Monte Carlo method; Monte Carlo simulation; 65,535; unsigned integer; computer language; national popular vote; state; weight function; weighted; Representative; House of Representatives; Senator; US Electoral College; urban planning; countryside; industry; city; cities; United Nations; country; urban area; rural area; agriculture; farming; hydroponics; hydroponic; famine; food crisis; Proceedings of the National Academy of Sciences of the United States of America; quality of life; urbanization; metric; wealth; research and development; R&D; exponential function; infrastructure; fuel; road; surface area; economies of scale; Germany; statistics; HIV/AIDS; patent; inventor; creativity; wage; bank deposit; crime; electrical cable; arXiv; mathematics; population dynamics; mobility; retail store; family member; Population density; time evolution; urban sprawl; year; Spain; Ostwald ripening; inertia; inertial; kilometer.