The Pizza Race Problem
January 9, 2013
One way to get
children interested in
mathematics is to offer them a treat, such as a
pie or
cake, and have them divide it into fair portions by themselves. If there are just two children, the task can be reduced from a mathematical to a
political task. One child cuts, and the other child chooses which half he or she prefers. When there are three children involved, an impromptu lesson in
trigonometry emerges in which 120
angular degrees and the definition of the
center are the objects of concern.
What happens when an object has already been cut into irregular portions, and the diners need to successively take portions? How much of a quantity advantage could one diner have over the others in this sort of game? Also, what happens when a portion of the object has been previously removed; for example, one slice taken from a
pizza.

My family finds it difficult to understand why I eat pizza with a knife and fork.
Modified Wikimedia Commons image.)
Sharing an irregularly cut pizza is the question posed in the Pizza Race Problem, an analysis of which was posted by Keyue Gao on
arXiv.[1] Gao participated in the
New York University Summer Undergraduate Research Experience(SURE) Program.
Gao's problem is a variation of a problem first posed by
mathematician,
Peter M. Winkler, at a 2008 conference in Budapest in honor of
Laszlo Lovasz's sixtieth
birthday. In the original problem posed by Winkler,
Bob and Alice share a pizza, possibly at a
cryptography conference. The pizza is irregularly sliced by any number of cuts from the center to the edge. Bob and Alice, being proper mathematicians, have decided to eat this pizza according to the following
algorithm:
(1) They choose pieces in an alternating fashion;
(2) Alice starts the meal by selecting any piece of the pizza;
(3) After Alice's first selection, and all subsequent selections, it's only proper to choose one of the pieces adjacent to the empty space.
On each turn, except the first and the last, the diner has a choice of two available pieces. Alice, in selecting first, would take the largest slice, and she would seem to always have an advantage. This is true for an even number of pieces. In that case, Alice, if she chooses wisely, will always get more than half the pizza.
What's interesting is that Alice can actually come away with less than half in the odd piece case. Although Alice gets both the first and last piece in an odd piece pizza, Winkler conjectured she might at a minimum get only
4/9 of the pizza. This conjecture was proven by Kolja Knauer, Piotr Micek and Torsten Ueckerdt.[2]
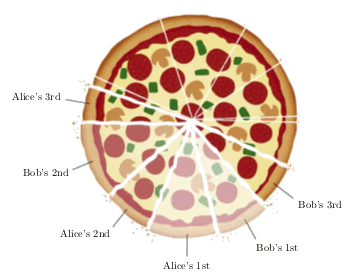
Bob and Alice select pizza pieces.
(Fig. 1 of ref. 2, via the arXiv Preprint Server.)[2)]
Geometrically, the problem reduces to the selection from a
ring of
random numbers adding to 360 degrees. Of course, it doesn't really matter what the numbers add up to, since the sum can be scaled to
2π, or whatever you want. This makes a
computer simulation very easy, since in each case you can just spit out a bunch of random numbers and not worry about their sum.
As is my custom, I've written a simple computer simulation for this pizza problem (
source code,
here). It generates
random pizzas, allows Bob and Alice to make random selections, and it keeps track of the largest portion for Alice. As it turns out, Alice will, on average, do very well in sharing an odd piece pizza, even when she chooses her pieces at random.
Part of this might be because Alice always selects the largest piece as her first piece; and, for some random pies, this piece can be quite a bit larger than others. The following
histogram shows the results of 10,000 trials for an eleven piece pizza in which Alice chooses the largest piece first, and then randomly thereafter.
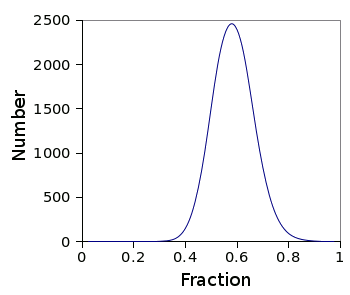
The fraction of pizza that Alice can consume from an eleven piece pizza if she selects the first slice and follows a mathematician's dining etiquette.
(Graph rendered using Gnumeric.)
As can be seen in the histogram, random selection does not always give Alice at least four-ninths (0.444...) of the pizza, but it comes quite close. Just a few percent of the random trials fall below four-ninths (347 out of 10,000, or 3.47%, in one particular simulation run).
Gao adds another
constraint to the problem by requiring Bob or Alice to finish eating their current piece before taking another. In this case, Alice starts first, as before, but the taking of subsequent pieces depends on the size of the pieces currently being eaten. Bob and Alice eat at the same rate. One other constraint is that the sizes of the pieces are such that Alice and Bob will never grab for the same piece at the same time.
This type of sharing would be good for Alice if she's on a diet, since Gao demonstrates that she is only guaranteed two-fifths of the pie. This is just a small variation of the result of the original problem (
0.400 vs 0.444...).[1]
References:
- Keyue Gao, "Pizza Race Problem," arXiv Preprint Server, December 10, 2012
- Kolja Knauer, Piotr Micek and Torsten Ueckerdt, "How to eat 4/9 of a pizza," arXiv Preprint Server, January 24, 2011.
Permanent Link to this article
Linked Keywords: Children; mathematics; pie; cake; politics; political; trigonometry; angular degree; center; pizza; family; knife; fork; Wikimedia Commons; arXiv; New York University; mathematician; Peter M. Winkler; Laszlo Lovasz; birthday; Bob and Alice; cryptography; algorithm; geometry; geometrical; circular buffer; ring; random number; computer simulation; source code; pizza.c; randomness; random; histogram; etiquette; Gnumeric; constraint; Keyue Gao; Pizza Race Problem.