| Tikalon Blog is now in archive mode.
An easily printed and saved version of this article, and a link
to a directory of all articles, can be found below: |
|
This article |
| Directory of all articles |
Lunar Mascons
June 26, 2013
When initially addressing a problem, I usually start with a
spherical cow approximation. Extreme
accuracy is not needed in every investigation, and the extra work to achieve exquisite control in an
experiment would just waste time. When things look promising, I clean things up later. Of course, I always risk overlooking that
Nobel Prize discovery lurking in the next
decimal place,[1] but I'm usually not that lucky.
I remember my first introduction to
significant digits, which was in
high school chemistry. There's always a lot of
long division in chemistry problems, and division was a lot of work in those days before
inexpensive calculators. Knowing when to stop
calculating was a big help. In my
college days,
sliderule calculations were liberating, since your significant digits were physically limited by your computing device.
Mid-twentieth century computing device - The sliderule. The more expensive models were crafted from bamboo. Mid-priced units were aluminum, surprisingly priced the same as their aluminium counterparts. Most students had plastic versions, such as the one pictured. (Photograph by Roger McLassus, via Wikimedia Commons.)
We usually treat the
Earth's mass as a uniform
sphere; and, thereby, a
point source of
gravity at its
center. However, looking out nearly any
window will convince you that
Earth's topography is not that uniform. Of course, Earth's surface features, which range from
Mount Everest (8,848 meters above sea level) to the
Mariana Trench (10,911 meters below sea level), are just 0.31% of the
radius of the Earth (6,371 km); so, it might as well be a perfect sphere. I wrote about Newton's conclusion that a uniform spherical mass can be analyzed as a point mass in a
previous article (Newton's Gravitational Theorem, March 5, 2012).[2]
Aside from these minor surface imperfections, the rest of the Earth is relatively
homogeneous, at least when examined
radially. As the figure shows, the variation of
gravitational acceleration from place to place is of the order of tens of
milliGals, compared with the
standard surface gravity of 976-983 Gal. The overall variation is just 0.01%. The Gal unit is named in honor of
Galileo for his pioneering studies on gravitational acceleration.
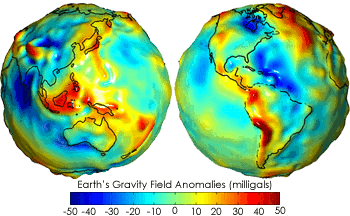
Earth's gravitational anomalies.
The mean gravitational acceleration of the Earth is about 980 Gal, so the anomalies are small.
(NASA image.)
Such uniformity arises from
Earth's large liquid core, which smooths out
mass variation. The situation is somewhat different for the
Moon, which is mostly solid throughout, and it has had frequent encounters with huge
asteroids, as its pock-marked surface shows.
Scientists involved with
NASA's GRAIL mission to map the Moon's gravitational field have just published their findings in
Science.[3-7]
The large gravitational anomalies of the Moon were discovered by scientists from the
Jet Propulsion Laboratory (JPL) just a year before the first manned landing, that of
Apollo 11, on July 20, 1969.[4-5,7]. Excess gravity arises from excess mass, so the source of the anomalies were called "
mascons," short for mass concentrations, but their origin was unclear. The surprising finding was that the mascons were located in the
lunar basins (lunar maria), the regions in which mass should be deficient. Possible reasons were
iron-rich
lava filling the areas, or large concentrations of mass just below the surface.[4,6]
The GRAIL lunar gravity mapping was done by a team with members from five
US universities, one
French university, NASA's
Goddard Space Flight Center, and two
research institutes.
Maria Zuber, a
Professor of
Geophysics in the
MIT Department of Earth, Atmospheric and Planetary Sciences and MIT's vice president for research, is GRAIL's
principal investigator.
Jay Melosh, Distinguished Professor in
Purdue University's Department of Earth, Atmospheric, and Planetary Sciences, was the lead author of the Science paper.
This mapping was done using
microwave range data between two
spacecraft,
GRAIL A and GRAIL B, renamed Ebb and Flow. These craft were placed in a nearly
circular orbit passing over the
poles of the Moon at low
altitude (about 34
miles, or 55
kilometers). As these craft passed over areas of greater and lesser gravity, their separation changed slightly.[4-5] Such range data allowed a determination of the local lunar gravity over the entire lunar sphere, as seen in the figure.
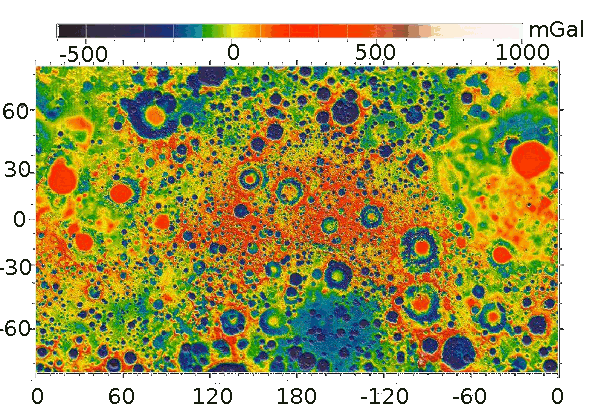
The gravity field of the Moon, as determined by GRAIL. The map is a Mercator projection. (NASA/JPL-Caltech/GSFC/MIT image.)
As can be seen in the map, the mascons look like
target patterns with a gravity excess in the center surrounded by a gravity deficit. In many cases, there's a positive outer
annulus. This pattern arises from the the process of mascon creation, which starts with
crater excavation, collapse of the impact area, and the
isostatic adjustment, cooling and contraction of the melted material.[3-5] The asteroid impact doesn't just eject material. It also sends a
shock wave into the Moon's interior that brings up
dense lunar
mantle material to the surface.[6]
Jay Melosh's part of the investigation was to
model the process by
hydrocodes and
finite element analysis. The Purdue team analyzed the
Freundlich-Sharonov and
Humorum mascon basins, and the simulations precisely matched the gravity observations.[5-6]
Says MIT's Maria Zuber,
"Mascons also have been identified in association with impact basins on Mars and Mercury... Understanding them on the moon tells us how the largest impacts modified early planetary crusts."[4]
References:
- In 1894, Albert A. Michelson of the eponymous Michelson-Morley experiment attributed the following to William Thomson (Lord Kelvin). "An eminent physicist remarked that the future truths of physical science are to be looked for in the sixth place of decimals."
- Isaac Newton, "Principia: The Mathematical Principles Of Natural Philosophy," English translation, via Archive.org. The theorem is found as Proposition LXXI, Theorem XXXI.
- H. J. Melosh, Andrew M. Freed, Brandon C. Johnson, David M. Blair, Jeffrey C. Andrews-Hanna, Gregory A. Neumann, Roger J. Phillips, David E. Smith, Sean C. Solomon, Mark A. Wieczorek and Maria T. Zuber, "The Origin of Lunar Mascon Basins," Science, Published Online May 30, 2013, DOI: 10.1126/science.1235768.
- NASA's GRAIL Mission Solves Mystery of Moon's Surface Gravity, NASA Press Release, May 30, 2013.
- Elizabeth Gardner, "Purdue-led team solves one of the moon's mysteries," Purdue University Press Release, May 30, 2013.
- Jennifer Chu, "An answer to a lunar mystery: Why is the moon's gravity so uneven?" MIT Press Release, May 30, 2013.
- Michael Lemonick, "Revealed: The Awesome Explanation for the Moon's Extra Gravity," Time, May 30, 2013.
Permanent Link to this article
Linked Keywords: Spherical cow; approximation; accuracy; experiment; Nobel Prize; decimal place; significant digits; high school; chemistry; long division; inexpensive calculator; calculation; calculatingvcollege; slide rule; sliderule; bamboo; aluminum; aluminium; plastic; Wikimedia Commons; Earth's mass; sphere; point source; gravitation; gravity; center; window; Earth; topography; Mount Everest; Mariana Trench; radius of the Earth; homogeneous; radius; radial; gravitational acceleration; milliGal; standard surface gravity; Galileo Galilei; gravity anomaly; gravitational anomaly; Earth's large liquid core; mass; Moon; asteroid; scientist; NASA; Gravity Recovery and Interior Laboratory; GRAIL mission; Science; Jet Propulsion Laboratory; Apollo 11; mascon; lunar mare; lunar basin; iron; lava; United States; US; university; France; Goddard Space Flight Center; research institute; Maria Zuber; Professor; Geophysics; Massachusetts Institute of Technology; MIT; Department of Earth, Atmospheric and Planetary Sciences; principal investigator; Jay Melosh; Purdue University; Department of Earth, Atmospheric, and Planetary Sciences; microwave; range data; spacecraft; GRAIL A and GRAIL B; circular orbit; pole; altitude; mile; kilometer; Mercator projection; target pattern; annulus; impact crater; isostasy; isostatic; shock wave; density; dense; mantle; computer simulation; computer model; fluid dynamics; hydrocode; finite element method; finite element analysis; Freundlich-Sharonov; Humorum; Mars; Mercury; planet; planetary; crust; William Thomson; Lord Kelvin; Isaac Newton, "Principia: The Mathematical Principles Of Natural Philosophy."