Light Speed
April 8, 2013
Eyeglasses are only possible because of
refraction, the bending of
light rays when they enter a medium at an
angle. The refraction of a
material is measured by its
refractive index n, which is simply the ratio of the
speed of light in a
vacuum c to the speed of light in the medium
v; that is,
n =
c/
v.
Optics was the topic of the first chapter of my
high school PSSC physics textbook. That may have been because optics is easy to visualize (pun intended). This bending of light rays into a medium and its relationship to the speed of propagation of a
wavefront was explained in that book using an
analogy of
marching soldiers.
The front tier of marching soldiers enters a
muddy field at an angle. At first, a single soldier at one end finds the marching somewhat difficult, and he slows down. To prevent the soldier at his back from bumping against him, he veers to one side. This continues, until we see the
parade refraction in the figure below.

A parade of soldiers being refracted at the interface between grass and a muddy field
The difficulty with most analogies is that they explains things in one sense, but they lack explanatory benefit at a deeper level.
I wasn't comfortable with this analogy in high school.
(Source image for soldier icon via Wikimedia Commons, modified.)
This behavior of light rays was quantified by
Dutch astronomer and
mathematician,
Willebrord Snellius (1580-1626), as
Snell's law (see figure). As was the custom of his time, Snellius
Latinized his birth name, Willebrord Snel van Royen. Snell's law follows from
Fermat's principle of least time. In
mechanics, the equivalent of this principle is the
principle of least action, in which we're reminded that
Nature also enjoys doing things the easy way.

Snell's Law
In most cases, the top medium is air, which has a refractive index of 1.000
The ratio of refractive indices is related to the ratio of the speed of light in the media, (n1/n2 = v2/v1)
According to Wikipedia, there's evidence that this law was first formulated by the Persian scientist, Ibn Sahl, six centuries before Snellius.
(Illustration by the author using Inkscape.)
One interesting thing about Snell's law is that there's an angle,
θ = arcsin(n2/n1), beyond which no light is transmitted from one medium to the other. It's completely
reflected, a condition called
total internal reflection. This property is useful, since it allows
prisms to reflect light without any reflective
metal coating (usually
aluminum). It also allows an important way to couple light into
liquid droplets in some
sensors.
The following table lists some
representative values of refractive index at
visible wavelengths.
The refractive index of materials varies with
wavelength, becoming smaller as the wavelength increases. This change in index is very predictable, and the refractive index over a range of wavelengths can be calculated from the
Sellmeier equation if the index at just a few wavelengths is known. This equation is usually written as
n2(λ) = 1 + [B1 λ2/(λ2 - C1)] + [B2 λ2/(λ2 - C2)]
+ [B3 λ2/(λ2 - C3)]
For fused silica, B
1 = 0.696166300, B
2 = 0.407942600, B
3 = 0.897479400, C
1 = 4.67914826×10
−3 μm
2, C
2 = 1.35120631×10
−2 μm
2, and C
3 = 97.9340025 μm
2.
I worked for several years with an
optical physicist who was tasked with making accurate thickness measurements for thin
crystal films I prepared in my
laboratory. Not a day would pass when he didn't mention the Sellmeier equation.
That was the time when
general purpose computers were just being integrated into laboratories, and he had an
automated system for film thickness measurement based on
optical interference. Accurate refractive index values over a wide range of wavelengths were needed for his calculations. The utility of the Sellmeier equation can be seen in the following figure.
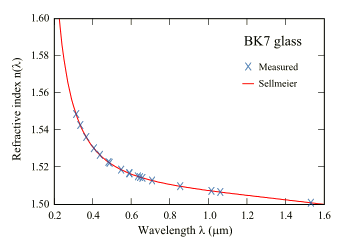
The refractive index of BK7 glass over a wide range of wavelengths, and the Sellmeier equation fit to the data.
The agreement is excellent.
(Wikipedia image by Bob Mellish.)
Refractive indices are referenced to the vacuum. As I've written in the context of the
Casimir effect (
Not So Empty Space, July 23, 2008 ) the vacuum is not really empty space. Empty space is only empty when averaged over a period of time. At any instant, it's a sea of
virtual particles coming into and out of existence. Physicists are now considering the possibility that the speed of light we measure is an average value. It will show variation over very short length scales.[1-7]
Physicists from the
Université Paris-Sud (Orsay, France), the
Université Paris Diderot (Paris, France), the
Max-Planck-Institut für die Physik des Lichts (Erlangen, Germany), the
Universität Erlangen-Nürnberg (Erlangen, Germany) and the
Universidad Complutense (Madrid, Spain) have published two papers in the
European Physical Journal about this concept.[2,4]
One paper shows the possibility that the
vacuum permeability,
μo, a
magnetic constant, and the
vacuum permittivity,
εo, an
electrical constant, may arise from the
polarization and
magnetization of continuously appearing and disappearing
fermion pairs of the virtual particle sea.[2,3] Light, which is an
electromagnetic wave, would interact with these particles in a granular fashion at the
Planck scale, so its speed would vary. All such interactions average out at larger length scales to give us the speed of light we measure.[2,3] The time scale for such fluctuation is estimated to be about 50
attoseconds, so an
experimental test might soon be possible.[1]
The other paper uses this idea to estimate the total number of
charged elementary particles in nature. They calculate that the
vacuum impedance arises from the charges of the virtual particles, and they predict that the total number of charged elementary particles is about a hundred.[1,4-5]
References:
- Ephemeral vacuum particles induce speed-of-light fluctuations, Springer Press Release, March 25, 2013.
- Marcel Urban, Francois Couchot, Xavier Sarazin and Arache Djannati-Atai, "The quantum vacuum as the origin of the speed of light," European Physical Journal D, vol. 67, no. 58 (March 21, 2013), DOI 10.1140/epjd/e2013-30578-7.
- Marcel Urban, Francois Couchot, Xavier Sarazin and Arache Djannati-Atai, "The quantum vacuum as the origin of the speed of light," arXiv Preprint Server, February 21, 2013.
- Gerd Leuchs and Luis L. S´nchez-Soto (2013), "A sum rule for charged elementary particles," European Physical Journal D, vol. 67, no. 57 (March 21, 2013), DOI 10.1140/epjd/e2013-30577-8.
- Gerd Leuchs and Luis L. Sanchez-Soto, "A sum rule for charged elementary particles," arXiv Preprint Server, January 15, 2013.
- M. Urban, F. Couchot and X. Sarazin, "A mechanism giving a finite value to the speed of light, and some experimental consequences," arXiv Preprint Server, November 8, 2011.
- M. Urban, F. Couchot, X. Sarazin, "Does the speed of light depend upon the vacuum ?" arXiv Preprint Server, June 20, 2011.
Permanent Link to this article
Linked Keywords: Eyeglasses; refraction; light ray; angle; material; refractive index; speed of light; vacuum; optics; high school; Physical Science Study Committee; PSSC; physics; textbook; wavefront; analogy; marching; soldiers; mud; parade; grass; Wikimedia Commons; Dutch; astronomer; mathematician; Willebrord Snellius; Snell's law; Latinize; Fermat; principle of least time; mechanics; principle of least action; Nature; Wikipedia; Iran; Persian; scientist; Ibn Sahl; Inkscape; reflection; total internal reflection; prism; metal; aluminum; liquid droplet; sensor; list of refractive indices; visible spectrum; visible wavelength; Titanium dioxide (Rutile); Borosilicate glass; Pyrex; Diamond; Fused silica (Fused Quartz); Cubic zirconia; atmosphere of Earth; Air; standard conditions for temperature and pressure; STP; Polycarbonate; vacuum; sucrose; sugar; wavelength; Sellmeier equation; optical physicist; crystal; laboratory; general purpose computer; automation; optical interference; Wikipedia; Bob Mellish; Casimir effect; virtual particle; Université Paris-Sud (Orsay, France); Université Paris Diderot (Paris, France); Max-Planck-Institut für die Physik des Lichts (Erlangen, Germany); >Universität Erlangen-Nürnberg (Erlangen, Germany); Universidad Complutense (Madrid, Spain); European Physical Journal; vacuum permeability; magnetism; vacuum permittivity; electricity; electrical; polarization; magnetization; fermion; electromagnetic radiation; electromagnetic wave; Planck scale; attosecond; experiment; experimental test; electric charge; elementary particle; vacuum impedance.