Moona Lisa
January 28, 2013
It must have been exciting to have worked in the
early days of computing, since there were so many fundamental things waiting to be discovered. Here are a few important examples from the
1960s and
1970s.
• The Quicksort Algorithm
• The Fast Fourier Transform
• Lempel-Ziv Compression
• Reed–Solomon Error Correction
The very useful quicksort algorithm was invented by
computer scientist,
C.A.R. (Tony) Hoare, in 1960, while he was a visiting student at
Moscow State University, working on
Russian-to-
English translation software. Hoare invented quicksort as a way to make the computer translation more efficient. The algorithm is now widely used, since it sorts efficiently in
order O(n log n).[1]
The fast Fourier transform (FFT) algorithm was invented by
James Cooley and
John Tukey in 1965 while Cooley was at the
IBM Thomas J. Watson Research Center and Tukey was sharing his time between
Bell Labs and
Princeton University. Cooley and Tukey worked at separate times with
John von Neumann at the
Institute for Advanced Study,
Princeton, New Jersey, where Tukey coined the word, "
bit."

A drawing of an Abraxas Marginata (Lomaspilis marginata) butterfly, via Wikimedia Commons.
An important part of the FFT algorithm is the "butterfly," a diagram that shows how to construct the transform from its parts)
the Cooley-Tukey FFT is a
recursive algorithm that breaks the
Fourier transform into smaller transforms that are calculated separately and combined to obtain the transform.[2] Since so many things
mathematical were anticipated by either
Euler or
Gauss, it's no surprise that it was found that the algorithm was developed by Gauss around 1805 and published after his death.[3-4]
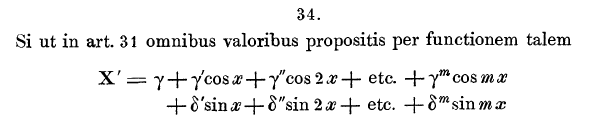
An excerpt from the paper of Carl Friedrich Gauss describing trigonometric transforms relevant to the Fourier transform. (Via Université du Sud-Toulon-Var))
Gauss developed his equations to interpolate the
orbits of the
asteroids,
Pallas and
Juno. As it turns out, Gauss' work predates even
Fourier's publication in 1807, although Fourier would not have known, since Gauss' work was unpublished at the time. Cooley and Tukey extended the results into the computer realm by their analysis of the
asymptotic computational time of their FFT.
Abraham Lempel and
Jacob Ziv invented their lossless data compression algorithm, called
LZ77, in 1977.[5] The Lempel-Ziv algorithm was extended by
Terry Welch in 1984 to form
Lempel–Ziv–Welch (LZW) compression, which was very important in the early history of the
Internet when
channel capacities were limited. The
IEEE declared these algorithms an
IEEE Milestone in 2004.
Irving S. Reed and
Gustave Solomon invented their eponymous
Reed–Solomon error correction method in 1960. At that time they were able to present an efficient coding algorithm, but not one as efficient for decoding. This was not a major problem, since one of its uses was sending back images and data from the
Voyager spacecraft. Coded signals from the spacecraft could be decoded easily by
mainframes back on Earth.
Reed–Solomon codes are especially suitable for
burst error correction, so they're used for
digital data storage devices, such as
optical discs,
DSL, and some
wireless computer communication. It's not possible in a short article to describe how Reed–Solomon codes work, but Wikipedia has a
very nice page. In reading that, you can be thankful that
mathematicians became interested in
computer science.
An interesting application of Reed–Solomon coding was recently in the news.
NASA transmitted an image of
Leonardo da Vinci's Mona Lisa painting via
laser to its
Lunar Reconnaissance Orbiter in orbit around the
Moon since 2009. The spacecraft received the laser signal with an onboard instrument and transmitted it back to
Earth by
radio. This was a
proof-of-concept experiment demonstrating that laser communication is possible at
near-planetary distances.[6-10]

Reed-Solomon error correction as applied to a laser-transmitted image of the Mona Lisa. The left image shows the raw data, and the right image shows the corrected data. The image was transmitted over a range of nearly a quarter of a million miles from the Earth to Moon orbit. (NASA Goddard image by Xiaoli Sun.)
The Lunar Reconnaissance Orbiter (LRO) has been
topographically mapping the moon from an orbit about 31 miles above its surface and making a
gravitational map, as well. As part of its normal operations, the LRO is tracked form Earth by laser.[7,10] This laser ranging is accomplished with LRO's
Lunar Orbiter Laser Altimeter (LOLA) in combination with the
Next Generation Satellite Laser Ranging station at NASA's
Goddard Space Flight Center,
Greenbelt, Maryland.[7]
NASA scientists were able to add a data stream to this rangefinder without affecting its performance.[7] Says
Xiaoli Sun, leader of the team for this experiment,
"Because LRO is already set up to receive laser signals through the LOLA instrument, we had a unique opportunity to demonstrate one-way laser communication with a distant satellite."[7]
The Mona Lisa image was contained in a 152x200
pixel array of 12 bit
grayscale data. The data were sent using
pulse-position modulation in which the gray value was determined by the position of the laser pulse in a time frame. The data rate was a modest 300
bits per second, but laser communication has a potential for a higher data rate than radio.[7-8,10] The Reed-Solomon coding was used to correct for transmission errors from
turbulence in
Earth's atmosphere.[7]
Why the Mona Lisa? NASA claims it's because the Mona Lisa is an "iconic" image; and also, because people can recognize when it's been altered.[8] Another reason might be because it's in the
public domain in the
United States (and at the Moon?). Now that the concept of
perpetual copyright has been established, it would have been impossible for NASA to have sent an image of
Mickey Mouse without securing special permission.[11]
References:
- C. A. R. Hoare, "Quicksort," Computer Journal, vol. 5, no. 1 (1962), pp. 10-16. PDF file, here.
- J.W. Cooley and J.W. Tukey, "An algorithm for the machine calculation of complex Fourier," Math. Comput., vol. 19 (1965), pp. 297-301. PDF file, here.
- Carl Friedrich Gauss, "Theoria interpolationis methodo nova tractata", Werke, Band 3, Königliche Gesellschaft der Wissenschaften, Göttingen, 1866),pp. 265-327 (5.9 MB PDF File).
- James W. Cooley and John W.Tukey, "On the Origin and Publication of the FFT Paper," Citation Classics, Current Contents, vol. 33, nos. 51-52 (December 20-27, 1993), pp. 8-9.
- J. Ziv and A. Lempel, "A Universal Algorithm for Sequential Data Compression," IEEE Transactions on Information Theory, vol. 23, no. 3 (May, 1977), pp. 337-343.
- Xiaoli Sun, David R. Skillman, Evan D. Hoffman, Dandan Mao, Jan F. McGarry, Leva McIntire, Ronald S. Zellar, Frederic M. Davidson, Wai H. Fong, Michael A. Krainak, Gregory A. Neumann, Maria T. Zuber and David E. Smith, "Free space laser communication experiments from Earth to the Lunar Reconnaissance Orbiter in lunar orbit," Optics Express, vol. 21, no. 2, (2013), pp. 1865-1871.
- Nancy Neal-Jones and Elizabeth Zubritsky, "NASA Beams Mona Lisa to Lunar Reconnaissance Orbiter at the Moon," NASA Goddard Press release No. 13-003, January 17, 2013
- Matthew Shaer, "Mona Lisa rides laser beams all the way to the moon: NASA," Christian Science Monitor, January 18, 2013.
- Alex Knapp, "NASA Uses Lasers To Send The Mona Lisa To The Moon," Forbes, January 18, 2013.
- Megan Garber, "We Just Sent the Mona Lisa to the Moon ... With Lasers," The Atlantic, January 17, 2013.
- Disney forced the removal of murals featuring their cartoon figures from the walls of three Florida day care centers, as discussed in this Snopes.com article.
Permanent Link to this article
Linked Keywords: History of computing hardware; early days of computing; 1960s; 1970s; Quicksort Algorithm; Fast Fourier Transform; Lempel-Ziv Compression; Reed–Solomon Error Correction; computer scientist; C.A.R. (Tony) Hoare; Moscow State University; Russian; English; translation; software; analysis of algorithms; order O(n log n); James Cooley; John Tukey; IBM Thomas J. Watson Research Center; Bell Labs; Princeton University; John von Neumann; Institute for Advanced Study; Princeton, New Jersey; bit; Abraxas Marginata (Lomaspilis marginata) butterfly; Wikimedia Commons; butterfly; recursion; recursive algorithm; Fourier transform; mathematics; mathematical; Leonhard Euler; Carl Friedrich Gauss; trigonometry; trigonometric; Theoria interpolationis methodo nova tractata; Université du Sud-Toulon-Var; orbit; asteroid; Pallas; Juno; Joseph Fourier; asymptotic computational complexity; asymptotic computational time; Abraham Lempel; Jacob Ziv; LZ77; Terry Welch; Lempel–Ziv–Welch; Internet; channel capacity; Institute of Electrical and Electronics Engineers; IEEE; IEEE Milestone; Irving S. Reed; Gustave Solomon; Reed–Solomon error correction method; Voyager spacecraft; mainframe computer; burst error; data storage device; optical disc; digital subscriber line; DSL; wireless LAN; wireless computer communication; mathematician; computer science; NASA; Leonardo da Vinci; Mona Lisa painting; laser; Lunar Reconnaissance Orbiter; Moon; Earth; radio; proof-of-concept; experiment; planetary; Xiaoli Sun; topographic map; topographically mapping; gravitation; gravitational; Lunar Orbiter Laser Altimeter (LOLA); Next Generation Satellite Laser Ranging station; Goddard Space Flight Center; Greenbelt, Maryland; pixel; grayscale; pulse-position modulation; bits per second; turbulence; Earth's atmosphere; public domain; United States; Copyright Term Extension Act; perpetual copyright; Mickey Mouse.