"Leonardo's" Proof of the Pythagorean Theorem
December 2, 2013
Pythagoras (Πυθαγορας), more properly called Pythagoras of
Samos, lived in the estimated period from 570
BC - 495 BC. Not much is known about Pythagoras, since he flourished in the dim times of
Pre-Socratic philosophy. He was a
philosopher and the founder of a
religious movement, but he is best known as a
mathematician and supposed author of the
Pythagorean theorem.

Pythogoras thought that the "unreasonable effectiveness of mathematics in the natural sciences"[1] was a consequence of numbers being the true nature of things.
Two quotations attributed to Pythagoras are "Mathematics is the way to understand the universe," and "Number is the measure of all things."[2]
(Via Wikimedia Commons.)
While the
early Greeks thought that the rising and setting
Venus were two different
planets,
Phosphorus and
Hesperus, Pythagoras is said to have identified these as the single planet.[3]
As most of the
Pre-Socratic philosophers, Pythagoras followed in the tradition of
Thales, who rejected the idea that things happened according to the will of the
gods and looked, instead, for a
scientific explanation of
natural phenomena. More importantly, Thales was a
geometer, and he is the first known to have used
deduction in
geometry. He is famous for
Thales' theorem, that any
angle inscribed in a
semicircle is a
right angle.
I wrote about the Pythagorean theorem in two previous articles (
Martin Gardner May 31, 2010 and
Presidents of Purpose, February 20, 2012. Aside from the proof of this theorem attributed to Pythagoras, there are more than 370 other proofs,[4] which makes the greatest obstacle to creating an original proof the knowledge of all the others. My favorite, perhaps because of its simple
construction, is shown below. It's credited to the
12th century Hindu mathematician,
Bhaskara (1114-1185).
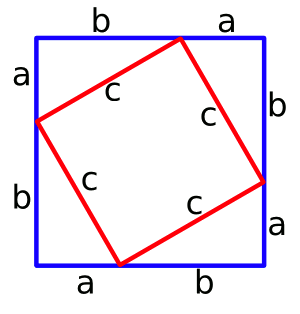
Construction to prove the Pythagorean theorem.
The area of the inner square is c2, the area of the outer square is (a+b)2, and the area of each triangle is (1/2)(ab).
Knowledge of the areas, and a little math, gives the theorem.
(Drawing by the author using Inkscape.)
Creating novel proofs of the Pythagorean theorem was a common
intellectual pursuit.
James Garfield (1831-1881), the twentieth
U.S. President discovered a novel proof of the Pythagorean theorem when he was a member of the
U.S. House of Representatives. The construction of his proof is shown in the figure, from which the obvious solution
can be derived by equating the area of the
trapezoid to that of the
triangles.
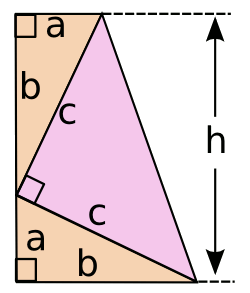
US President James Garfield's proof of the Pythagorean theorem.
The proof is made by equating the area of the trapezoid to the combined area of the triangles.
Although a high school student should be able to complete the proof when given this construction, you can find the solution here.
Inkscape illustration by the author)
The
Renaissance artist,
Leonardo da Vinci (1452-1519), is known also for his many
inventions, all of which were rendered as
drawings by his expert hand. Leonardo and his
colleague artists had a professional interest in some aspects of geometry, such as
perspective, but Leonardo seemed to have an interest in advanced mathematics as well.
Leonardo's interest in geometry can be seen in his 1492 drawing of the
Vitruvian Man, that well known image of a man inside a circle and square. Leonardo studied mathematics under the
Franciscan monk,
Luca Pacioli, and he illustrated Pacioli's 1497 book (published in 1509), "
De divina proportione," about artistic and
mathematical proportions.
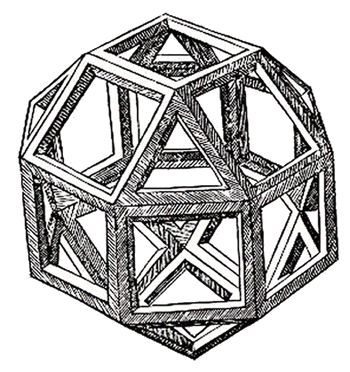
Leonardo's drawing of a rhombicuboctahedron, an Archimedean solid formed from squares and triangles.
(Woodcut from Pacioli's De divina proportione (Venice, 1509).Via Wikimedia Commons.)
For these reasons, it's credible that a proof of the Pythagorean theorem ascribed to Leonardo was actually invented by him. The construction for "Leonardo's proof" is shown in the figure. Given the construction, the proof is easy, but you can find the proof in ref. 5.[5]
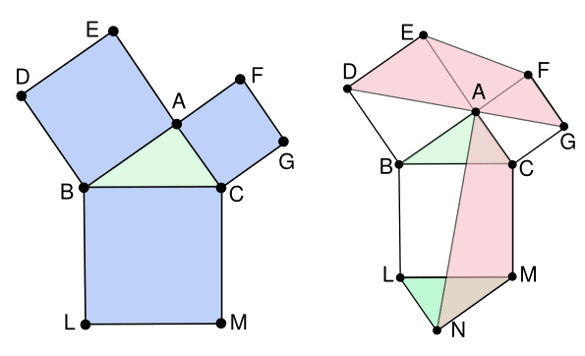
Geometrical construction for "Leonardo's" proof of the Pythagorean theorem. (Drawn by the author using Inkscape.)
Some
bibliographic scholarship by
Franz Lemmermeyer of
St. Gertrudis school in
Ellwangen shows that Leonardo da Vinci's proof of the Pythagorean theorem was actually authored in 1772 by
German physicist Johannes Tobias Mayer (1752-1830).[6] Mayer lectured, also, on mathematics at the
Georg-August University of Göttingen.
References:
- Eugene P. Wigner, "The unreasonable effectiveness of mathematics in the natural sciences," Communications on Pure and Applied Mathematics, vol. 13, no. 1 (February 1960), doi:10.1002/cpa.3160130102, pp. 1-14. PDF file available, here.
- R. W. Hamming, "The Unreasonable Effectiveness of Mathematics," The American Mathematical Monthly, vol. 87, no. 2 (February, 1980), via the Center for Cancer Research Nanobiology Program.
- John D. Page, "Pythagoras," Math Open Reference Web Site.
- Elisha Scott Loomis, "The Pythagorean proposition: its demonstrations analyzed and classified, and bibliography of sources for data of the four kinds of proofs," Education Resources Information Center. Institute of Education Sciences (IES) of the U.S. Department of Education (1940); reprinted in 1968 by National Council of Teachers of Mathematics (310 page PDF File).
- Stephen Szydlik, "Proving the Pythagorean Theorem, Pythagoras Proof #5," University of Wisconsin Oshkosh Web Site (7 page PDF File).
- Franz Lemmermeyer, "On Leonardo da Vinci's proof of the Theorem of Pythagoras," arXiv Preprint Server, November 4, 2013.
Permanent Link to this article
Linked Keywords: Pythagoras; Samos; Anno Domini; BC; Pre-Socratic philosophy; philosopher; religious movement; mathematician; Pythagorean theorem; The Unreasonable Effectiveness of Mathematics in the Natural Sciences; number; De rerum natura; nature of things; Wikimedia Commons; Ancient Greece; early Greeks; Venus; planet; Phosphorus; Hesperus; Pre-Socratic philosopher; Thales; gods; scientific explanation; natural phenomenon; geometer; deductive reasoning; deduction; geometry; Thales' theorem; inscribed angle; semicircle; right angle; compass-and-straightedge construction; geometrical construction; 12th century; Bhaskara (1114-1185); area; square; triangle; Inkscape; intellectual; James Garfield (1831-1881); President of the United States; United States House of Representatives; trapezoid; triangle; high school; Renaissance; artist; Leonardo da Vinci (1452-1519); science and inventions of Leonardo da Vinci; drawing; collegiality; colleague; perspective; Vitruvian Man; Franciscan monk; Luca Pacioli; De divina proportione; mathematical proportion; rhombicuboctahedron; Archimedean solid; Woodcut; Venice; bibliographic; scholarly method; scholarship; Franz Lemmermeyer; St. Gertrudis school; Ellwangen; German; physicist; Johannes Tobias Mayer (1752-1830; Georg-August University of Göttingen.