| Tikalon Blog is now in archive mode.
An easily printed and saved version of this article, and a link
to a directory of all articles, can be found below: |
|
This article |
| Directory of all articles |
Phyllotaxis
April 4, 2012
Scientists attempt to find order in every aspect of
nature, although they sometimes fool themselves. There's the example of
Bode's Law that I wrote about in a
previous article (Planetary System Formation, March 21, 2012). Bode's Law (sometimes called the Titius-Bode Law) appeared to accurately formulate the distance of the
planets from the
Sun. Although there was no physical basis for the law, it worked very well for the planets of
antiquity. However, it failed miserably when data for
Neptune and
Pluto were added.
The
Fibonacci numbers are a
mathematical sequence whose rule is easily stated. You begin with the numbers 0 and 1; then the subsequent numbers are defined as the sum of the previous two in the sequence. Thus,
0
1
1 = 1 + 0
2 = 1 + 1
3 = 2 + 1
5 = 3 + 2, etc.
The Fibonacci numbers are known as sequence
A000045 in the
On-Line Encyclopedia of Integer Sequences. Such a low catalog number might be indicative of a special place in mathematics, although sequence
A000004, which is all zeros, might be used as a
counterexample.
The reason that the Fibonacci numbers are interesting to scientists is that certain things in nature appear to conform to this sequence. One idealized example is the number of pairs of
rabbits in each
generation, as shown in the figure. In practice, however, it's unlikely that rabbit populations would evolve this way.
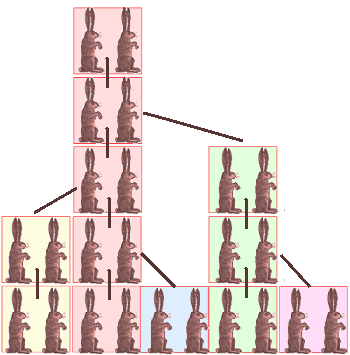
Fibonacci Rabbits
If a male-female pair of rabbits reaches sexual maturity in one generation and subsequently has one male and one female progeny in each generation, the number of pairs of rabbits in each generation will follow the Fibonacci sequence if all rabbits remain alive.
(Illustration by author. Original rabbit image from Wikimedia Commons)
The Fibonacci sequence seems to occur in the
spiral pattern of
seeds in a
sunflower and the number of
petals in a
flower. Most
daisies have 34, 55, or 89 petals, all Fibonacci numbers, and it's been suggested that the reason for the rarity of
four-leaf clovers is because four isn't a Fibonacci number. Since the arrangement of
leaves on a
plant stem is called
phyllotaxis, this term has been used to describe the arrangement of any element of the plant, such as the seeds and petals.
Something this general must have an explanation, and the concept was of interest to
Alan Turing, who also wrote an article about how the
leopard gets its
spots.[1] Last year, the
American Association for the Advancement of Science (AAAS) held a session on "Growth and Form in Mathematics,
Physics, and
Biology," during its annual meeting.[2] This session was a commemoration of the 150th anniversary of the birth of
mathematical biologist,
D'Arcy Thompson.
Alan Newell of the
University of Arizona (not to be confused with another
Allen Newell known to many
computer scientists) has proposed a physical explanation for this occurrence of the Fibonacci sequence in nature. This work was described in a paper presented at that AAAS session, and in previous publications[3-8]. The explanation is based on the
mechanics of materials.
Galileo was one of the first to propose that the size and shape of
organisms is governed by mechanics. Galileo's
square-cube law, stated in his
Two New Sciences (1638), is the observation that as the size of an object increases, the
volume grows at a faster rate than its
surface area. More importantly, in mechanics, the volume of a body grows faster than the
cross-sectional area of members that support the body against
gravity. A
giant can't have
human-style feet. It would need
elephant-like feet.
D'Arcy Thompson elaborated on the idea that organisms must still obey the laws of physics in his 1917 book, "
On Growth and Form." This book, which contains many examples of phyllotaxis, is more descriptive than explanatory, but it does make a connection between physics and biology.
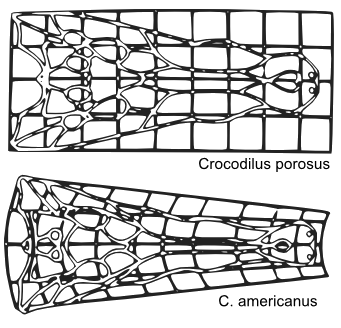
In this portion of an illustration from D'Arcy Thompson's book, a Crocodylus porosus (saltwater crocodile) head can be transformed into an american crocodile (Crocodylus americanus, or Crocodylus acutus) head by a simple geometrical transformation.
(Source image, Wikimedia Commons))
Newell, along with his colleagues and students, has been looking at the stress-relieving affect of
buckling as the cause of the Fibonacci patterns in nature. Buckling drives the development of the patterns, since it affects subsequent growth. The buckling, which causes ridge formation on surfaces, happens when the growth layer intrudes into softer
tissue as a means of reducing
stress.[7]
As we find in nearly every process, the path of least
energy is the one that's taken.[5] Says Newell,
"Of all possible shapes you can have, what nature picked minimizes the energy in the plant." [7]
Such a least-energy path leads to the Fibonacci patterns.[5]
As I've often remarked,
theory is one thing, but you can't beat a good
experiment. It's always been stated that sunflower seeds follow a Fibonacci pattern, but the last experimental test of that, done in 1938 on 319 specimens, was inconclusive.[9] To do an analysis on a larger
sample size, scientists at the
University of Manchester have teamed with the Manchester
Museum of Science and Industry and the
Manchester Science Festival to have people grow more than 3,000 sunflowers for analysis. The results of the analysis will be announced at the festival in October, 2012.[9]
Computer-generated sunflower pattern based on a mathematical model developed at the University of Arizona.
(University of Arizona image by Matt Pennybacker))
![]()
References:
- A. M. Turing, "The Chemical Basis of Morphogenesis," Philosophical Transactions of the Royal Society of London. Series B, Biological Sciences, vol. 237, no. 641. (August 14, 1952), pp. 37-72; PDF file available, here.
- Growth and Form in Mathematics, Physics, and Biology, the American Association for the Advancement of Science Annual Meeting, February 18, 2011.
- Alan Newell, "The Universal Nature of Fibonacci Patterns," Presentation 2903 of the AAAS 2011 Annual Meeting.
- Mari N. Jensen, "How nature's patterns form," University of Arizona Press Release, February 18, 2011.
- Patrick D. Shipman and Alan C. Newell, "Phyllotactic Patterns on Plants," Physical Review Letters, vol. 92, no. 16 (April 23, 2004), Document No. 168102.
- Erica Klarreich, "Cactus Patterns Buckle Up," Physical Review Focus, April 6, 2004.
- Kara Rogers, "UA Mathematicians Predict Patterns in Fingerprints, Cacti," Fractal.org, March 31, 2004.
- Alan Newell, "A conversation on nature's patterns," Video of a talk at the University of Arizona Department of Mathematics, December 14 2010.
- Ruth Hazard, "Thousands of sunflowers to be planted in honour of Alan Turing for MOSI-led experiment," Culture24.org, March 23, 2012.
Permanent Link to this article
Linked Keywords: Scientist; nature; Bode's Law; planet; Sun; antiquity; Neptune; Pluto; Fibonacci number; mathematics; Sloan A000045; On-Line Encyclopedia of Integer Sequences; Sloan A000004; counterexample; rabbit; generation; sexual maturity; Wikimedia Commons; spiral; Mathematical model of floret arrangement; pattern; seed; sunflower; petal; flower; daisy; four-leaf clover; leaf; leaves; plant stem; phyllotaxis; Alan Turing; leopard; spot; American Association for the Advancement of Science; physics; biology; mathematical biologist; D'Arcy Thompson; Alan Newell; University of Arizona; Allen Newell; computer scientist; mechanics of materials; Galileo; organism; square-cube law; Two New Sciences (1638); volume; area; cross-sectional area; gravity; giant; human; elephant; On Growth and Form; Crocodylus porosus (saltwater crocodile); american crocodile (Crocodylus americanus, or Crocodylus acutus; buckling; tissue; stress; free energy; theory; experiment; sample size; University of Manchester; Museum of Science and Industry; Manchester Science Festival; Matt Pennybacker.