| Tikalon Blog is now in archive mode.
An easily printed and saved version of this article, and a link
to a directory of all articles, can be found below: |
|
This article |
| Directory of all articles |
Packing and Filling
May 17, 2012
I wrote about packing in a
previous article (Packing, November 30, 2010). When my
wife and I were first
married, one of the first problems we faced was a packing problem. We needed to combine all our possessions into a single small
apartment. After the
initial condition, the situation was self-regulating, since
students never have much money to buy additional
household items.
Secure transmission of data without the encumbrance of
key transfer is an important part of the
Internet. We wouldn't want our financial information zipping along through multiple
routers unprotected. The packing process was viewed as an early means for
public key encryption of data. The
Merkle–Hellman knapsack cryptosystem is a public key
cipher that's based on the
knapsack problem, the idea of which is the optimal packing of items in a
knapsack (backpack, rucksack).
The knapsack problem a
"one-way" problem; that is, it's easier to take items out of an optimally packed sack than putting them back in. It can be idealized
mathematically as the
subset sum problem of building a
subset whose sum is zero from a
set of
integers. For example,
Set: {-22, -5, -3, -2, 1, 3, 4, 7, 9, 14, 18)
Subset: {-22, -5, -2, 4, 7, 18}
In the end, the system that was actually used was the different one-way problem that it's easier to
multiply large numbers than
factor them. This encryption method is used on the
web browser that you're using to view this article, even if you're using certain versions of the
Lynx web browser.
An optimal packing of
pennies on a
plane occurs when their centers are on an
hexagonal lattice, giving an areal density of (π/2√3) = 0.9069 (see figure). This was proven mathematically by
Carl Friedrich Gauss for such a lattice packing; and
László Fejes Tóth showed that this is the optimal packing, lattice or otherwise.[1]
Lattice packing of pennies in a plane.
These are Wikipedia pennies, the payment I get for writing Wikipedia articles.
(Based on a Wikimedia Commons image))
The idea of arranging
circles so that they have a maximum
areal density can be extended to filling
geometrical figures; and there's a similar problem of filling geometrical figures with overlapping circles of selected diameters to fill as much of the area as possible (see figure). This filling problem is discussed in a recent paper in
Physical Review Letters by an interdisciplinary team of scientists from the
University of Michigan and the
University of Connecticut.[2-5]
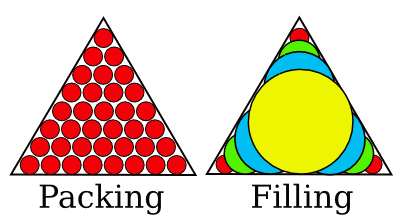
(Illustration by author, rendered with Inkscape)
Filling is an intermediate problem between packing and covering. Covering is the problem of completely covering the surface area of an object with
appliqués of a given shape and size. Filling differs from the covering problem, since the applied shapes can't extend over the shape's
perimeter.[5] An example of the filling problem was given in a
synopsis of this paper on the
American Physical Society web site.
"Imagine you have a square window and you want to block out as much light as possible by taping some opaque circular tiles to the glass. You can use a mixture of tiles with any radius, and they can overlap with each other, but you only have money to buy five."[4]
More technically, filling can be describes as the way you can place N overlapping circles of any size within a bounded area to best fill its area.
In looking at the filling example of the
triangle in the figure, above, you get the idea that there are special lines on which such circles should be placed. These are called the medial lines.
Sharon Glotzer, an author of the study, describes the medial line as the "backbone" of the
polygon. Said Glotzer, "Every shape you want to fill has a backbone that goes through the center of the shape, like a
spine."[5] An example of the medial lines for a
concave polygon and its filling by twenty-one discs are shown in the following figure.
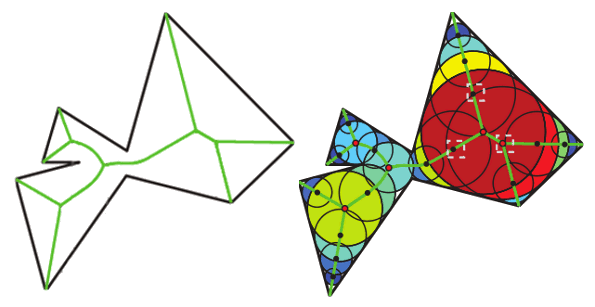
Fig. 2 of reference 3, modified, showing the medial lines for a concave polygon and an optimal filling with twenty-one discs. (Via arXiv Preprint Server).[3)]
It's always nice when research provides a tangible benefit. There are quite a few applications for an effective filling algorithm. The equipment used for
radiation treatment of
tumors allows control of the
beam diameter, so this may be a method for effective treatment with the lowest number of beam shots.[2-3]
It would also allow optimal mapping of
cell telephone towers for best coverage, and programming of
ion beams for the best definition of a shape in
ion-milling or
ion-deposition.[2-3] The research team is polishing an
algorithm that will take as an input a desired shape and the number of discs, and it will output the best disc pattern.[5]
References:
- Weisstein, Eric W. "Circle Packing." From MathWorld--A Wolfram Web Resource.
- Carolyn L. Phillips, Joshua A. Anderson, Greg Huber and Sharon C. Glotzer, "Optimal Filling of Shapes," Physical Review Letters, vol. 108, no. 19 (May 11, 2012), Document No. 198304, 5 pp..
- Carolyn L. Phillips, Joshua A. Anderson, Greg Huber and Sharon C. Glotzer, "Optimal Filling of Shapes," arXiv Preprint Server, February 11, 2012.
- Jessica Thomas, "Thinking Inside the Box," Synopsis of Ref. 2, American Physical Society.
- Katherine McAlpin, "New twist on ancient math problem could improve medicine, microelectronics," University of Michigan Press Release, May 10, 2012.
Permanent Link to this article
Linked Keywords: Wife; marriage; married; apartment; initial value problem; initial condition; student; household; secure transmission; key; cryptography; Internet; router; public key encryption; Merkle–Hellman knapsack cryptosystem; cipher; knapsack problem; knapsack; "one-way" problem; mathematics; subset sum problem; subset; set; integer; multiplication; factor; web browser; Lynx; penny; plane; hexagonal lattice; Carl Friedrich Gauss; Fejes Tóth; Wikimedia Commons; circle; areal density; geometry; geometrical; Physical Review Letters; University of Michigan; University of Connecticut; Inkscape; appliqué; perimeter; synopsis; American Physical Society; triangle; Sharon Glotzer; polygon; spine; concave polygon; arXiv Preprint Server; radiation therapy; radiation treatment; tumor; beam diameter; cell telephone tower; ion beam; ion-milling; ion-deposition; algorithm.