Spaghetti in Physics and Math
January 7, 2011
A traditional
Italian Christmas Eve dinner is a
seafood spectacular. In my own house, we have
shrimp cocktail, followed by
spaghetti with
red clam sauce. Of course, in a
scientist's home, spaghetti is not just a food. It's an object for study. In this article, I present one
physical phenomenon related to the breaking of dry spaghetti; one
mathematics problem that is often posed as a spaghetti problem, although the spaghetti is optional; and one unusual
sorting method that uses spaghetti. Spaghetti - It's not just for dinner anymore!
Spaghetti is a model material for
fracture studies. It's long, it has a uniform cross-section, and it's
brittle. It's not surprising that when you bend a strand of spaghetti beyond a critical
bend radius, it breaks. The surprising thing, however, is that it doesn't break into two pieces, but three; and sometimes more.
Physics Nobelist,
Richard Feynman, noticed this effect. He devoted several hours to some simple
experiments, he generated a few off-the-cuff theories, but he didn't hit on the correct explanation.[1-2] His naked eye observations didn't discover the extremely subtle cause. The key, of course, is the critical bend radius. The first fracture, into two pieces, is easily seen as a consequence of the bend radius having been exceeded. The subsequent breaks are also a consequence of excessive bending, since the initial breakage sends a
flexural wave down the broken pieces.[3-4] High speed photography revealed this cause. It all goes to prove that
theory is fueled by experiment as much as the converse.
Yogi Berra is supposed to
have said,
"In theory there is no difference between theory and practice. In practice there is,"
although the quotation has been attributed also to
Albert Einstein. Solving this spaghetti problem didn't quite command a
Nobel Prize, since there was considerable
prior art, but it did win a 2006
Ig Nobel Award.[5]
The second spaghetti problem is actually a problem in
geometry most easily explicated by spaghetti. It has a long history, since it's been traced back at least to 1854.[6-7] The problem is simply stated:[7]
A spaghetti stick, dropped on the floor, breaks at random into three pieces. What is the probability that the three parts obtained are the sides of a triangle?
The key to the problem is the so-called
triangle inequality, which states that the sum of the lengths of any two sides of a triangle must always exceed the length of the third side. A moment's reflection will reveal that this must be true to build any sort of triangle if you envision the third side to be the base. Ref. 7 gives an
analytical solution. As usual, my programming skill exceeds my mathematical skill, so I did a
Monte Carlo calculation, the source code of which can be found
here. The figure shows a
histogram of successful triangle builds for 10,000 trials of 10,000 broken spaghetti sticks. It's not surprising that the analytical calculation in Ref. 7 gives a 25% probability.
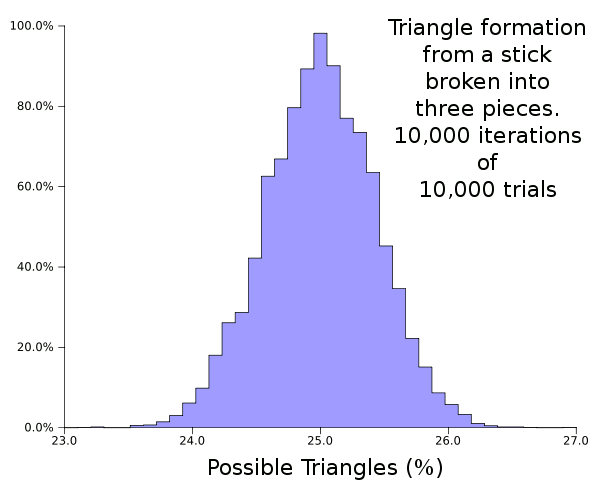
Histogram of 10,000 iterations of 10,000 trials for success in building a triangle from a stick broken into three pieces.
Our last spaghetti-inspired piece of technology is the
spaghetti sort, an
analog sorting technique invented by
Alexander Dewdney, who succeeded
Martin Gardner and
Douglas Hofstadter in writing the recreational mathematics column in
Scientific American magazine. Note that I wrote analog sort. This is not a
computer sort. It's harder to implement (at least with spaghetti), but it runs in
O(N), which is faster than the digital
O(Nlog N). The spaghetti sort is done as follows when you're sorting
real numbers:
1. Scaling so that a full length of spaghetti represents the highest number MAX, prepare a length of spaghetti (n/MAX) for each number n to be sorted. This is done by breaking the spaghetti strand at the proper length and discarding the unneeded piece.
2. Take all the spaghetti strands loosely in your fist and bring them perpendicularly into contact with a tabletop.
3. Pick the longest strand from the stack, note its value, then the next longest, etc.
4. When the strands have all been removed, the sort is done.
Dewdney presented this as an example of how
quantum computing might be able to speed some computations.[8]
References:
- Feynman's Interest in Spaghetti
- RWD Nickalls, "The Dynamics Of Linear Spaghetti Structures," June 14, 2006 (PDF File)
- Basile Audoly and Sébastien Neukirch, "Fragmentation of Rods by Cascading Cracks: Why Spaghetti Does Not Break in Half," Phys. Rev. Lett., vol. 95, no. 9 (25 August 25, 2005), Document 95.095505 (4 pages).
- Josh Gladden, Nestor Handzy, Andrew Belmonte and Emmanuel Villermaux, "Dynamic Buckling and Breaking of Thin Rods."
- James Riordon, "Physical Review Letter on Breaking Spaghetti Leads to 2006 Ig Nobel Award," American Physical Society Press Release, October 6, 2006.
- G.S. Goodman, "The problem of the broken stick reconsidered," Math. Intelligencer, vol. 30, no. 3 (2008), pp. 43-49.
- Eugen J. Ionascu and Gabriel Prajitura, "Things to do with a broken stick," arXiv Preprint (September 5, 2010).
- A.K. Dewdney, "On the spaghetti computer and other analog gadgets for problem solving", Scientific American, vol. 250, no. 6 (June, 1984). pp. 19-26.
Permanent Link to this article
Linked Keywords: Italian cuisine; Christmas Eve; seafood; shrimp; spaghetti; tomato sauce; clam; scientist; physics; mathematics; sorting algorithm; fracture; brittle; bend radius; Physics Nobelist; Richard Feynman; experiment; flexural modulus; wave; theory; Yogi Berra; Albert Einstein; Nobel Prize; Euler-Bernoulli beam equation; Ig Nobel Award; geometry; probability theory; triangle; triangle inequality; analytical solution; Monte Carlo calculation; histogram; spaghetti sort; analog; Alexander Dewdney; Martin Gardner; Douglas Hofstadter; Scientific American magazine; computer; Big O notation; O(N); O(Nlog N); real numbers; quantum computing.