Partitioning
February 21, 2011
When I was a
schoolboy, one way that teachers would keep students busy when they needed a break was to write a long word or a phrase on the
blackboard and have the class try to make as many words as possible from the available letters.[1] There's an
inverse problem in
mathematics that considers how many different ways you can create a
natural number by summing other natural numbers. This process, called
partitioning, generates quite a few more pages of numbers than
factoring, which is the process of finding what
prime numbers multiply together to give you your
composite number.
For example, the number six is the product of two prime numbers, 2 and 3, multiplied together; that is, 2 x 3 = 6. The number of ways you can build six by adding natural numbers takes quite a bit more page space:
6 = 6
6 = 5 + 1
6 = 4 + 2
6 = 4 + 1 + 1
6 = 3 + 3
6 = 3 + 2 + 1
6 = 3 + 1 + 1 + 1
6 = 2 + 2 + 2
6 = 2 + 2 + 1 + 1
6 = 2 + 1 + 1 + 1 + 1
6 = 1 + 1 + 1 + 1 + 1 + 1
So, there are eleven ways to sum natural numbers to get six. The number of ways to generate the natural numbers this way, starting with zero, is called the partition function and is symbolized as p(n), where n is the natural number. The partition function is the integer sequence, 1, 1, 2, 3, 5, 7, 11, 15, 22, 30, 42, 56, 77, 101, 135, 176, 231, 297, 385, 490, 627, 792, 1002, etc.. This is sequence
A000041 of the
The On-Line Encyclopedia of Integer Sequences, and its low accession number underscores its fundamental nature. The graph below shows how the number of partitions grows as the natural numbers become larger. The partition of 1000 is given as
p(1000) = 24,061,467,864,032,622,473,692,149,727,991,
or about 2.4 x 10
31.
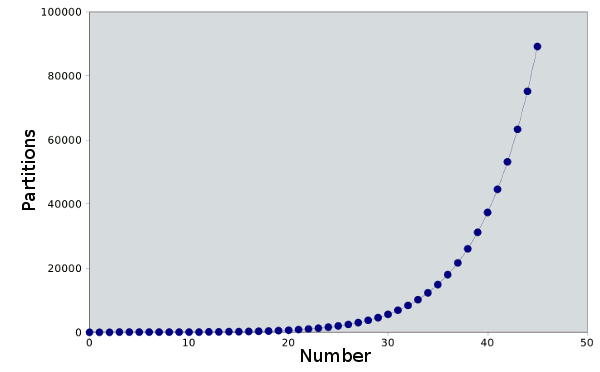
Partitions for the natural numbers up to 45. Not exactly an exponential, but quite close for large n. Rendered via Gnumeric with data from my C program.
Until recently, there was no
function available for calculating values of p(n). Not surprisingly,
Leonhard Euler attempted a formula, and he was successful in finding a
recursion relation instead. The recursion relation gives accurate values, but it's too complicated for use on very large numbers. I've translated into C a published Basic program[2] that uses Euler's method to calculate the number of partitions for natural numbers up to 121, the limit of a long integer in C. You can view the source code
here.
In 1918, the famous number theorists,
G. H. Hardy and
Srinivasa Ramanujan, showed that the partition function was quite closely approximated by an
exponential. At the time, Ramanujan, who had a head for numbers, to say the least, noticed patterns in the partition number sequence involving the
prime numbers 5, 7 and 11. These are known as
Ramanujan's congruences.
Robert Kanigel, a professor of science writing at
MIT, has written a biography of Ramanujan, readable by non-mathematicians, that sits on my bookshelf.[3]
Hans Rademacher found an exact formula for p(n) in 1937; but it was still complicated; and, as they say, it lacked
elegance, since it used a construct called a modified
Bessel function of the first kind. Finally, it was announced at the end of January that
Ken Ono, in collaboration with many other mathematicians, had discovered a finite formula determining the value of p(n) for positive n.[4-8] Ono is a chaired professor at the
University of Wisconsin-Madison and at
Emory University, and the partition team included Jan Bruinier (
Technical University of Darmstadt, Germany), Amanda Folsom (
Yale) and Zach Kent (Emory).[4]
This partition formula had a strange genesis in
Fry's Electronics, a
US West Coast electronics retailer that helped to fuel the later
silicon valley hacker culture responsible for many of our computer gizmos.
John Fry, the company
CEO, founded and funded the
American Institute of Mathematics (
Palo Alto, California) in 1994. The American Institute of Mathematics became a
National Science Foundation mathematical institute, one of seven, in 2002. The Institute encourages collaboration on major mathematics problems by hosting workshops on current topics, and that's how the partitioning team was started.[4]
I've written often how many discoveries have happened by accident, or by a flash of insight. A flash of insight is what led to the partition formula. As recounted in an Emory University press release, Ken Ono and Zach Kent were hiking in northern
Georgia, about an hour and a half drive northeast of Emory. They started to imagine what it would be like to hike through partition numbers and realized that partition numbers had a
fractal nature; that is, they had an infinitely-repeating structure.[4]. This
self-similarity of fractals, as applied to partitioning, removed the problems with Rademacher's approach of nearly a hundred years ago.
The insight also confirmed Ramanujan's idea of congruences. Says Ono, "The sequences are all eventually periodic, and they repeat themselves over and over at precise intervals."[4] Another mathematician,
Frank Calegari of
Northwestern University, has developed a shorter proof.[7]
References:
- Despite persistent rumors, I'm not as old as to have been a classmate of Irving Langmuir. A more challenging word game is Euler's Day Off, for which the goal is placement of twenty-five random letters in a five-by-five grid to yield as many vertical and horizontal words as possible. Only words with three or more letters count, and the game is scored by assigning one point for each word letter.
- Abdulkadir Hassen and Thomas J. Osler, "Playing With Partitions On The Computer."
- Robert Kanigel, "The Man Who Knew Infinity: A Life of the Genius Ramanujan," (Washington Square Press, New York), 1991, 464 pages (Paperback via Amazon).
- Carol Clark, "New theories reveal the nature of numbers," Emory University Press Release, January 20, 2011 .
- Jan Hendrik Bruinier And Ken Ono, "An Algebraic Formula For The Partition Function," AIM Web Site.
- Amanda Folsom, Zachary A. Kent and Ken Ono, "l-Adic Properties Of The Partition Function," AIM Web Site.
- Frank Calegari, "A Remark On A Theorem Of Folsom, Kent, And Ono," Northeastern University.
- American Institute of Mathematics, What is the partition function?
Permanent Link to this article
Linked Keywords: Schoolboy; blackboard; inverse problem; mathematics; natural number; partitioning; factoring; prime numbers; composite number; Integer Sequence A000041; The On-Line Encyclopedia of Integer Sequences; Gnumeric; function; Leonhard Euler; recursion relation; G. H. Hardy; Srinivasa Ramanujan; exponential; prime number; Ramanujan's congruences; Robert Kanigel; Massachusetts Institute of Technology; MIT; Hans Rademacher; elegance; Bessel function; Ken Ono; University of Wisconsin-Madison; Emory University; Technical University of Darmstadt, Germany; Yale; Fry's Electronics; US West Coast; silicon valley; hacker culture; John Fry; CEO; American Institute of Mathematics; Palo Alto, California; National Science Foundation; Georgia; fractal; self-similarity; Frank Calegari; Northwestern University; Irving Langmuir; Euler's Day Off.