| Tikalon Blog is now in archive mode.
An easily printed and saved version of this article, and a link
to a directory of all articles, can be found below: |
|
This article |
| Directory of all articles |
Slimy Computation
September 15, 2011
Science was not always a noble profession. The early practice of
chemistry, as
alchemy, was not well regarded, since it was a refuge for
charlatans promising to change
lead to
gold or offering to cure incurable illnesses. There have been some isolated transgressions in today's science, such as falsification of data,
plagiarism, and
Ph.D.s selling items of dubious benefit on
cable television, but our profession is generally clean. Perhaps I should include the occasional stretching of the truth on presentations to corporate management and funding agencies.
The adjective, "slimy," is not typically applied to science, except for the areas of
biology that actually involve actual
slime. The adjective, "slimy," is usually reserved for description of certain sectors of the
financial industry. We certainly don't expect to hear about anything slimy in
computer science. That's why a series of papers by
Andrew Adamatzky, a professor of computer science at the
University of the West of England (Bristol, UK), is so interesting. These papers describe computations by
slime mould.[1-3]
First, a comment on
nomenclature. I was taught to spell mould as "mould." This makes a lot of sense, since it eliminates the confusion between the type of
mold used to make shapes. Unfortunately, the shaping mold is sometimes spelled as mould, too. Apparently the British
prefer words like colour and flavour, while Americans prefer their u-barren alternates. My weekly reading of
Nature has likely reinforced my mouldy habits.
Adamatzky describes himself as a "Professor in Unconventional Computing in the Department of Computer Science, ranger of the Unconventional Computing Centre, and a member of Bristol Robotics Lab." He's the
Editor in Chief of the
International Journal of Unconventional Computing and the
Journal of Cellular Automata, and the author of
numerous books and
journal articles.
Using slime mould to solve problems is an example of
metaheuristic problem solving using the slime mould itself as the computer.
Ant Colony Optimization (ACO) is a related approach that takes its inspiration from the way that ants find a direct pathway from food to their colony. This same strategy is useful for things such as routing messages in a
network, the placement of
conductor traces on a
printed circuit board, and solving the
Travelling Salesman Problem.
While searching for food,
ants initially wander aimlessly in a random search. When an ant finds food, it returns to its colony, and during his return he lays down a trail of a
pheromone. Other ants will tend to remain on this pheromone trail, find the food source, and intensify the trail with their own pheromones on their return to the colony.
The pheromone will
evaporate, and, as a result, short paths with the most pheromone are favored. The ants'
algorithm avoids
convergence to a
locally optimal solution, such as going the too long way around a large rock.
The slime mould,
Physarum polycephalum, is a large
cell organism that's visible with the naked eye. The mould exhibits
foraging behavior reminiscent of the ant example, above.[1] When an
oat flake is placed at the center of a
maze as an attractant, an
inoculated mould will grow a pronounced
protoplasmic tube towards the attractant.
This protoplasmic tube is the solution of the maze that's driven by the
gradient of chemical attractants propagating from the target. A video is available at
http://www.youtube.com/user/PhysarumMachines.[4] A similar
experiment reconstructed an approximation of the
Mexican Federal Highway System linking nineteen major cities that were marked by oat flakes. The mould was inoculated at
Mexico City.[5]
Maze-solving with the plasmodium, P. polycephalum. The figures show the maze, and the path of the mould from the point of inoculation to an oat flake placed at the center. A video is available at
http://www.youtube.com/user/PhysarumMachines. (Via arXiv, Ref. 1).
Leaving the slime world and entering the realm of
crystallization that was one of my specialties, Adamatzky has examined the use of crystallization kinetics in computing segmentation.[6] I reviewed Voronoi tessellation in a
previous article (Segmentation, June 28, 2011). The common chemical,
sodium acetate, can solve a planar segmentation problem for points represented by crystal nuclei. As can be seen in the figure, the crystal domains instantiate a
Voronoi tessellation for the crystal nuclei.
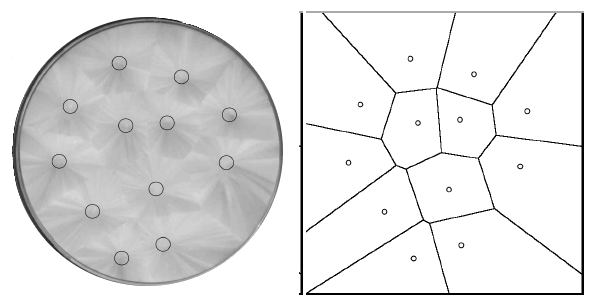
Voronoi tessellation of crystal nucleation points in sodium acetate. (Via arXiv, Ref. 6).
References:
- Andrew Adamatzky, "Slime mould solves maze in one pass ... assisted by gradient of chemo-attractants," arXiv Preprint Server, August 24, 2011.
- Andrew Adamatzky, "Slime mould logical gates: exploring ballistic approach," arXiv Preprint Server, May 13, 2010.
- Andrew Adamatzky, "Slime mould computes planar shapes," arXiv Preprint Server, June 1, 2011.
- Physarum Machines on YouTube.
- Physarum Approximation of Mexican Federal Highways, YouTube Video.
- Andrew Adamatzky, "Hot Ice Computer," arXiv Preprint Server, August 30, 2009.
Permanent Link to this article
Linked Keywords: Science; chemistry; alchemy; charlatan; lead; gold; plagiarism; Doctor of Philosophy; Ph.D.; cable television; biology; slime; financial industry; computer science; Andrew Adamatzky; University of the West of England (Bristol, UK); slime mould; nomenclature; mold; Nature; Editor in Chief; International Journal of Unconventional Computing; Journal of Cellular Automata; metaheuristic; Ant Colony Optimization (ACO); computer network; electrical conductor; printed circuit board; Travelling Salesman Problem; ant; pheromone; evaporation; algorithm; convergence; locally optimal solution; Physarum polycephalum; cell; organism; foraging behavior; oat; maze; inoculation; protoplasmic; gradient; experiment; Mexican Federal Highway System; Mexico City; crystallization; sodium acetate; Voronoi tessellation.