Marriage Problems in Math
March 4, 2011
There's a cute
teen/
tween television series on
Nickelodeon called
iCarly. Surprisingly, no
vampires are involved. I mentioned iCarly in a
previous article about
base-11 numbers (The Number Dirf, November 23, 2010). In one episode of the show, "iDream of Dance,"[1] the three tween protagonists announced a video contest on their web site and got a huge response. As a result, they needed to screen three thousand video clips, a task they decided to do as six nights of five hundred videos a night. A little mathematical magic, as I'll reveal below, shows that they might have reduced their workload by a significant percentage.
There are at least two math problems known as "marriage" problems. One is called the "
stable marriage problem," which I'll review later. The other is simply "
the marriage problem," although it's known by other names, such as the "fussy suitor problem" and the "secretary problem." The problem is an
optimal stopping problem, sort of like a law of
diminishing returns when selecting from a group. The goal is a process that will likely result in your choosing the best candidate without interviewing everyone. The problem is simply stated.[2]
• There is a single position to fill. You're looking for either a secretary to hire, or a wife.
• There's a known number of applicants for the position.
• It's possible to rank the applicants from best to worst, with no ties.
• You interview the applicants sequentially in a random order.
• After each interview, you can accept or reject the candidate.
• Your decision can be based only on the relative ranks of the applicants that you've interviewed to that point.
• When you reject an applicant, that applicant can't be recalled.
• When you accept an applicant, the remaining interviews are canceled.
• You want to select the best applicant.
The solution to this problem is often called the 37% rule because the optimum
strategy is to decide that you have enough information to make a wise choice after interviewing
1/e people, where
e is
the base of natural logarithms. Since
e = 2.71828..., then
1/e is 0.367879..., and we get about 37%. If we interview 37% of the candidates, and then choose the next candidate better than any one of these, we have a good chance of having made the best choice. Even if we somehow don't get the very best, we're not that far wrong. One caveat, however, is that we're sometimes forced to choose the last person on the interview list, no matter what her qualifications.
It's very easy to write a program to analyze this problem, so I did. You can view the C source code,
here.
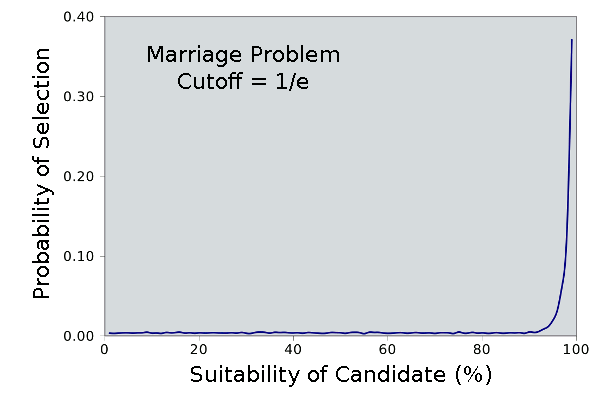
The probability of selection as a function of candidate suitability for the marriage problem using the 1/e cutoff rule. Graphics via Gnumeric.
So, how good is our choice when we decide to use the
1/e rule? The graph above, which uses data from my analysis program, tells the story. The program did ten thousand trials of interviews of a hundred candidates for various cutoffs, including
1/e. If we use the
1/e cutoff, then we're about 37% likely to find the best candidate. Even if we don't find the very best, our odds of finding a very good candidate are quite high, as the following table shows. There's about a 63% chance that you'll get someone in the top 5%.
| Rank | Likelihood (%) |
| 1 | 37.10 |
| 2 | 13.63 |
| 4 | 6.46 |
| 4 | 3.38 |
| 5 | 1.96 |
| 6 | 1.17 |
| 7 | 0.85 |
| 8 | 0.55 |
| 9 | 0.43 |
We can even be a little lazy about our cutoff, as the figure below shows. There's a broad band about the 37%,
1/e rule, for which the probability of selecting the best candidate stays about the same.
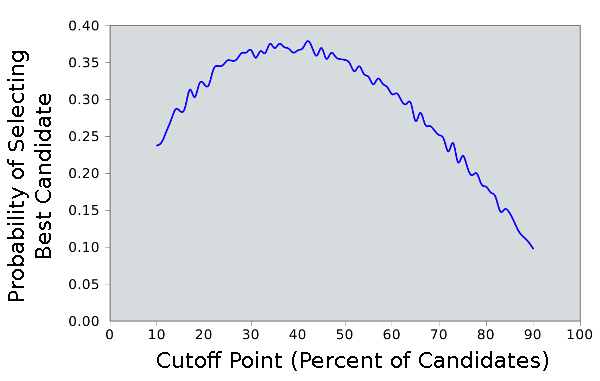
The probability of selecting the best candidate as a function of cutoff for the marriage problem. There a wide range around the 1/e cutoff where the probability is essentially the same. Graphics via Gnumeric.
The other mathematical marriage problem is the
stable marriage problem. This problem is more complicated than the marriage problem analyzed above. Essentially, you have a group of men and a group of women of equal number, and the individuals of each group rank the suitability of all individuals of the other group (Sorry, no "
civil unions" are considered here). The
optimization problem in this case is to match men and women such that there's no man and woman who would rather have each other than their current partner. It might be worthwhile to reread that last sentence. It doesn't mean that every man gets the woman of his dreams, and vice-versa. It just means that any lusting is
unrequited.
It's been proven that such a matching is always possible, and there's a simple
algorithm to do the matching. I didn't write a C implementation; but, as the textbook authors say, "The exercise is left to the reader." It's not surprising that there's a related problem, the "
stable roommates problem," that's more useful. In this case, all participants are in the same pool. Unfortunately, the stable roommates problem may not always have a solution, so it's probably still better to marry than to just live together.
References:
- iCarly Television Series, Season 1, Show 3, "iDream of Dance," Adam Weissman, Director, Dan Schneider, Writer, September 16, 2007.
- Tom Ferguson, "Who Solved the Secretary Problem?" Statistical Science, vol. 4, no. 3, pp. 282-296.
Permanent Link to this article
Linked Keywords: Teen; tween; Nickelodeon; iCarly; vampires; dirf; base-11 numbers; stable marriage problem; the marriage problem; optimal stopping problem; diminishing returns; strategy; the base of natural logarithms; Gnumeric; stable marriage problem; civil union; optimization; unrequited love; algorithm; stable roommates problem; iDream of Dance.