| Tikalon Blog is now in archive mode.
An easily printed and saved version of this article, and a link
to a directory of all articles, can be found below: |
|
This article |
| Directory of all articles |
Crumpled Paper
October 25, 2011
As I wrote in a
previous article (Paper Chase, September 7, 2010), there's a lot of
physics in a sheet of
paper. Starting a little more than a decade ago,
physicists began investigating a commonplace process, crumpling of sheets of paper and other materials, and they found some universal laws.
In the mid-1990s, physicists at the
The University of Chicago crumpled
Mylar sheets and recorded the emitted sound. The sound appeared as discrete clicks with
amplitudes that ranged over six
orders of magnitude.[1-2] These amplitudes are related to the
deformation energy, and the energy was found to be distributed according to a
power law distribution,
P(E) ∼ e-α
where
P(E) is the
probability of a click having energy
E, and
α is about one. The power law didn't change when the sheet material or size of the sheet was changed, so it's a universal law.[2]
Possibly an image of one of my first manuscipts, after review by the journal editor.
We still wrote things on paper in those days.
(Via Wikimedia Commons))
Other researchers have found a power law relationship between the height of a crumpled ball and the
weight of a
compressing mass; between the number of crumple creases and the
radius of the ball; between the mean length of a crease and the ball radius; and between the mean length of a crease and the number of creases.[1,3]
Crumpled balls of paper are
mechanically stiff, and it takes quite a bit of
force to crumple them further. This is remarkable, since a typical crumpled ball of paper is 75% air.[1]
Of course, physicists are not just satisfied with making observations such as these. They're always looking for
principal causes, so they probe more deeply into the structure of the system. A first attempt at this was done in 2009 by Chinese physicists, Yen-Chih Lin, Ji-Ming Sun, H. W. Yang, Yeukuang Hwu, C. L. Wang and Tzay-Ming Hong, who used
X-ray tomography on crumpled
aluminum foil balls to reveal their internal structure.[4-5]
In all cases, the foil was 16
μm thick, and the balls of final radius 1.5
mm were crumpled from circular radius sheets ranging from 3-10 mm. Using a 10
keV X-ray beam, they were able to form (1200 x 1200 x 1200)
pixel data matrices with 3 μm resolution. They found that the internal
geometric fractal dimension increases with compression, and the mass distribution changes from
inhomogeneous to uniform.[4-5]
At low
volume fraction, the mass distribution is inhomogeneous with a fractal dimension somewhat larger than two. As the crumpled balls are compressed further, the mass distribution becomes homogeneous as the fractal dimension increases to about 2.8. The theory behind this behavior is that compression diminishes free spaces to add newly crumpled layers, so the existing layers have nothing else to do but
buckle. Compressed balls at this point mechanically resemble packed
granular materials, which have a
porous structure that is homogeneous in mass distribution.[4-5]
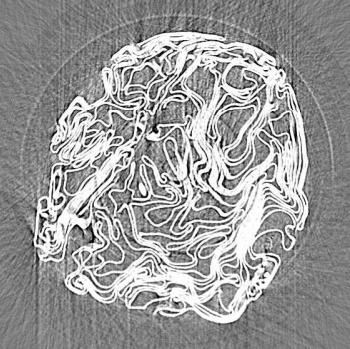
X-ray tomograph section of a compressed aluminum foil ball.
This image was constructed from a thousand projections for a ball for which the radius was compressed by a factor of six.
(Fig. 1 of Ref. 5, via arXiv))
Just recently,
Anne Cambou, a graduate student at the
Department of Physics,
University of Massachusetts (Amherst, MA), and Professor
Narayanan Menon decided to go a step further with such spatial analysis by examining the three-dimensional structure of crumpled sheets, including the distribution of curvature and orientation. They first tried this using
confocal microscopy on thin, crumpled
polymer sheets, but they reverted to X-ray tomography using a machine in the
geology department of
Amherst College.[6]
Cambou and Menon found that the distribution of curvature and local sheet orientation were almost perfectly isotropic and homogeneous. As an example, even the surface of the ball was only slightly more likely to contain sheets oriented parallel to the surface than in other directions. This is a local
nematic ordering. In nematic ordering, the unit shapes of the material run parallel to each other.[7-8]
Cambou and Menon intend to refine their optical technique so that they can do experiments on the
dynamics of crumpling. This is a far more complex task that requires rapid data acquisition, but such interesting results warrant a follow-up. As they remark in their paper in the
Proceedings of the National Academy of Sciences,
"...Crumpling recapitulates other classic nonequilibrium problems such as turbulence, where a system driven by long-wavelength, low-symmetry, forcing shows only rather subtle fingerprints of the forcing mechanism."[7]
References:
- Ivars Peterson, "Deciphering the Wrinkles of Crumpled Sheets," Ivars Peterson's MathTrek (Mathematical Association of America, May 26, 2003).
- Eric M. Kramer and Alexander E. Lobkovsky, "Universal power law in the noise from a crumpled elastic sheet." Phys. Rev. E, vol. 53 (1996), pp. 1465-1469.
- Alexander E. Lobkovsky and T. A. Witten, "Properties of ridges in elastic membranes," Phys. Rev. E, vol. 55 (1997), pp. 1577-1589.
- Yen-Chih Lin, Ji-Ming Sun, H. W. Yang, Yeukuang Hwu, C. L. Wang and Tzay-Ming Hong, "X-ray tomography of a crumpled plastoelastic thin sheet," Phys. Rev. E, vol. 80, no. 6 (December 16, 2009), Document No.066114 (6 pages).
- Yen-Chih Lin, Ji-Ming Sun, H. W. Yang, Yeukuang Hwu, C. L. Wang and Tzay-Ming Hong, "X-ray tomography of a crumpled plastoelastic thin sheet," arXiv Preprint Server, December 18, 2009.
- Johanna L. Miller, "What's inside a crumpled ball?" Physics Today, vol. 64, no. 10 (October, 2011), p.15.
- Anne Dominique Cambou and Narayanan Menon, "Three-dimensional structure of a sheet crumpled into a ball," Proc. Natl. Acad. Sci., vol. 108, no. 36 (September 6, 2011), pp. 14741-14745.
- Supporting Information for Cambou and Menon, Ref. 7.
Permanent Link to this article
Linked Keywords: Physics; paper; physicists; The University of Chicago; Mylar; amplitude; order of magnitude; deformation; energy; power law distribution; probability; Wikimedia Commons; weight; compressing mass; radius; stiffness; mechanically stiff; force; principal cause; X-ray tomography; aluminum foil; μm; mm; electronvolt; keV; X-ray; pixel; matrix; geometric fractal dimension; homogeneity; heterogeneity; inhomogeneous; uniform; volume fraction; buckling; granular material; porous; arXiv; Anne Cambou; Department of Physics; University of Massachusetts (Amherst, MA); Narayanan Menon; confocal microscopy; polymer; geology department; Amherst College; nematic; Proceedings of the National Academy of Sciences.