| Tikalon Blog is now in archive mode.
An easily printed and saved version of this article, and a link
to a directory of all articles, can be found below: |
|
This article |
| Directory of all articles |
The Collatz Conjecture
April 14, 2011
Iteration is a large part of our lives. We seem to do the same things, again and again. Any given day of our week is likely a
carbon copy of that same day the week before. This repetition was much more regular to our
agrarian ancestors; so much so, that they had a different concept of time. The idea of "
deep time" was unknown to them, since they had no conception that the
Earth, which was their
universe, had a beginning and would have an end. Time to them was cyclic. The same things happened over and over, whether by the day or by the season.
One of the most important constructs in
computer programming is the
loop, which uses iteration in a useful fashion. Iteration is built into
mathematics in
series expansions, which have given us very accurate values for the
trigonometric functions, and many digits of
pi. The
Newton–Raphson method, a method for refining calculation of
roots, is another useful iterative technique.
There's a "dark side" of iteration; namely, those iterations that don't converge to a simple result. Iteration is at the heart of the
Mandelbrot set.
John von Neumann proposed the following iteration as a
random number generator.[1]
xn+1 = 4xn(1 - xn)
There's prior art to this in the work of
Gauss, who remarked on the complexity of the iteration,[1]
xn+1 = FractionalPart[1/xn]
A random number generator that was popular in the early computing days of slow clock rates and small memories is an iteration called the
linear congruential generator (LCG),
xn+1 = (axn + b) mod m
Common values for the LCG parameters are m = 2
32, a = 1664525 and b = 1013904223. The sequence is seeded by any x
0 value between 0 and m.
The
logistic map is an iteration that produces a variety of responses dependent on its initial parameter. The equation is
xn+1 = rxn(1 - xn)
The logistic map produces a
chaotic sequence for r values between 3.57 and 3.83.
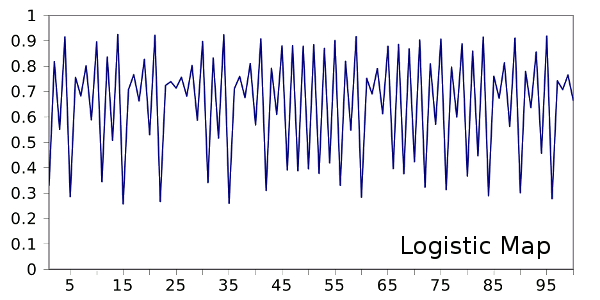
Logistic map for an initial value of 0.33 and r = 3.7. (Plot via Gnumeric)
The
Collatz conjecture is a conjecture involving the progression of values of an iteration. Unlike the iterations above, the Collatz iteration has a
condition statement thrown in. This number sequence is constructed as follows:
1) Start with a natural number, n0
2) If n is even, then ni+1 = ni/2
3) If n is odd, then ni+1 = 3ni + 1
4) Continue at step (2) until n = 1
As you can see, step 2 will always decrease n, and step 3 will always increase n, so you can expect some random up-down action. What you don't expect is that you always terminate in n = 1, no matter the value of n
0. The
conjecture is that this is always the case. The following plot shows the sequence starting at n = 983, as generated by
this program.
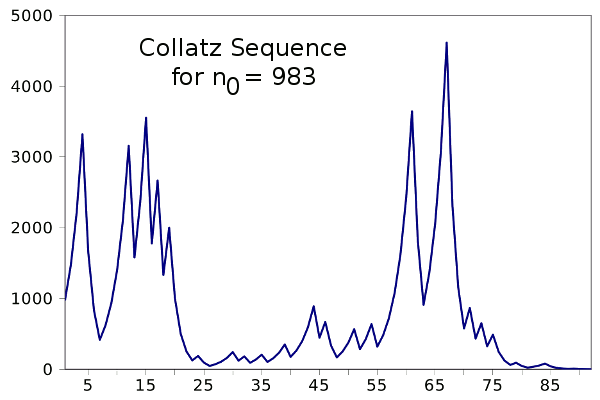
Collatz sequence starting with n = 983. (Plot via Gnumeric)
Lest you think that larger numbers will favor longer sequences, look at the sequences for the numbers 27 and 908:
27 → 41 → 62 → 31 → 47 → 71 → 107 → 161 → 242 → 121 → 182 → 91 → 137 → 206 → 103 → 155 → 233 → 350 → 175 → 263 → 395 → 593 → 890 → 445 → 668 → 334 → 167 → 251 → 377 → 566 → 283 → 425 → 638 → 319 → 479 → 719 → 1079 → 1619 → 2429 → 3644 → 1822 → 911 → 1367 → 2051 → 3077 → 4616 → 2308 → 1154 → 577 → 866 → 433 → 650 → 325 → 488 → 244 → 122 → 61 → 92 → 46 → 23 → 35 → 53 → 80 → 40 → 20 → 10 → 5 → 8 → 4 → 2 → 1
908 → 454 → 227 → 341 → 512 → 256 → 128 → 64 → 32 → 16 → 8 → 4 → 2 → 1
All this adds to the mystery of this sequence.
This interesting recursion was discovered in 1932 by
Lothar Collatz, who was at the time a twenty year old mathematics student. As discussed in an entertaining book of number anecdotes by George Szipiro,[2] the Collatz conjecture has had many names over the years before reverting to that of its discoverer. It was popularized in the US by
Stanislaw Ulam, who introduced it to the extremely talented corp of people who worked with him on the
Manhattan Project.
For a time after that it was known as Ulam's problem. Then it became known as the
Hailstone sequence because of the similarity of the up-down motion of its numbers to the process of hailstone formation. It was also known as the
Kakutani problem, after another mathematician who worked on the conjecture. We shouldn't be too surprised at this, since it happened in the days before
computer-assisted search.
References:
- Stephen Wolfram, "A New Kind of Science," Wolfram Media, May 14, 2002, page 918.
- George G. Szipiro, "The Secret Life of Numbers," Joseph Henry Press (Washington, D.C., 2006), Chapter 6 ("A Puzzle by Any Other Name"). pp. 20-23 (Via Amazon).
Permanent Link to this article
Linked Keywords: Iteration; carbon copy; agrarian ancestors; deep time; Earth; universe; computer programming; loop; mathematics; series expansion; trigonometric functions; pi; Newton–Raphson method; nth root; Mandelbrot set; John von Neumann; random number generator; Carl Friedrich Gauss; linear congruential generator; logistic map; chaotic sequence; Gnumeric; Collatz conjecture; condition statement; conjecture; Lothar Collatz; Stanislaw Ulam; Manhattan Project; hailstone; Shizuo Kakutani; web search engine; computer-assisted search; Stephen Wolfram; A New Kind of Science; George G. Szipiro; The Secret Life of Numbers.