Hyper-Spinning Regulus
May 4, 2011
It's no surprise to anyone with a mechanical sensibility that a spinning orb of
elastic matter will bulge at its
equator. This is true even when the material is not that elastic, like the rocks that comprise the
Earth's crust, so the Earth has a
bulge at its equator. The Earth differs somewhat from a
sphere; it's an
oblate spheroid with a 42.72
km (26.5
mile) bulge at the equator. The
oblateness of the Earth is given as
Oblateness = (a - b)/a = 0.335%
where a is the distance from the equatorial surface to the Earth's center, and b is the distance from the Earth's
pole to its center.
The
gas giant,
Saturn, has an oblateness of 9.8%. The
Sun's oblateness is only 9 x 10
-6, or 0.0009%, which is a consequence of the large
gravitational force holding it together, and its slow equatorial
rotation rate of 25 days. Contrast this with the
star,
Regulus, which has an estimated rotation rate of about sixteen hours, and an oblateness of about 26%.[1]
Regulus is known also as α Leonis. It's the brightest star in the
constellation Leo, as its "alpha" designation indicates. It's also the twenty-second brightest star (
magnitude 1.35) in Earth's sky. When you consider all the stars visible with the naked eye, twenty-second place is quite a high rank. Regulus is about 77.5
light years from Earth.
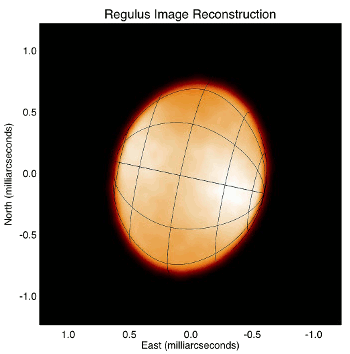
An image of the star Regulus showing its equatorial bulge.
(Image by Xiao Che, University of Michigan)
To say that Regulus is rapidly-spinning is an understatement. Whereas the Sun's equatorial speed is about 4,500 miles per hour, the equator of Regulus, which has a five-fold larger radius than the Sun and a much faster rotation rate, is 700,000 miles per hour. This has more of an impact if we rephrase this number as
nearly a million miles per hour. Seven hundred thousands miles per hour means a
trip from Earth to the
Moon in just twenty minutes. Calculations show that Regulus would fly apart if its rotation rate were just 16% faster.
Rapid spinning has a big effect on
stellar hydrodynamics. The poles of Regulus have a larger surface gravity, and they are hotter and brighter than the equator. The magnitude of this so-called "
gravity darkening" of the equator is usually estimated by the
von Zeipel Theorem,
T ∼ g1/4
in which the
temperature T is proportional to the quarter-power of the local gravity
g. The power is only 0.25 if the local
energy transfer is purely
radiative. It's reduced when
convection is present.[2]
Recently, some
astronomers from the
University of Michigan have used
interferometry to do precise temperature measurements of Regulus.[3-4] A star's temperature is an important predictor of its
age. They combined the
infrared light of four
telescopes at the
CHARA array of
Georgia State University to give a huge effective
aperture instrument they could use to examine particular regions of the star.
They found that the temperature difference between equator and poles is considerably less than the von Zeipel Theorem prediction, and it's more consistent with an exponent of 0.19. This may seem like a small difference, but the effect is amplified in Regulus by the very large difference in effective gravity between the equator and poles. The difference between the von Zeipel prediction and observation is about 2750°C.[4]
The
asteroid 163 Erigone is expected to pass between Regulus and the Earth on March 20, 2014, a so-called
occultation. Occultations were previously the only way to study the fine structure of the asteroids. Now we have
spacecraft. One interesting thing about this occultation is that its path is predicted to pass over my house. The occultation path was calculated by Aldo Vitagliano,[5] and his prediction appears in the figure.
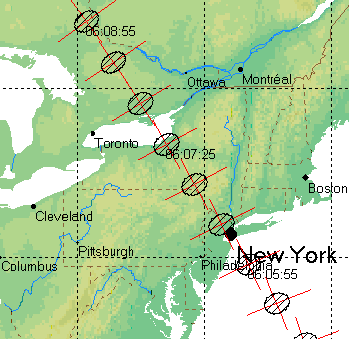
Predicted occultation path of Regulus by asteroid 163 Erigone on March 20, 2014.
(Image by Aldo Vitagliano, Ref. 5, Modified.)
![]()
References:
- Lorenzo Iorio, "The impact of the oblateness of Regulus on the motion of its companion," arXiv Preprint Server, August 20, 2008.
- H. Rovithis-Livaniou, "The Gravity Darkening Effect: From Von Zeipel Up To Date," Bulgarian Academy of Sciences, Space and Solar-Terrestrial Research Institute Web Site, (No Date).
- Nicole Casal Moore and Jim Erickson, "Zoom-up star photos poke holes in century-old astronomical theory," University of Michigan Press Release, April 18, 2011.
- X. Che, J. D. Monnier, M. Zhao, E. Pedretti, N. Thureau, A. Mérand, T. ten Brummelaar, H. McAlister, S. T. Ridgway, N. Turner, J. Sturmann and L. Sturmann, "Colder And Hotter: Interferometric Imaging Of β Cassiopeiae And α Leonis," The Astrophysical Journal, vol. 732, no. 2 (May 10, 2011), p. 68.
- Aldo Vitagliano, The SOLEX page. Full Occultation chart appears here.
Permanent Link to this article
Linked Keywords: Elasticity; elastic; equator; Earth; crust; equatorial bulge; sphere; oblate spheroid; kilometer; km; mile; flattening; oblateness; geographical pole; gas giant; Saturn; Sun; gravitation; gravitational force; rotation period; rotation rate; star; Regulus; constellation Leo; apparent magnitude; light year; Xiao Che; Orbit of the Moon; Moon; stellar structure; stellar hydrodynamics; gravity darkening; von Zeipel Theorem; temperature; energy; radiative cooling; convection; astronomer; University of Michigan; interferometry; Hertzsprung-Russell diagram; infrared light; telescope; CHARA array; Georgia State University; aperture; asteroid; 163 Erigone; occultation; spacecraft; Aldo Vitagliano.