| Tikalon Blog is now in archive mode.
An easily printed and saved version of this article, and a link
to a directory of all articles, can be found below: |
|
This article |
| Directory of all articles |
Maxwell, Boltzmann and Brown
September 14, 2011
In the early days of
physics, many things needed to be taken on faith (i.e., belief in
theory), since direct
experimental observations of the principal mechanisms were not possible. One case in point is the
Maxwell-Boltzmann distribution of
molecular velocities in a
gas that describes the mean
pressure. It isn't possible to observe the actual molecules and verify the distribution, but everything seems to work, so we push the verification into the future.
The future in that case was more than one hundred years distant, when in 2010,
physicists from the
Center for Nonlinear Dynamics and Department of Physics, the
University of Texas at Austin (Austin, Texas), did an indirect, but satisfying, measurement that used
Brownian motion.[1-2] Brownian motion is the
random motion of particles in
fluids that's presumably caused by their being impacted by the molecules of the fluid.
Brownian motion was first observed in 1827 by the
botanist,
Robert Brown, who was doing
microscopic studies of
pollen grains. Pollen contains extremely small, subsidiary particles, the
amyloplasts and
spherosomes, that Brown saw to be in a continual jittery motion.
Good
scientist that he was, he repeated his observation with
inorganic particles to rule-out any
life-related principle, but he could not suggest an explanation. Brownian motion is still an active research study after all these years. The
arXiv preprint server had 194 articles with "Brownian" in their title posted in 2010.
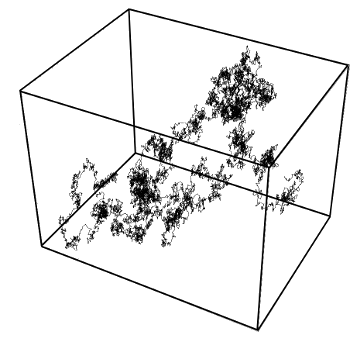
Brownian motion in three dimensions.
This simulation was done using the Wiener process, named for Norbert Wiener.
(Image by T.J. Sullivan, via Wikimedia Commons))
The Texas team analyzed the Brownian motion of
micrometer-sized silica glass beads in
air, held in place by an
optical tweezer, over a wide range of pressures. They were able to measure the instantaneous velocity of a Brownian particle, not just the sloppy average you would see by eye under a microscope, called the
diffusive regime.
They were able to measure the positions of the particles on a time scale small enough to observe their
ballistic regime; namely, the regime between individual "hits" by the gas molecules.[1-2]
Of course, such data are sufficient to verify the Maxwell-Boltzmann distribution. The measurement is still indirect, but it's much better than a strict reliance on faith. The Texas experiments were aided by the fact that the fluid medium, air, was
rarefied and had a low
viscosity.
The Texas team, assisted by colleagues at the Ecole Polytechnique Fédérale de Lausanne, have since extended their observation to ballistic Brownian motion in a
liquid.[3]
This was the first measurement of Brownian motion in a liquid in the ballistic regime. A liquid is more difficult for this type of experiment, since liquid viscosities are about fifty times that of air. To analyze the Brownian motion in the liquid, they captured a single particle in an optical trap and measured its position with
sub-Angstrom spatial resolution in a 75
MHz bandwidth.[3]
The position measurement used a fast
photodetector coupled via an
optical fiber bundle, and it could resolve 20
picometers. This is about the size of a
hydrogen atom. Such measurement extremes are required, since a one micrometer silica bead in water will move a
nanometer every
microsecond.
This is predicted by the
Stokes-Einstein relation,
D = (kBT) / (6 π η r),
in which D, the
diffusion constant, is given by k
B, the
Boltzmann constant, T, the
absolute temperature, η, the
viscosity, and r, the particle radius.
After taking the particle
inertia and the
hydrodynamic effect of the fluid into account, their data were in excellent agreement with theory.[3]
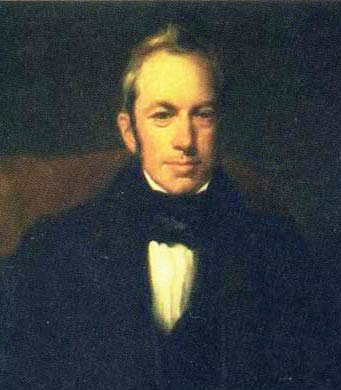
Portrait by Henry William Pickersgill (1782-1875) of the Botanist, Robert Brown, as a young man.
Brown discovered Brownian motion of particles in fluids.
(Via Wikimedia Commons))
![]()
References:
- Tongcang Li, Simon Kheifets, David Medellin and Mark G. Raizen, "Measurement of the Instantaneous Velocity of a Brownian Particle," Science, vol. 328 no. 5986 (June 25, 2010), pp. 1673-1675.
- Peter N. Pusey, "Brownian Motion Goes Ballistic," Science, vol. 332 no. 6031 (May 13, 2011), pp. 802-803.
- Rongxin Huang, Isaac Chavez, Katja M. Taute, Branimir Lukić, Sylvia Jeney, Mark G. Raizen and Ernst-Ludwig Florin, "Direct observation of the full transition from ballistic to diffusive Brownian motion in a liquid," Nature Physics, vol. 7, no. 7 (July, 2011), pp. 576-580.
- Kinetic Theory of Gases Page at HyperPhysics
Permanent Link to this article
Linked Keywords: Physics; theory; experiment; Maxwell-Boltzmann distribution; molecule; velocity; gas; pressure; physicists; Center for Nonlinear Dynamics and Department of Physics; University of Texas at Austin (Austin, Texas); Brownian motion; random; fluid; botanist; Robert Brown; microscope; pollen grain; amyloplasts; spherosome; scientist; inorganic; life-related; arXiv preprint server; Wiener process; Norbert Wiener; T.J. Sullivan; Wikimedia Commons; micrometer; silica glass bead; air; optical tweezer; diffusion; ballistic; rarefied; viscosity; liquid; Angstrom; MHz; bandwidth; photodetector; optical fiber; picometer; hydrogen atom; nanometer; microsecond; Stokes-Einstein relation; diffusion constant; Boltzmann constant; absolute temperature; viscosity; inertia; hydrodynamic.