| Tikalon Blog is now in archive mode.
An easily printed and saved version of this article, and a link
to a directory of all articles, can be found below: |
|
This article |
| Directory of all articles |
Shear Thickening
March 14, 2014
Most readers of this
blog should be familiar with the special properties of certain
corn starch-
water mixtures. This substance is sometimes called
oobleck after a similar substance described in
Bartholomew and the Oobleck, a 1949 book by
Theodor Seuss Geisel (a.k.a., Doctor Seuss).
The usual
formulation is one part water to 1.5-2 parts cornstarch, by
volume. Corn starch is
insoluble in water, so the mixture is a
suspension of fine particles in a water solution, a
colloid. This mixture is a
non-Newtonian fluid.
Simply, this means that you can easily poke your
hand into the
mixture if you do this slowly; but, if you punch the mixture, it's as hard as a
rock. You can roll the mixture into a ball with your hands, but it slumps back into a
liquid when you stop working it. There are several interesting online
video demonstrations of the various properties of Oobleck,[1] and an accessible
tutorial article.[2]
We can best explain the properties of non-Newtonian fluids by first describing a
Newtonian fluid. A Newtonian fluid has the
linear mechanical property that its
viscous stress ("drag") is
proportional to the local
strain rate. For an
isotropic fluid, the local strain rate is the rate of change of the fluid's
velocity vector as it flows
perpendicular to the shear direction. This is expressed by the
equation,
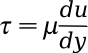
where
τ is the shear stress,
μ is the shear viscosity of the fluid, and
du/dy is the
derivative of the velocity component in the shear direction, relative to the perpendicular direction. Water is a good example of a Newtonian fluid.
The shear viscosity of a non-Newtonian fluid is not constant, and it may even be
time-dependent. The difference in mechanical properties between a Newtonian fluid and a dilitant fluid, such as Oobleck, can be seen in the figure. Oobleck can be cycled up and down the same curve; that is, the process is
reversible.
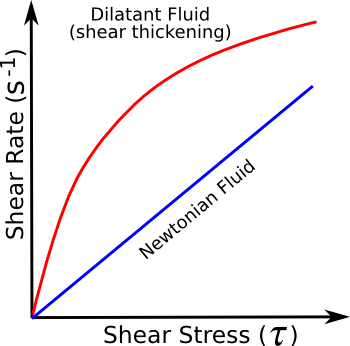
Newtonian and dilitant fluids
(Illustration by the author using Inkscape.)
Oobleck was always thought to be a non-Newtonian fluid of the dilitant type called shear-thickening; that is, it becomes thick in response to shear stress. In 2012,
Scott R. Waitukaitis and
Heinrich M. Jaeger of the
James Franck Institute and
Department of Physics, the
University of Chicago (Chicago, Illinois), performed
experiments that showed the effect was more akin to the
jamming transition of
granular media.[3-5] While shear-thickening can explain such mixtures' response to small
forces, the Chicago experiments showed why they're able to support the weight of a
human running on their
surface.
Waitukaitis and Jaeger
calculated that the material would need ten times more shear stress than it has to support a running person.That's because running generates more
compression than
shear. To prove this by experiment, they shot a 370
gram aluminum rod into a cornstarch colloid at a
meter per second and recorded the results with
high speed photography and
X-rays.[5]
The
impacting rod compressed the cornstarch particles so that they jammed against each other to form a rigid core. This is a known
phenomenon for granular materials, and such rigid cores exert an upward force sufficient to counteract applied
pressure. A movement into the cornstarch colloid of just five
centimeters forms a core to a depth of 50 centimeters.[5]
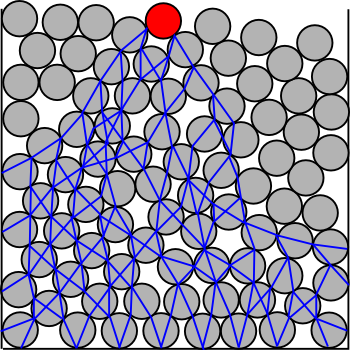
Compressive stress distribution in a granular medium.
The compressive stress is distributed to lower particles in roughly a cone-shaped core.
(Via Wikimedia Commons.)
This idea that shear-thickening mixtures have much in common with granular media has been
modeled by
researchers at the
City College of New York (CCNY, New York, New York). Their model, which included
hydrodynamic interactions and contact between the particles, showed that contact
friction is essential for having
discontinuous shear thickening.[6] Colloids with a large enough
volume fraction of particles show two states. There's a low viscosity state with few particle contacts, a high viscosity state like a jammed granular material, and a critical shear rate that transitions from one state to the other.[6]
According to the model, this is a
second-order phase transition, since the viscosity is discontinuous at the critical shear rate. The transition is reversible, since the colloid behaves like a normal liquid when the shear is removed.[7] As shown in the figure, particles become linked together above the critical shear rate, and the
lubricating liquid is not able to flow between them.[9] The particles in the colloid act as a dry, granular medium. The CCNY model accurately reproduces experimental observations.[7,9]
(left and right images via City College of New York.)[8)]
References:
- Non-Newtonian Fluid on a Speaker Cone, YouTube Video, November 26, 2008.
- Norman J. Wagner and John F. Brady, "Shear thickening in colloidal dispersions," Physics Today, vol. 62, no. 10 (October, 2009), pp. 27-32; PDF file available, here.
- Scott R. Waitukaitis and Heinrich M. Jaeger, "Impact-activated solidification of dense suspensions via dynamic jamming fronts," Nature, vol. 487, no. 7406 (July 12, 2012), pp. 205-209.
- Martin van Hecke, "Soft matter: Running on cornflour," Nature, vol. 487, no. 7406 (July 12, 2012), pp. 174-175.
- Jon Cartwright, "Cornstarch Physics Is Shear Nonsense," Science Now, July 11, 2012.
- Ryohei Seto, Romain Mari, Jeffrey F. Morris and Morton M. Denn, "Discontinuous Shear Thickening of Frictional Hard-Sphere Suspensions," Phys. Rev. Lett., vol. 111, no. 21 (November 22, 2013), Document No. 218301 [5 pages].
- Eric Brown, "Viewpoint: Friction's Role in Shear Thickening," Physics, vol. 6, no. 125 (November 18, 2013).
- CCNY Team Models Sudden Thickening of Complex Fluids, CCNY Press Release, January 16, 2014.
- Tim Wogan, "Model explains why liquid suspensions suddenly turn solid," Physics World, November 25, 2013.
Permanent Link to this article
Linked Keywords: Blog; corn starch; water; Oobleck; Bartholomew and the Oobleck; Theodor Seuss Geisel; formulation; volume; solubility; insoluble; suspension; colloid; non-Newtonian fluid; hand; mixture; rock; liquid; video; tutorial; Newtonian fluid; linearity; linear; strength of materials; mechanical property; viscous stress tensor; viscous stress; proportionality; proportional; strain rate; isotropy; isotropic; fluid; velocity vector; perpendicular; equation; derivative; time-variant system; time-dependent; reversible process; Inkscape; Scott R. Waitukaitis; Heinrich M. Jaeger; James Franck Institute; Department of Physics; University of Chicago (Chicago, Illinois); experiment; jamming transition; granular material; granular media; force; human; running; surface; calculation; compression; shear stress; gram; aluminum; rod; meter per second; high speed photography; X-rays; impact; phenomenon; pressure; centimeter; cone; Wikimedia Commons; computer simulation; model; research; City College of New York (CCNY, New York, New York); hydrodynamic; friction; continuous function; discontinuous; volume fraction; second-order phase transition; lubrication.