| Tikalon Blog is now in archive mode.
An easily printed and saved version of this article, and a link
to a directory of all articles, can be found below: |
|
This article |
| Directory of all articles |
The Birthday Problem
August 4, 2010
Today is the birthday of one of my family members. To celebrate, I'm reviewing a bit of mathematics called the "Birthday Problem." I was introduced to the Birthday Problem when I was in high school. I attended a weekly mathematics seminar, called the
Colgate Seminar, taught by a rotating corp of professors from nearby
Colgate University. The Birthday problem is an example problem that's often used with high school students. The math isn't difficult, and the result is surprising. The problem is this - how many people do you need in a room, such that it's more likely than not that two of them have the same birthday? The important piece of the problem is not that any person has a particular birthday, or any person has the same birthday as one particular person; rather, that any two people will have the same birthday. To make things simple, disregard leap years, consider just 365 days in a year, and ignore twins. Surprisingly, there was a set of twins in my seminar session.
The mathematics is quite simple. We use the principle that we can calculate the
probability of independent events happening at the same time by multiplying their separate probabilities. We start with the first pair of people, N = i and N = (i + 1). The probability that person (i + 1) has a different birthday than person i is 364/365; that is, person (i + 1) must be born on any of the remaining 364 days that are not the birthday of person i. Bringing in another person (i + 2), and comparing him with persons i and (i + 1) gives us a probability of 363/365 that his birthday differs from the previous people. Continuing the calculation
P = (364/365)(363/365)(362/365)...
or, in compact notation
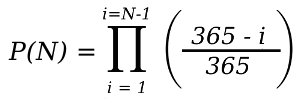
where P(N) is the probability that in a group of N people, no two will have the same birthday. Of course, what we want is (1 - P(N)), the probability that two will have the same birthday. As you can see from the table, not that many people are needed to have just a 50:50 chance. It takes just 23 people to have a 50.7% probability that two will have the same birthday.
| N | P(N) | 1 - P(N) |
| 5 | 0.97286 | 0.02714 |
| 10 | 0.88305 | 0.11695 |
| 15 | 0.74710 | 0.25290 |
| 20 | 0.58856 | 0.41144 |
| 25 | 0.43130 | 0.56870 |
| 30 | 0.29368 | 0.70632 |
| 35 | 0.18562 | 0.81438 |
| 40 | 0.10877 | 0.89123 |
| 45 | 0.05902 | 0.94098 |
| 50 | 0.02963 | 0.97037 |
OK, so we have a nice parlor trick, but is any of this useful? I mentioned
cryptographic hash functions in a
previous article (The US Cyber Command, July 14, 2010), and the concept of
hash collisions. If a hash function has just 365 elements, you can see how a generalization of the Birthday Problem shows that a collision is likely in a collection of just 23 of these elements. Of course, useful hash functions have many more elements, but the same principle applies. If your N-bit hash function can generate 2
N codes, you'll get a collision not after 2
N codes are generated, but rather after only 2
N/2 codes are generated.
There is, in fact, a so-called
birthday attack on hash functions; viz., generating multiple messages and finding a collision between an arbitrary pair of them is far easier than generating a document that has the same hash value as a particular document. For example, you may want to generate two nearly similar contracts that have the same hash value (a.k.a., digital signature), so you insert commas, extra spaces or blank lines, or use synonyms for words, until you get a collision. Then, one contract can be substituted for the other at a later time.

I mentioned my high school interest in mathematics (see the figure). I did pursue a career in a mathematically intensive field; but I didn't particularly care for mathematics instruction, so I never considered becoming a mathematician. In later life, I've rediscovered some interesting mathematics, and I'm happy that I had enough math education for me to do some independent study.
References:
- Birthday Problem page on Wikipedia.
- Birthday Problem on MathWorld.
Permanent Link to this article
Linked Keywords: Colgate Seminar; Colgate University; probability; cryptographic hash functions; hash collisions; birthday attack