Prime Walk
July 12, 2021
Humans try to find
patterns in things. As a
child in
school, I'm fairly certain that's the way that I learned
mathematics. As a
computer programmer, I find that discovering one good example on the
Internet is better than a
textbook chapter. As in most human things, the concept can be taken too far. That's why people try to find
hidden messages in the Bible. I vaguely remember the
plot of a
60s television show that has a
scientist and his followers retreat to a
cave since they are sure that a
nuclear war would occur at a specific time. The time was related to the
rising of the
constellation,
Boötes, simply because a
Russiann
scientist had misspelled
boots as
bootes in a
letter.
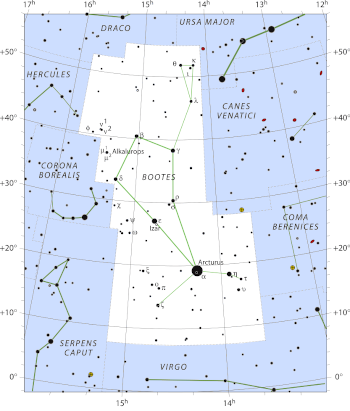
The constellation, Boötes (The Plowman), is not well known, since it is not among the twelve constellations of the Zodiac. However, it is among the 48 constellations described by Ptolemy (c.100-c.170), and it is one of the 88 modern constellations.
Arcturus (α-Boötes), which is 36.7 light-years from Earth, is the fourth-brightest star in the night sky (apparent magnitude, -0.05)
(Modified Wikimedia Commons image by Roger Sinnott & Rick Fienberg/the IAU/Sky & Telescope magazine. Click for larger image.)
In 1932,
American herpetologist,
Laurence Monroe Klauber (1883-1968) presented a
paper to the
Mathematical Association of America in which he showed the
geometric regularity in the distribution of the
prime numbers when the
natural numbers were arranged in a
triangle (see figure).
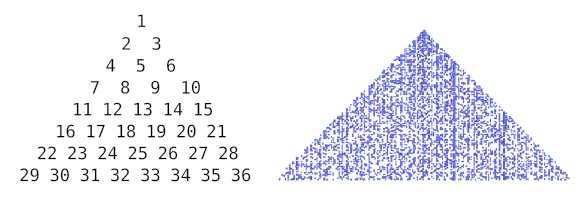
Klauber's triangular representation of the prime numbers. The plot on the right, generated using the Python program in ref. 1, highlights the primes as colored points.[1] (Klauber.py source here. Click for larger image.)
Klauber noted that this
phenomenon was related to
prime-generating polynomials, such as the one devised by
Euler. In a 1772 letter to
Johann Bernoulli, Euler mentioned that the
function,
f(n) = n2 + n + 41
has prime values for 0 ≤ n ≤ 39.[2-3] This function fails at n = 40, which gives f(n) = 1681, but it gives primes with a high
frequency for larger n.
In 1963,
Polish-American
physicist,
Stanisław Ulam (1909-1984), independently discovered a similar phenomenon on a
square lattice of numbers that's now known as the
Ulam spiral (see figure). Ulam made this discovery while
doodling during
presentation of "a long and very boring paper" at a
scientific conference, something that many scientists have experienced.
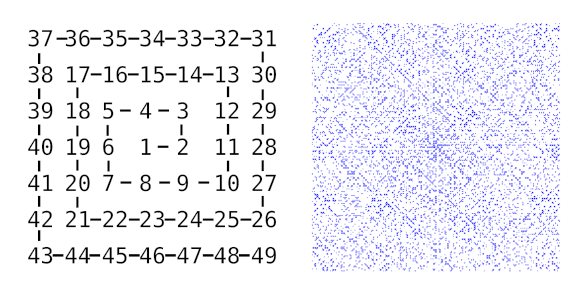
The Ulam spiral representation of the prime numbers. The plot was generated using the Python program in ref. 4.[4] (Ulam.py source here. Click for larger image.)
The Ulam spiral was
popularized by
Martin Gardner in his March, 1964,
Mathematical Games column in
Scientific American. Ulam, who had an early interest in
computers, and his
colleagues used the
Los Alamos MANIAC II to produce an spiral of about 100,000 points, and they investigated some prime-rich and prime-poor lines.
An international team of scientists was inspired by the Ulam spiral to create a novel
random walk in
two-dimensions that they call a
prime walk. The team had members from the
Czech Technical University in Prague (Prague, Czech Republic), the
Universidade de São Paulo (São Paulo, Brazil), the
Universidad del País Vasco (Leioa, Spain), the
National Kapodistrian University of Athens (Athens, Greece), and the
University of Iceland (Reykjavík, Iceland). Their study was published recently on
arXiv, and later in
Physical Review E.[5]
A random walk on a square lattice can be created by having a point trace a path by moving
randomly up, down, left, or right. The prime walk has instead the
following rules based on the idea that (aside from the prime numbers 2 and 5) the last
digits of prime numbers are 1, 3, 7 and 9:
• The starting point at (0, 0) is given the value N = 1.
• At the current point (x, y), find N + 1.
• If N + 1 is not a prime, don't move. If it is a prime, assign N + 1 to a new position, as follows.
• If N + 1 is a prime and its last digit is 1, move up; i.e., (x, y) -> (x, y + 1).
• If N + 1 is a prime and its last digit is 3, move down; i.e., (x, y) -> (x, y − 1).
• If N + 1 is a prime and its last digit is 7, move left; i.e., (x, y) -> (x − 1, y).
• If N + 1 is a prime and its last digit is 9, move right; i.e., (x, y) -> (x + 1, y).
A
computation can track how many times a lattice point has been visited, allowing the
visualization of the prime walk in the following figure.
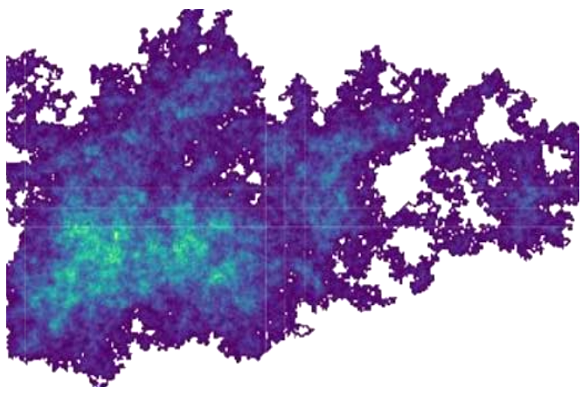
Visualization of the prime walk. The shading shows how often a lattice point was visited. (Portion of fig.1 of ref. 5.[5])
The prime walk has some interesting properties, one of which is that the covered
area is 1/10 the number of primes. Furthermore, the first digit of the maximum number of cell visits follows
Benford's law (see figure).[5]
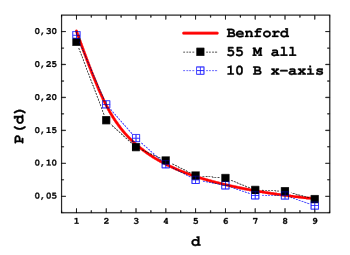
Benford's law for the prime walk. This is a histogram of the leading digits of the maximum number of cell visits for walks to length 5.5 x 107 (black squares).
The blue squares are for values on the x-axis for walks up to 109 steps. Benford's law is shown by the red curve.
(Fig. 6 of ref. 5.[5])
References:
- The Klauber Triangle, Article by 'christian,' September 6, 2016, on scipython.com blog,
- Justin DeBenedetto and Jeremy Rouse, "A 60,000 digit prime number of the form x2 + x + 41," arXiv, July 31, 2012.
- Leonhard Euler, "Extrait d'un lettre de M. Euler le pere à M. Bernoulli concernant le Mémoire imprimé parmi ceux de 1771" (Extract of a letter from the father Mr. Euler to Mr. Bernoulli, concerning the Mémoire published among those of 1771), Enestrom Number 461.
- The Ulam Spiral, Article by 'christian,' September 2, 2016, on scipython.com blog.
- Alberto Fraile, Osame Kinouchi, Prashant Dwivedi, Roberto Martínez, Theophanes E. Raptis, and Daniel Fernández, "Prime numbers and random walks in a square grid," Phys. Rev. E, vol. 104, no. 5 (November 15, 2021), Article no. 054114, DOI: https://doi.org/10.1103/PhysRevE.104.054114. Also avaiable at ArXiv.
Linked Keywords: Human; pattern; child; grammar school; mathematics; computer programmer; Internet; textbook; chapter (books); Bible code; hidden messages in the Bible; plot (narrative); 1960s; television program; television show; scientist; cave; nuclear warfare; nuclear war; heliacal rising; rising; constellation; Boötes; Russia; Russian; scientist; boot; letter (message); The Plowman; Zodiac; Ptolemy (c.100-c.170); Arcturus (α-Boötes); light-year; Earth; star; night sky; apparent magnitude; Wikimedia Common; America; American; herpetology; herpetologist; Laurence Monroe Klauber (1883-1968); academic publishing; paper; Mathematical Association of America; geometry; geometric; prime number; natural number; triangle; triangular; visualization (graphics); representation; plot (graphics); Python (programming language); computer program; Klauber.py source; phenomenon; prime-generating polynomial; Leonhard Euler; Johann Bernoulli; function (mathematics); frequency; Poland; Polish; physicist; Stanisław Ulam (1909-1984); square lattice; Ulam spiral; doodle; doodling; presentation; scientific conference; Ulam.py source; popular science; popularize; Martin Gardner; Mathematical Games column; Scientific American; computer; colleague; Los Alamos National Laboratory; MANIAC II; random walk; two-dimensional space; Czech Technical University in Prague (Prague, Czech Republic); Universidade de São Paulo (São Paulo, Brazil); Universidad del País Vasco (Leioa, Spain); National Kapodistrian University of Athens (Athens, Greece); University of Iceland (Reykjavík, Iceland); arXiv; randomness; random; algorithm; rules; numerical digit">digit; computation; Visualization; lattice graph; lattice point; area; Benford's law; histogram.