Polymaths
November 30, 2020
There's an interesting generalization about
specialists, as follows:
"An expert knows more and more about less and less until he or she knows everything about nothing."
This
saying is apparently a
comedic amplification of a shorter one used by
William Warde Fowler (1847-1921) of
Oxford University in a 1911
book review in the
journal,
Review of Theology & Philosophy.[1] The
antithesis of a specialist is a
polymath. When I first heard the term, polymath, as a young
student, I though it was the name for a field of
geometry concerned with
polygons; however, a polymath is a person with extensive knowledge in many fields.
A casual look at the home page of
arXiv, the
physics,
mathematics, and related
sciences preprint web server, illustrates the many physics specialities, as follows:
• Astrophysics (Including Astrophysics of Galaxies; Cosmology and Nongalactic Astrophysics; Earth and Planetary Astrophysics; High Energy Astrophysical Phenomena; Instrumentation and Methods for Astrophysics; Solar and Stellar Astrophysics)
• Condensed Matter (Including Disordered Systems and Neural Networks; Materials Science; Mesoscale and Nanoscale Physics; Other Condensed Matter; Quantum Gases; Soft Condensed Matter; Statistical Mechanics; Strongly Correlated Electrons; Superconductivity)
• General Relativity and Quantum Cosmology
• High Energy Physics (Including High Energy Physics-Experiment
High Energy Physics-Lattice
High Energy Physics-Phenomenology
High Energy Physics-Theory)
• Mathematical Physics
• Nonlinear Sciences (Including Adaptation and Self-Organizing Systems; Cellular Automata and Lattice Gases; Chaotic Dynamics; Exactly Solvable and Integrable Systems; Pattern Formation and Solitons)
• Nuclear Experiment
• Nuclear Theory
• Physics (Including Accelerator Physics; Applied Physics; Atmospheric and Oceanic Physics; Atomic and Molecular Clusters; Atomic Physics; Biological Physics; Chemical Physics; Classical Physics; Computational Physics; Data Analysis, Statistics and Probability; Fluid Dynamics; General Physics; Geophysics; History and Philosophy of Physics; Instrumentation and Detectors; Medical Physics; Optics; Physics and Society; Physics Education; Plasma Physics; Popular Physics; Space Physics)
• Quantum Physics

A milestone in physics specialization was reached in 1970 when Physical Review, the pre-eminent physics journal published since 1893, split into four journals; namely, A (Atomic, Molecular, and Optical Physics), B (Condensed Matter, Structure, Phase Transitions, Nonordered Systems, Magnetism, Superconductivity, Superfluidity, Electronic Structure, Semiconductors, Surfaces, Low Dimensions)), C (Nuclear Physics), and D ((Particles, Fields, Gravitation, and Cosmology)).
An additional journal, E (Statistical, Nonlinear, and Soft Matter Physics), was added in 1993.
Annual online subscriptions are presently $70 for each.
(Modified Wikimedia Commons image by Inductiveload.)
My favorite polymath is
Carl Friedrich Gauss (1777-1855), who made significant contributions to mathematics and many fields of physics. In common with many polymaths, Gauss's
mental abilities were apparent at a very early age, as an interesting
anecdote from the
history of mathematics illustrates.[2] As the story goes, Gauss was an eight year old
elementary school student who was given a lengthy
mathematics problem by his
teacher. It's a common
tactic for teachers to assign such "busy work" problems when they need time to
grade homework or
tests.
The assignment, sure to take the students quite a lot of time, was to
add together all the
numbers from one to a hundred. Gauss immediately arrived at the correct answer, 5050, with no written
calculation. Gauss had realized that it was possible to pair the numbers, 1 with 99, 2 with 98, etc., to give you 49 sums of a hundred each. Adding the additional 100 and 50 immediately gave the answer, 5050.[2] There's a general
formula for calculating the sum of such a
XX up to the number
n,
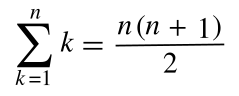
This gives us Gauss' answer when
n = 100.

Carl Friedrich Gauss (1777-1855).
Gauss has a plethora of things named after him, including a unit of magnetism, the gauss, that's been superseded by the tesla.
As I wrote in an earlier article (Great Circle Routes, June 25, 2018), Gauss did an experiment in the 1820s to determine whether space was curved; that is, non-Euclidean.
He used his era's version of a laser theodolite, called a heliotrope, to survey a triangle between three mountains - Brocken, Hohenhagen, and Inselberg.
This triangle had sides of length 69, 85 and 107 kilometers, but even such a large triangle has the now known difference in the sum of angles from 180 degrees of just 0.1 picoradians.
(An 1840 oil portrait by the danish painter Christian Albrecht Jensen (1792-1870), via Wikimedia Commons)
Fourier transforms are ubiquitous in
signal analysis, and they are most importantly used to
calculate the
frequency spectrum of
time-series signals. Everyone desires more speed in calculations, and the Fourier transform was improved by an algorithm called the
Fast Fourier transform (FFT), the first such example of which was the
Cooley–Tukey FFT algorithm, named after its creators,
James Cooley (1926-2016) and
John Tukey (1915-2000).[3]
Interestingly, the mathematics behind the Cooley-Tukey FFT was anticipated by Gauss around 1805 and published in 1866 after his death.[4-5] Gauss developed this mathematics in calculating the
orbits of the
asteroids,
Pallas and
Juno. This work of Gauss even predated that of
Joseph Fourier (1768-1830), who published preliminary results in his 1807
Mémoire sur la propagation de la chaleur dans les corps solides (Treatise on the propagation of heat in solid bodies), with a more complete treatment in his
Théorie analytique de la chaleur (Analytical theory of heat) in 1822. Fourier did not know of Gauss' work, since it was only published in 1866.
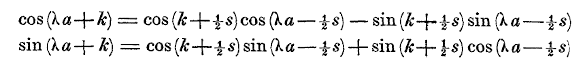
A trigonometric identity from the paper of Carl Friedrich Gauss in the section containing mathematics relevant to the Fourier transform. (Via the University of Göttingen.[4])
Author and
journalist,
Andrew Robinson, has published a review of the recent
book, "The Polymath: A Cultural History from
Leonardo da Vinci to
Susan Sontag," by
Peter Burke (b. 1937), an
emeritus professor of
cultural history at
Cambridge University.[6-7] The
appendix to Burke's book lists 500 "western polymaths," among whom are counted
Charles Darwin,
Alan Turing,
Linus Pauling, and
Thomas Young.

Linus Pauling graciously autographed a reprint of one of his papers that he sent to me. Like Pauling, I also published a paper on the 57Fe isotope of iron.[8]
The
myriad interests of da Vinci are known to most people. However, Thomas Young, who was regarded as the greatest polymath since da Vinci, is known mostly to physicists; and, then, just for his famous
double slit experiment that demonstrated the
wave nature of light. Young's
tombstone at
Westminster Abbey remembers his being "eminent in almost every department of human learning."[6]
Another of Young's accomplishments was in his initial
deciphering of the text of the
Rosetta Stone as a
clue to understanding
Egyptian hieroglyphics. Burke identifies the principal
characteristics of polymaths as "unusual powers of
concentration,
capacious memory,
speed,
imagination,
restlessness,
industriousness, and
obsession with not wasting time."[6] These characteristics likely arise during a person's early years; so, I don't think polymath
coaching of adults would ever work.
References:
- A Specialist Knows More and More About Less and Less, Quote Investigator.
- Clever Carl, NRICH team of the Millennium Mathematics Project, February, 2011.
- J.W. Cooley and J.W. Tukey, "An algorithm for the machine calculation of complex Fourier," Math. Comput., vol. 19 (1965), pp. 297-301. A PDF file is available here.
- Carl Friedrich Gauss, "Theoria interpolationis methodo nova tractata", Werke, Band 3, Königliche Gesellschaft der Wissenschaften, Göttingen, 1866), pp. 265-327 (Via the University of Göttingen.
- James W. Cooley and John W.Tukey, "On the Origin and Publication of the FFT Paper," Citation Classics, Current Contents, vol. 33, nos. 51-52 (December 20-27, 1993), pp. 8-9.
- Andrew Robinson, "A history of insatiable intellectuals," Science, vol. 369, no. 6507 (August 28, 2020), p. 1064, DOI: 10.1126/science.abb7546
- Peter Burke, "The Polymath: A Cultural History from Leonardo da Vinci to Susan Sontag, Yale University Press, September 8, 2020, 352 pp. (Via Amazon).
- D.M. Gualtieri, W. Lavender and S. Ruby, 57Fe-YIG: Narrow Xray Linewidth Epitaxial Layers on Gd3Ga5O12, J. Appl. Phys, vol. 63, no. 8 (1988), pp. 3795-3797, https://doi.org/10.1063/1.340617.
Linked Keywords: Expert; specialist; saying; comedy; comedic; William Warde Fowler (1847-1921); University of Oxford; Oxford University; book review; academic journal; antithesis; polymath; student; geometry; polygon; arXiv; physics; mathematics; sciences; preprint; web server; Astrophysics; Astrophysics of Galaxies; Cosmology and Nongalactic Astrophysics; Earth and Planetary Astrophysics; High Energy Astrophysical Phenomena; Instrumentation and Methods for Astrophysics; Solar and Stellar Astrophysics; Condensed Matter; Disordered Systems and Neural Networks; Materials Science; Mesoscale and Nanoscale Physics; Other Condensed Matter; Quantum Gases; Soft Condensed Matter; Statistical Mechanics; Strongly Correlated Electrons; Superconductivity; General Relativity and Quantum Cosmology; High Energy Physics-Experiment; High Energy Physics-Lattice; High Energy Physics-Phenomenology; High Energy Physics-Theory; Mathematical Physics; Nonlinear Sciences; Adaptation and Self-Organizing Systems; Cellular Automata and Lattice Gases; Chaotic Dynamics; Exactly Solvable and Integrable Systems; Pattern Formation and Solitons; Nuclear Experiment; Nuclear Theory; Physics; Accelerator Physics; Applied Physics; Atmospheric and Oceanic Physics; Atomic and Molecular Clusters; Atomic Physics; Biological Physics; Chemical Physics; Classical Physics; Computational Physics; Data Analysis, Statistics and Probability; Fluid Dynamics; General Physics; Geophysics; History and Philosophy of Physics; Instrumentation and Detectors; Medical Physics; Optics; Physics and Society; Physics Education; Plasma Physics; Popular Physics; Space Physics; Quantum Physics; milestone; academic specialization; Physical Review; scientific journal; atom; Atomic; molecule; Molecular; optics; Optical; condensed matter physics; Condensed Matter; crystal structure; Structure; Phase Transitions; order and disorder (physics); Nonordered Systems; Magnetism; Superconductivity; Superfluidity; energy level; Electronic Structure; Semiconductors; surface states; Surfaces; Low Dimensions; Nuclear Physics; elementary particle; Particles; field (physics); Fields; Gravitation; physical cosmology; Cosmology; statistical_mechanics; Statistical; nonlinear system; Nonlinear; Soft Matter; subscription; Wikimedia Commons; User:Inductiveload; Carl Friedrich Gauss (1777-1855); thought; mental; anecdote; history of mathematics; elementary school; mathematics problem; teacher; tactic (method); grading in education; grade; homework; test (assessment); addition; add; natural number; calculation; formula; series (mathematics); plethora; units of measurement; magnetism; gauss; tesla; experiment; spacetime; space; curvature of space; Euclidean space; non-Euclidean; laser; theodolite; heliotrope (instrument); surveying; survey; triangle; mountain; Brocken; Hoher Hagen (Dransfeld); Hohenhagen; Gro%C3%9Fer Inselsberg; Inselberg; kilometer; angle; picoradian; Christian Albrecht Jensen (1792-1870); Fourier transform; signal processing; signal analysis; calculation; calculate; frequency spectrum; time-series; Fast Fourier transform (FFT); Cooley–Tukey FFT algorithm; James Cooley (1926-2016); John Tukey (1915-2000); orbit; asteroid; 2 Pallas; 3 Juno; Joseph Fourier (1768-1830); Mémoire sur la propagation de la chaleur dans les corps solides (Treatise on the propagation of heat in solid bodies); Théorie analytique de la chaleur (Analytical theory of heat); trigonometry; trigonometric; identity (mathematics); University of Göttingen; author; journalist; Andrew Robinson; book; Leonardo da Vinci; Susan Sontag; Peter Burke (b. 1937); emeritus professor; cultural history; University of Cambridge; Cambridge University; addendum; appendix; Charles Darwin; Alan Turing; Linus Pauling; Thomas Young (scientist); autograph; autographed; reprint; 57Fe isotope of iron; myriad; double slit experiment; electromagnetic radiation; wave nature of light; headstone; tombstone; Westminster Abbey; decipherment; deciphering; Rosetta Stone; clue; Egyptian hieroglyphics; trait; characteristic; attentional control; concentration; capacious; memory; speed; imagination; stimulation; restlessness; diligence; industriousness; fixation (psychology); obsession; coaching.