| Tikalon Blog is now in archive mode.
An easily printed and saved version of this article, and a link
to a directory of all articles, can be found below: |
|
This article |
| Directory of all articles |
Armstrong Numbers
November 2, 2020
Some believe that
vanity is more often found in
women than
men, but the
mythological example of vanity is the
male character,
Narcissus (Νάρκισσος). Narcissus was a
hunter, known for his
beauty and vanity, who was
punished by the
god,
Nemesis. Nemesis caused Narcissus to fall in
love with his own
reflection in a
pool of water. Our
word,
narcissism, comes from this
myth.
Narcissus, as drawn by Oliver Herford from "An alphabet of celebrities," 1899.
In this drawing, Narcissus is admiring a daffodil, formally known as a Narcissus.
Every time I hear the word, "vanity," I think of the 1972 song, "You're So Vain," by Carly Simon.
(Portion of a Wikimedia Commons image from Project Gutenberg)
Physicists and
mathematicians enjoy giving things unusual names. In physics, we have
elementary particles with
charm, and others that are just
strange. In mathematics, there's a
number series known as the
narcissistic numbers, more formally known as the
Armstrong numbers. This sequence is simply defined as m-
digit natural numbers equal to
sum of the m-th
powers of their digits. For example,
153 = 13 + 53 + 33
8208 = 84 + 24 + 04 + 84
4210818 = 47 + 27 + 17 + 07 + 87 + 17 + 87
This is a
finite sequence of just 88 elements, the last of which being
115132219018763992565095597973971522401. It could have been called the
piano sequence, since a piano has 88
keys, but that might have been confusing, since there's a famous mathematician named
Peano. The first few numbers are
1,
2,
3,
4,
5,
6,
7,
8,
9,
153,
370,
371,
407,
1634,
8208,
9474,
54748,
92727,
93084,
548834,
1741725,
4210818,
9800817,
9926315,
24678050,
24678051, and
88593477. Eight of its members end in
zero, which ensures that their
successors are just one greater.
Although
pi can be
computed to many digits using a
personal computer, the last Armstrong number needs something close to a
supercomputer. I modified a
code snippet found on the
Internet[3] to calculate the Armstrong numbers up to
n(32) = 4679307774. You can find my
C programming language source code here. As can be seen in the figure, the computation time appears to be
linear in
n. On my modest
dual core 3600
MHz Intel i3-4160 64-bit Linux computer with 8
gigabytes of
memory, it took an
hour to calculate
n(32), so
n(88) is clearly impossible on a standard PC. However, harnessing the
computing power of one, or more,
GPUs might be useful.
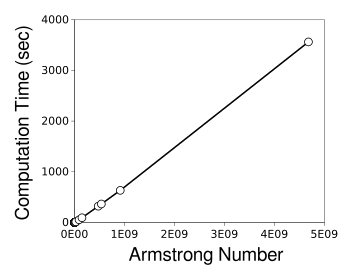
Computation time for Armstrong numbers on a personal computer having a dual core 3600 MHz Intel i3-4160 64-bit Linux computer with 8 gigabytes of memory.
My Raspberry Pi Model 4B is a factor of 3.6 times slower.
(Graphed using Gnumeric. Click for larger image.)
If we look beyond our
ten-finger mindset, we see that Armstrong numbers exist in other
number bases, such as
base-8 (octal). The number,
432, is
660 in base-8, so we have,
6608 = 63 + 63 + 03
A related sequence, if you're willing to call two numbers a sequence, are the
Münchausen numbers, which are the two numbers equal to the sum of their digits raised to the digit's power. These numbers, named after a character in a
1943 film, are 1 and 3435,[4-5]
1 = 11
3435 = 33 + 44 +33 +55 = 27 + 256 + 27 + 3125
If we allow
zero to the power of zero to be equal to zero, 0
0 = 0, as opposed to 0
0 = 1, we can add
0 and
438579088 to the list.[4-5]
Why are the numbers called Armstrong numbers? They were apparently the result of a
homework assignment for a 1966 class in
Fortran (at that time, called FORTRAN) at the
University of Rochester (Rochester, New York) taught by M.F. Armstrong.[6]
An Armstrong of a different kind.
Edwin Armstrong (1890-1954) was the inventor of FM radio and the superheterodyne radio receiver.
Significant inventions are often coveted by others, as the history of Alexander Graham Bell's telephone and the laser has shown. Armstrong's FM radio principle was coveted by RCA, which gave him no end of troubles, and this was apparently one cause of Armstrong's suicide.
Armstrong was one of the most prolific and influential inventors in radio, having more than fifty patents in his name.
(Armstrong, circa 1954, in a Wikimedia Commons image.)
References:
- Armstrong (or pluperfect, or Plus Perfect, or narcissistic) numbers (A005188), The On-Line Encyclopedia of Integer Sequences.
- Eric W. Weisstein, "Narcissistic Number," From MathWorld--A Wolfram Web Resource.
- Program for Armstrong Numbers - GeeksforGeeks.
- A variant of Munchausen numbers (A046253), The On-Line Encyclopedia of Integer Sequences.
- Eric W. Weisstein, "Münchhausen Number," From MathWorld--A Wolfram Web Resource
- Henk Koppelaar and Peyman Nasehpour, "On Hardy's Apology Numbers," arXiv, August 18, 2020.
Linked Keywords: Vanity; women; men; mythology; mythological; male; character (arts); Narcissus (mythology); hunting; hunter; beauty; punishment; punished; Greek mythology; god; Nemesis (mythology); love; reflection (physics); stream pool; pool of water; word; narcissism; myth; alphabet; celebrity; celebrities; drawing; daffodil; Narcissus (plant); song; You're So Vain; Carly Simon; Wikimedia Commons; Project Gutenberg; physicist; mathematician; elementary particle; charm quark; strange quark; series (mathematics); number series; A005188; narcissistic numbers; Armstrong numbers; numerical digit; natural number; addition; sum; exponentiation; power; infinity; finite; series (mathematics); sequence; piano; musical keyboard; keys; Giuseppe Peano; zero; successor ordinal; pi; computation; compute; personal computer; supercomputer; source code; Internet; C programming language; Armstrong.c; linear function; multi-core processor; dual core; hertz; MHz; Intel; i3-4160; 64-bit; Linux; gigabyte; dynamic random-access memory; hour; FLOPS; computing power; graphics processing unit; GPU; Computation time for Armstrong numbers on a personal computer; Raspberry Pi; Model 4B; Gnumeric; decimal; ten-finger mindset; radix; number base; A010354; base-8 (octal); A046253; Münchausen numbers; M%C3%BCnchhausen (1943 film); zero to the power of zero; homework assignment; Fortran; University of Rochester (Rochester, New York); Edwin Armstrong (1890-1954); invention; inventor; frequency modulation; FM radio; superheterodyne radio receiver; covet; Alexander Graham Bell; telephone; laser; RCA; suicide; patent.