Ultra-High Q
July 23, 2018
As I wrote in an
earlier article (Trilobite Sex, March 13, 2017),
biochemist and prolific
science fiction author,
Isaac Asimov (1920-1992), had a simple test to determine whether or not a person was a
scientist. It was how they interpreted the word,
unionized. Non-scientists will invariably think of a
trade union, while scientists will think of a
neutral atom; that is, an atom that's not
ionized.
I've developed a similar test for
electrical engineers (and some
physicists) based on the definition of
Q. About the only
Q that persons not knowledgeable in electrical engineering recollect is
Q from the
James Bond films. "Q" is Bond's
quartermaster, the person responsible for the supply of his high-tech
spy gear, such as the early version of
vehicle tracking that appeared in the 1964 film,
Goldfinger.
Electrical engineers think of a different
Q, the
quality factor that relates the
bandwidth to the
frequency of a
tuned circuit, or the
damping of an excited
resonator. Combination of an
inductor,
capacitor, and
resistor in either a
series or
parallel LCR circuit provides an
electrical resonance that can be used to produce
electronic oscillators and
filters. A simple
AM radio circuit consists of an oscillator based on a parallel LCR combination with a
variable capacitor for tuning, and several other parallel LCR stages for
intermediate frequency filtering.

Series (left) and parallel (right) inductance-capacitance-resistance (LCR) tuned circuits. In each case, the resistance produces energy loss that dampens the resonance amplitude. In the series circuit, the signal source is an ideal voltage source having zero resistance. In the patallel circuit, the signal source is an ideal current source that has infinite resistance. (Created using Inkscape.)
The resistance in these circuits determines the extent to which the stored energy is dissipated and the amplitude of the resonance is damped. The quality factor,
Q, is a measure of how well the circuit keeps its stored energy. For a series circuit, the Q is given by
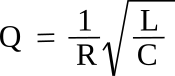
where the inductance
L is given in
henrys, the capacitance
C is given in
farads, and the resistance
R is given in
ohms. Not surprisingly, the Q of a parallel LCR circuit is the
inverse of this; viz.,
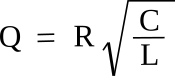
A high Q-factor indicates a sharp resonance. As shown in the following figure, the bandwidth at the
half-power points on the amplitude
vs frequency curve is related to
Q and the resonance frequency
fc. The actual half-power value is 3.0103
dB, but few
instruments can measure that accurately, and few engineers would even care.
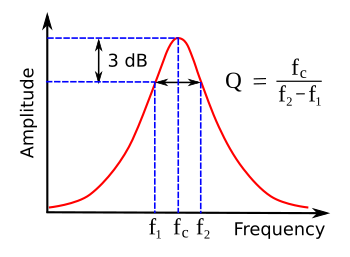
Q related to the 3-dB bandwidth.
The bandwidth is arbitrarily taken at the half-power (3 dB) point, which is a convenient measure.
Q is reciprocally related to bandwith, with a high Q indicating a narrow bandwidth.
(Created using Inkscape.)
While it's difficult to get a Q much higher than 100 in an LCR circuit,
quartz crystals routinely achieve Q-values of 10,000 or more. Since energy loss in quartz crystal
wafers is strongly influenced by their mounting, the attached
electrodes, and
acoustic coupling to
air, crystals with high-Q are
convex in shape to keep their energy away from the edge mounts, have light attachment
wires, and are enclosed in a
vacuum. In this way, Q-values in excess of 100,000 can be achieved. Quartz crystals are used to make
crystal filters with a sharply-defined
passband for
radio receivers.
All this is predicated on the fact that the quartz crystal itself has few
lattice defects. Originally, quartz crystals for resonators were
mined as
minerals.
Herkimer, New York is one source of large, clear crystals of quartz, where they are found in
dolomite rock. Quartz crystals are impressive in appearance, since they are large and
double-terminated, exhibiting
facets all around.
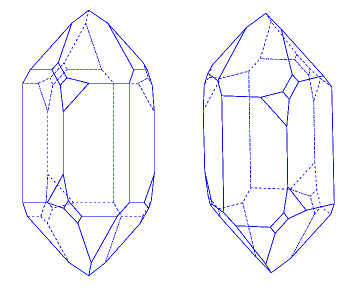
Crystal facets of quartz.
Quartz grows as left- and right-handed crystals, as shown.
(Left image and right image by "strickja," via Via Wikimedia Commons, modified.)
Laboratory-grown quartz crystals are produced by the same
hydrothermal crystallization that forms them in
nature.
Silica, dissolved in hot
water, is transported to a
seed crystal to allow the crystal to grow to a larger size. The mining of natural quartz for electronic resonators essentially ended in the
mid-20th century when
manufactured quartz became available. The
industrial synthesis of quartz was developed at
Bell Labs by A. C. Walker and Ernie Buehler.[1-2]
Quartz crystals have become
commodity items, but modern
integrated circuit technology has given us an alternative in a new class of resonators,
microelectromechanical system (MEMS) oscillators. These are essentially miniaturized
mechanical structures, some of which exhibit extremely high-Q. The Q-factor of LCR circuits is easily calculated from the component values, and measurement of the resonant frequency and bandwidth of quartz and MEMS resonators can give
Q by a different route, but there's a more fundamental technique of measuring the damping itself. If we set a device into resonance by "
pinging" it with a quick
voltage pulse, the resonator will ring with a decaying
sine wave according to the well-known
function
A(t) = Ao e-λt cos(t)
where
A(t) is the amplitude as a function of time,
Ao is the initial amplitude, and lambda (
λ), called the
log decrement, sets the rate of decay. The degree of decay, or damping, is related to Q as 2π(Energy Stored/Energy Lost per cycle).
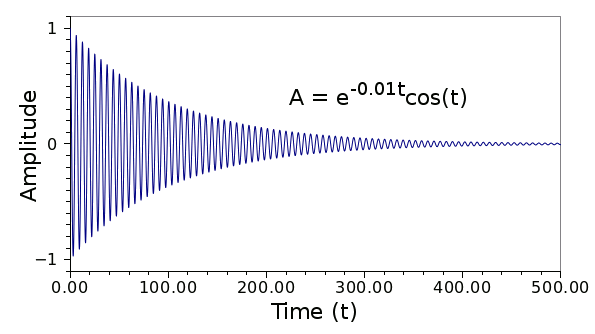
Amplitude of a damped harmonic oscillator. In this case, the log decrement is 0.01, giving the equation shown on the plot. (Graph created using Gnumeric.)
A Q-factor of 100,000 is impressive, representing a 10 Hz bandwidth at 1
MHz, but how high a
Q can a resonator have? That's the problem tackled by a team of scientists from the
École Polytechnique Fédérale de Lausanne (Lausanne, Switzerland) and
IBM Research–Zurich (Rüschlikon, Switzerland).[3-5] By
engineering stress in the resonant
ribbon of a micromechanical oscillator, they achieved a Q value of 800,000,000.[5]
It's possible to enhance the performance of devices by the addition of stress or
strain into their
materials. For example, mechanical stress in
silicon produces
transistors operable at higher
frequencies.[3] Stress in
semiconductor material used in
solar cells results in a higher
electron mobility that leads to greater
efficiency.[4] Engineering stress into a resonator would increase the Q-factor if it diminishes damping and reduces the energy lost per resonant cycle.[5]
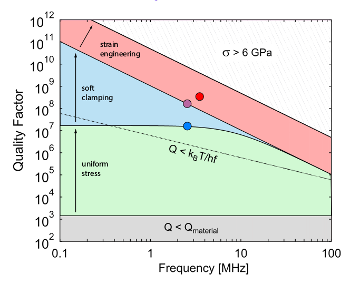
How stress and its resultant strain affects resonator quality Q.
(Fig. 1b of ref. 4. Click for larger image.)[4]
The research team was able to enhance the Q-value of a
silicon nitride (Si
3N
4) nanobeam by
etching it with a
spatially non-uniform
photonic crystal pattern.[4] This allowed a co-localization of strain and
flexural motion in the nanobeam.[3] The structure also produced
dissipation dilution in which the
stiffness of a material is effectively increased without adding loss.[4] This study builds on previous work with
membrane resonators in which a periodic pattern of holes was punched into a thin membrane, leaving just a small central island intact.[6] The hole pattern isolated the membrane resonator from its mounting so it behaved as if it were in a vacuum, and this increased the Q-value of the membrane.[5-6]
These high Q-values were measured by the ringdown technique, which showed Q-factors as high as 800 million, and the product of Q and frequency exceeding 10
15.[3-4] There are quite a few applications for such high-Q resonators, including measurement of
atto-
newton forces.[4]

Width and stress profile of a resonator ribbon etched with 60 unit cells. (Fig. 2b of ref. 4. Click for larger image.)[4]
References:
- A. C. Walker, "Hydrothermal Synthesis of Quartz Crystals," Journal of the American Ceramic Society, vol. 36, no. 8 (August, 1953), pp. 250-256.
- Ernest Buehler, "Method of growing quartz crystals," US Patent No. 2,785,058, March 12, 1957.
- Amir H. Ghadimi, Sergey A. Fedorov, Nils J. Engelsen, Mohammad J. Bereyhi, Ryan Schilling, Dalziel J. Wilson, and Tobias J. Kippenberg, "Elastic strain engineering for ultralow mechanical dissipation," Science, vol. 360, no.6390 (May 18, 2018), pp. 764-768, DOI: 10.1126/science.aar6939.
- Amir H. Ghadimi, Sergey A. Fedorov, Nils J. Engelsen, Mohammad J. Bereyhi, Ryan Schilling, Dalziel J. Wilson, and Tobias J. Kippenberg, "Strain engineering for ultra-coherent nanomechanical oscillators," arXiv, November 16, 2017.
- Alexander Eichler, "Perspective, Quantum Materials, Little is lost," Science, vol. 360, no.6390 (May 18, 2018), pp. 706-707, DOI: 10.1126/science.aat1983.
- Yeghishe Tsaturyan, Andreas Barg, Eugene S. Polzik, and Albert Schliesser, "Ultracoherent nanomechanical resonators via soft clamping and dissipation dilution," Nature Nanotechnology, vol. 12 (June 12, 2017), pp. 776-783, https://doi.org/10.1038/nnano.2017.101. Also at arXiv.
Linked Keywords: Biochemistry; biochemist; science fiction; author; Isaac Asimov (1920-1992); scientist; trade union; neutral particle; atom; ionization; ionized; electrical engineering; electrical engineer; physicist; Q; James Bond; film; quartermaster; espionage; spy; vehicle tracking; Goldfinger; Q factor; quality factor; bandwidth; frequency; LC circuit; tuned circuit; damping ratio; damping; resonator; inductor; capacitor; resistors; series LC circuit; parallel LC circuit; LCR circuit; electrical resonance; electronic oscillators; electronic filter; AM broadcasting; AM radio; electronic circuit; variable capacitor; intermediate frequency; inductance-capacitance-resistance (LCR) tuned circuit; energy; amplitude; ideal voltage source; ideal current source; Inkscape; henry; farad; ohm; multiplicative inverse; half-power point; decibel; dB; measuring instrument; 3 dB point; Wikimedia Commons; quartz crystal; wafer (electronics); electrode; acoustic; atmosphere of Earth; air; convex; wire; vacuum; crystal filter; passband; radio receiver; crystallographic defect; lattice defect; mining; mined; mineral; Herkimer, New York; dolomite rock; double terminated crystal; facet; crystal; chirality; left- and right-handed; crystal growth; Laboratory-grown; hydrothermal synthesis; hydrothermal crystallization; nature; silicon dioxide; silica; water; seed crystal; mid-20th century; manufactured; industry; industrial; chemical synthesis; Bell Labs; commodity item; integrated circuit; technology; microelectromechanical system (MEMS); oscillators; classical mechanics; mechanical; Dirac delta function; ping; voltage; pulse; sine wave; function; log decrement; damped harmonic oscillator; equation; Gnumeric; hertz; MHz; École Polytechnique Fédérale de Lausanne (Lausanne, Switzerland); IBM Research–Zurich (Rüschlikon, Switzerland); engineering; stress; ribbon; strain; material; silicon; transistor; frequency; semiconductor; solar cell; electron mobility; energy conversion efficiency; silicon nitride; etching (microfabrication); three-dimensional space; spatial; photonic crystal; deflection; flexural; stiffness; membrane; atto; newton (unit).